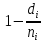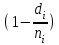3_курс_рус_Методология научного исследования. Доверительный интервал для доли 9
 Скачать 1.03 Mb. Скачать 1.03 Mb.
|
тема 4: Анализ выживаемостиАнализ выживаемости - статистический анализ, разработанный для изучения, оценки и сравнения времени, прошедшего до наступления некоторого события (появления метастазов, выздоровления, гибели, обострения заболевания). Выживаемость S(t) (Survive) – вероятность «прожить» время большее t с момента начала наблюдения. Термин впервые был введен страховыми агентами, которые оценивали продолжительность жизни. Е 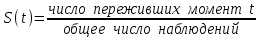 сли все наблюдения начались одновременно и закончились одновременно, то Таким образом, выживаемость – это вероятность ненаступления события до некоторого момента времени. События могут быть различные, не только нежелательные (гибель объекта), но и желательные – выздоровление, беременность при лечении от бесплодия, вступление в брак … Свойства функции S(t) S(t)=1, если t=0: в самом начале исследования ожидаемое событие не произошло ни у кого из наблюдаемых. Вероятность “дожития” до этого момента равна 1. S(t)=0, если t=∞: в конце исследования событие произошло у всех наблюдаемых. Вероятность “дожития” до этого момента = 0. График функции S(t)– кривая выживаемости отражает вероятность пережить любой из моментов времени t (рисунок 28). Время может измеряться в любых известных единицах (дни, месяцы и др). 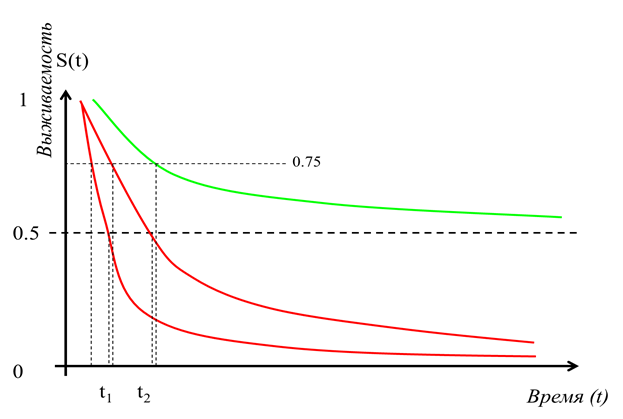 Рисунок 28 График может быть крутым, тогда говорят, что выживаемость низкая, т.е. ожидаемое событие наступило быстро у всех испытуемых. График может быть пологим, тогда выживаемость – высокая, т.е. потребовалось много времени, чтобы ожидаемое событие наступило у всех испытуемых. Кривая выживаемости используется, в частности, для определения медианы выживаемости и других процентилей времени жизни. Время, до которого доживет половина испытуемых, называется медианой выживаемости (Ме). Если событие не наступило у половины испытуемых вообще, то медиану определить невозможно, тогда определяют, время, до которого “дожили” (т.е. событие не наступило) три четверти всех испытуемых (75%). При сравнении двух кривых и более, по медиане можно оценить выживаемость в разных группах. Для построения кривой выживаемости необходимо одновременно начать наблюдение за всеми привлеченными к исследованию и всех «довести» до наступления события. Как правило, не все наблюдения начинаются одновременно, и не все заканчиваются одновременно, по разным причинам. Случается, что больной покидает больницу досрочно, или само исследование заканчивается до наступления события у данного конкретного участника, и мы не знаем, что с ним произошло в дальнейшем. Т.е. мы имеем дело с неполными (цензурированными) данными. Для построения кривой выживаемости по цензурированным данным используется метод Каплана-Майера. Предварительно строится так называемая таблица времени жизни.
Выживаемость рассчитывается как произведение по всем моментам времени, когда произошло хотя бы одно событие 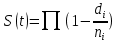 Как правило, не все наблюдения начинаются одновременно, и не все заканчиваются одновременно, по разным причинам. Случается, что больной покидает больницу досрочно и его дальнейшая судьба неизвестна. Т.е. мы имеем дело с неполными (цензурированными) данными. Для построения кривой выживаемости по цензурированным данным используется метод Каплана-Майера. Пример решения задачи (из книги Гланц Стентон. Медико-биологическая статистика, М:1999) Плутониане вообще живут недолго, что же будет теперь, когда Плутон охватила эпидемия пассивного курения! Первое, что мы должны сделать в этой ситуации, — это оценить продолжительность жизни плутонианина после начала пассивного курения. Вот как проводилось исследование. Мы попросили всех плутониан сообщать нам, как только в их домике появится активный курильщик. Выявленных таким образом пассивных курильщиков включали в группу наблюдения и дожидались (увы!) их смерти. Исследование длилось 15 плутонианских часов; за это время пассивными курильщиками стали 10 плутониан. Первыми сообщили о начале пассивного курения А и Б. Остальные участники вошли в группу наблюдения уже после начала исследования (что типично для исследований выживаемости); их звали В, Г, Д, Е, Ж, 3, И и К. Периоды наблюдения за каждым из них показаны на рис 11.1А в виде горизонтальных отрезков. Из десяти участников к концу исследования умерли семь — А, Б, В, Е, Ж, 3, К; в живых остались двое — Г и И. Еще одного участника, Д, местное начальство на 14-м часу исследования послало в командировку на Нептун; что с ни м было дальше, нам неизвестно. Таким образом, продолжительность жизни после начала пассивного курения нам известна в 7 случаях. В 3 случаях нам известно только, что наблюдаемые прожили не меньше такого-то срока*. Неважно, почему они не прослежены до конца жизни — всех их будем называть выбывшими. Б 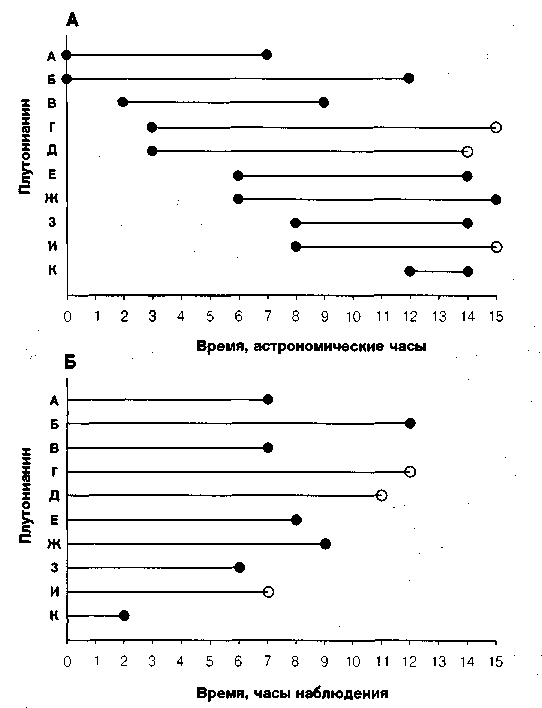 удем считать, что все начали наблюдаться в момент времени t=0, и от этого момента будем отсчитывать все сроки (рис. 11.1Б). Расположим плутониан по возрастанию длительности наблюдения (табл. 11.1) и укажем саму эту длительность во второй колонке таблицы. Длительность наблюдения, выбывших плутониан пометим знаком «+» - это будет означать, что плутонианин прожил более такого-то срока, а на сколько - неизвестно. Таблица 11.2. Расчет кривой выживаемости плутонианц после начала пассивного курения
Задачи для самостоятельного решения: Сравнить две кривые выживаемости. Сделать выводы.
Контрольные вопросы: Что понимается под термином «выживаемость»? Как строится кривая выживаемости по генеральной совокупности? Основные показатели кривой выживаемости? Какой метод используется для построения кривой выживаемости в случае неполных данных? Алгоритм построения кривой выживаемости по цензурированным данным? Практическое значение кривой выживаемости? Самостоятельная работа студентов | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||