11-14Вопросы_методы оптимальных решений. Двойственной или сопряженной
 Скачать 167.14 Kb.
|
|
Примерные вопросы к зачету по методам оптимальных решений 11.Двойственность в линейном программировании, экономическая интерпретация Каждой задаче линейного программирования соответствует другая задача, называемая двойственной или сопряженной по отношению к исходной. Теория двойственности оказалась полезной для проведения качественных исследований задач линейного программирования Предположим, что некоторая организация решила закупить ресурсы S1,S2,…,Sm предприятия и необходимо установить оптимальные цены на эти ресурсы y1,y2,…,ym. Покупающая организация заинтересована в том, чтобы затраты на все ресурсы Z в количествах b1, b2, bm пo ценам соответственно y1, y2, …,ym были минимальны, т.е Z=b1y1+b2y2+…+bmym стремиться к min С другой стороны, предприятие, продающее ресурсы, заинтересовано в том, чтобы полученная выручка была не менее той суммы, которую предприятие может получить при переработке в готовую продукцию. На изготовление единицы продукции Р1 расходуется а11 единиц ресурса S1, a21 единиц ресурса S2, ..., ai1 единиц ресурса S1, ..., аm1 единиц ресурса Sm по цене соответственно у1, y2, ..., уi, ..., уm . Поэтому для удовлетворения требований продавца затраты на ресурсы, потребляемые при изготовлении единицы продукции Р1, должны быть не менее ее цены c1 т.е. a11y1+a21y2+…+am1ym≥ c1 Аналогично можно составить ограничения в виде неравенств по каждому виду продукции. Экономико-математическая модель и содержательная интерпретация полученной таким образом двойственной задачи приведены в правой части табл. 6.1  12.Свойства двойственных оценок и их использование в анализе оптимального плана Теорема об оценках. Значения переменных yi * в оптимальном решении двойственной задачи представляют собой оценки влияния свободных членов bi в системе ограничений прямой задачи на величину целевой функции L(X* ):  Компоненты оптимального решения двойственной задачи yi * принято называть двойственными оценками. В экономике употребляется также термин «объективно обусловленные оценки». На свойствах двойственных оценок базируется экономикоматематический анализ распределения ресурсов. Свойство 1. Оценки как мера дефицитности ресурсов. Двойственные оценки отражают сравнительную дефицитность факторов производства. Чем выше величина оценки y j * , тем выше дефицитность j-го ресурса. Факторы, получившие нулевые оценки, не являются дефицитными и не ограничивают производство. Свойство 2. Оценки как мера влияния ограничений на значение целевой функции. Величина двойственной оценки какого-либо ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на единицу. Значение объективно обусловленной оценки называют теневой ценой ресурса. Теневая цена - это стоимость единицы ресурса в оптимальном решении. Однако нужно учитывать, что двойственные оценки позволяют измерить эффективность лишь незначительного изменения объема ресурсов. При значительных изменениях может быть получен новый оптимальный план и новые двойственные оценки. Свойство 3. Оценки как инструмент определения эффективности отдельных хозяйственных решений. С помощью двойственных оценок можно определить выгодность выпуска новых изделий, эффективность новых технологических способов производства. При этом эффективным может считаться тот вариант производства, для которого сумма прибыли, недополученной из-за отвлечения дефицитных ресурсов, будет меньше прибыли получаемой. Разница между этими величинами (Δj ) вычисляется как:  В том случае, если Δj ≤ 0, вариант производства является выгодным, если Δj > 0 – вариант невыгоден. Свойство 4. Оценки как мера относительной заменяемости ресурсов с точки зрения конечного эффекта. Например, отношение  показывает, сколько единиц k-го ресурса может быть высвобождено при увеличении объема i-го ресурса на единицу, для того чтобы максимум целевой функции остался на прежнем уровне; или наоборот, сколько единиц k-го ресурса необходимо дополнительно ввести при уменьшении на единицу объема i-го ресурса, если мы хотим, чтобы значение целевой функции не изменилось.Применение теорем двойственности позволяет, зная оптимальное решение одной из взаимно двойственных задач, найти оптимальное решение другой задачи. 13.Первая и вторая теоремы двойственности. Объективно обусловленные оценки и их смысл Теория двойственности в линейном программировании строится на двух основных теоремах. Теорема 1. Для прямой и двойственной задач в силе одно и только одно из следующих утверждений. 1. Если одна из задач линейного программирования имеет конечный оптимум, то и двойственная к ней задача также имеет конечный оптимум, причём оптимальные значения линейных форм обеих задач совпадают, т. е. Fmax = Zmin или Fmin = Zmax. 2. Если линейная форма одной из двойственных задач не ограничена, то условия другой задачи противоречивы. 3. Обе задачи не имеют решения, так как системы ограничений противоречивы. Теорема 2.Компоненты оптимального решения одной из задач (прямой или двойственной) равны абсолютным величинам коэффициентов при соответствующих переменных в выражении функции цели (линейной формы) другой задачи (двойственной или прямой) при достижении ею оптимума и при условии, что полученное оптимальное решение не является вырожденным. Из теорем 1 и 2 следует, что если решить одну из взаимно двойственных задач линейного программирования, то есть найти её оптимальное решение и оптимум функции цели, то можно записать оптимальное решение и оптимум функции цели другой задачи. Теперь пример, который поможет разложить всё вышеизложенное по полочкам. Компоненты оптимального решения двойственной задачи называются оптимальными оценками исходной задачи или (по версии академика Л.В. Канторовича) объективно обусловленными оценками - ООО. объективно обусловленные оценки ресурсов определяют степень дефицитности ресурсов: по оптимальному плану производства дефицитные (т.е. полностью используемые) ресурсы получают ненулевые оценки, а недефицитные – нулевые оценки. ООО ресурсов позволяют судить об эффекте лишь при достаточно малых изменениях bi, т.к. в противном случае может произойти переход в другую угловую точку, соответствующую другому оптимальному решению. 14. Экономико-математическая модель транспортной задачи Важным частным случаем задачи линейного программирования является так называемая транспортная задача. Классическая транспортная задача – задача о наиболее экономном плане перевозок однородного продукта (или взаимозаменяемых продуктов) из пунктов производства в пункты потребления. Экономико-математическая модель транспортной задачи в общем виде может быть сформулирована следующим образом: Имеется m пунктов производства однородного продукта и n пунктов потребления. Для каждого пункта производства i задан объем производства Аi, для каждого пункта потребления j известна потребность (спрос) Вj (в тех же единицах измерения). Известны издержки сij, связанные с перевозкой единицы продукта из пункта i в пункт j. Требуется составить план перевозок, обеспечивающий наиболее экономным путем (т.е. при наименьших транспортных издержках) удовлетворение всех пунктов потребления за счет реализации всего продукта, произведенного пунктами производства. При этом предполагается, что суммарный спрос (В=åjВj) равен суммарному объему производства (А=åiАi). Такие задачи называются закрытыми транспортными задачами. Система ограничений примет вид  = Аi (i=1,2,…,m), (2.3.1) = Вj (j=1,2,…n). (2.3.2)Система (2.3.1) включает в себя уравнения баланса по поставщикам, а система (2.3.2) – по потребителям. Суммарные транспортные издержки выражаются в виде следующей линейной функции, которую необходимо минимизировать F = 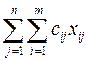 à min (2.3.3)Математическая модель транспортной задачи в общей постановке будет следующей: на множестве неотрицательных решений системы ограничений (2.3.1), (2.3.2) (мы будем называть такие решения допустимые) найти такое решение Х=(х11, х12,…,хij ,…,хmn), при котором значение целевой функции (2.3.3) минимально. Условия транспортной задачи весьма удобно представлять в табличной форме. 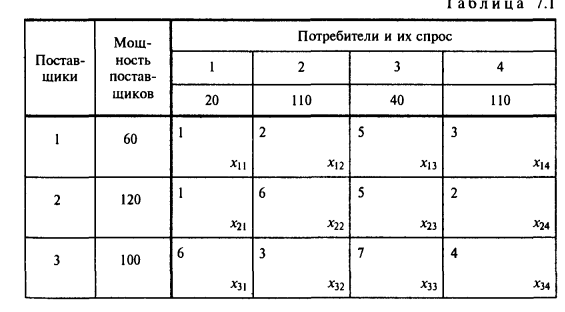 В левом верхнем углу произвольной клетки (i,j) (i – номер строки, j–номер столбца) стоит показатель транспортных затратсij,в правом нижнем – значения переменных хij(план перевозок). Любое решение Х=(х11, х12,…, хij ,…, хmn) системы ограничений (2.3.1) – (2.3.2) назовем распределением поставок.
|