Двухпроводные направляющие системы. Двухпроводные направляющие системы
 Скачать 123.11 Kb.
|
|
, а параметры G и C (поперечные) суммарную проводимость 
. Из указанных четырех первичных параметров кабеля лишь R и G обуславливаю потери энергии первый - потери на тепло в ТПЖ и других металлических частый кабеля (экран, оболочка, брони), второй - потери в изоляции.| |
Рассмотрим однородную кабельную цепь с первичными параметрами R, L, C и G
В начале цепи включен генератор сопротивлением Z0 в конце нагрузка ZL. Обозначим напряжение и ток в начале цепи U0, I0, в конце UL, IL.
Выделим на расстоянии x от начала цепи бесконечно малый участок dx. Обозначим силу тока, протекающего по элементу цепи dx, через I и напряжение между проводниками через U. Тогда падение напряжения на dx будет:
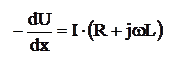(1)Знак минус перед производными в левой (1) части уравнений означает, что U и I с увеличением x уменьшаются. Утечка тока на участке dx:
(2)Для решения этих уравнений относительно U и I исключим сначала I из (1), взяв вторую производную:
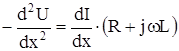
Подставим это выражение в (2) и получим:
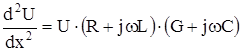(3)обозначим:
тогда:
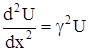
Решение этого уравнения имеет вид:
дифференцирую это уравнение, получим выражение для тока:
Подставив это выражение в (1), получим:
или, обозначив
(5)имеем:
Таким образом, имеем два уравнения с двумя неизвестным А и В:
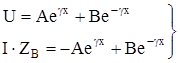(6)Для нахождения постоянных А и В воспользуемся значениями тока и напряжения в начале цепи (при x=0) I0 и U0. Тогда (3.1.6) примут вид:
отсюда:
(7)подставив значение А и В в (6), получаем:
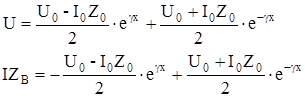
Производя соответствующие преобразования и с учетом того, что:
получим значения напряжения Ux и тока Ix в любой точке цепи:
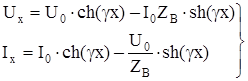(8)В конце цепи при x = L получим:
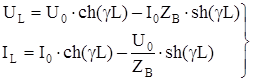(9)Практически, оказывается, удобно пользоваться выражениями, устанавливающими зависимость напряжения и тока вначале цепи от напряжения и тока в конце цепи.
Решив (9) относительно U0 и I0 получим:
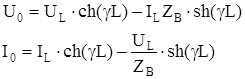(10)Уравнения (8) – (10) устанавливают взаимосвязь токов и напряжений с параметрами цепи R, L, C и G или Y и ZB, позволяя определить напряжение и ток в любой точке цепи в зависимости от значений U и I в начале или в конце. Эти уравнения справедливы при любых нагрузках Z0 и ZL по концам цепи.
При согласованных нагрузках (Z0=ZL=ZB) U0 /I0=UL/IL=ZB уравнения (8)–(10) упрощаются и принимают вид:
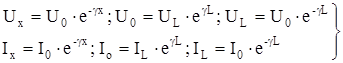(11)Практически наиболее часто пользуются уравнениями в виде:
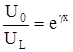и 
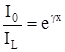(12)В этом случае отношение мощностей в начале и конце линии имеет вид:
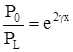(13)Таким образом, получены уравнения однородной кабельной цепи в общем, виде при любых нагрузках по концам, формулы: (8) – (10), и при согласованных нагрузках, формулы: (11) – (13).
Из приведенных формул следует, что распространение энергии по линии, ток и напряжение в любой точке цепи обусловим двумя параметрами Y и Zв.
3.2 Вторичные параметры двухпроводных
направляющих систем
Вторичными параметрами линии являются сопротивление Zв и коэффициент распространения Y. Они широко используются для оценки эксплуатационно-технических качеств линии связи. При проектировании, сооружении и эксплуатации кабельных линий в первую очередь корректируются и контролируются именно вторичные параметры линии.
3.2.1 Волновое сопротивление Zв
Это сопротивление, которое встречает электромагнитная волна при распространении вдоль однородной линии без отражения, т.е. при условии отсутствия внимания на процесс передачи несогласованности нагрузок по концам линии; Zв свойственно данному типу кабеля и зависит лишь от его первичных параметров и частоты передаваемого тока.
Количественное соотношение, имеющие место между волной напряжения и волной тока в линии, и есть волновое сопротивление цепи. При этом, как следует из данного определения волнового сопротивления, необходимо рассматривать лишь падающую (движущуюся вперед) электромагнитную волну:
Если в линии выделить отдельно отраженную волну, то она, двигаясь к началу линии, также будет встречать сопротивление, равное волновому:
Волновое сопротивление рассчитывается по формуле:
По всей физической природе, что также следует и из приведенной формулы, значение Zв не зависит от длины кабельной линии и постоянно в любой точке цепи.
В общем виде волновое сопротивление является комплексной величиной и может быть также выражено через его действительную и мнимую части:
на практике величину волнового сопротивления оговаривают в ГОСТе, при этом величина Zв по длине должна быть одинаковой, то поскольку практически не выполнимо то в ГОСТе задаются пределы
, пример 
Oм.3.2.2 Коэффициент распространения
Электромагнитная энергия, распространяясь вдоль кабельной линии, уменьшается от начала к концу линии. Уменьшение, или затухание, энергии объясняется потерями её в цепи передачи. Следует различать два вида потерь энергии. Во-первых, потери в металлических элементах кабеля и во-вторых, потери в изоляции.
Потери в цепи передачи учитываются через коэффициент распространения Y, который является комплексной величиной и м.б. представлен суммой действительной и мнимой её частей:
Тогда уравнение для тока и напряжение можно представить в следующем виде:
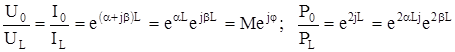
Модуль этого выражения
характеризует уменьшение абсолютного значения тока или напряжение при прохождении по линии длиной L. Угол 
характеризует изменение угла векторов тока или напряжение на этом же участке линии длиной L.При передаче сигналов связи параметры a и b характеризуют соответственно затухание и изменения фаз тока, напряжения и мощности на участке кабельной цепи длиной 1 км и называются коэффициентом затухания и коэффициентом фазы.
Логарифмируем обе части приведенных выше выражений, получаем формулы для расчета затухания:
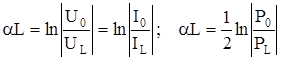
Затухание цепи связи (a=aL) принято оценивать в неперах (Нп) или децибелах (дб). Для неперов используется натуральная система логарифмов, а для децибелов (бело) -десятичная. Затухание в 1 Нп соответствует уменьшение мощностей
раза, а для U или I в 
раза.Это вытекает из:
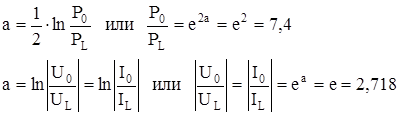
Затухание в 1 дБ характеризует уменьшение по мощности в 1.26 раз, а по току или напряжению в 1.12 раза:
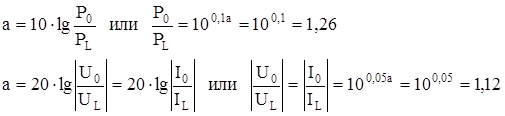
Между неперами и децибелами существует следующее соотношение:
|
т.е.
На рис.2. показан характер изменения тока вдоль однородной кабельной линии. Как видно из графика, вектор тока уменьшается и изменяет фазу вдоль линии. Уменьшение тока происходит по экспоненциальному закону.
Рассмотрим зависимость вторичных параметров кабельной линии от частоты. Для упрощенного анализа этой зависимости выразим вторичные параметры кабельных линий Zв и Y сокращенными формулами, которыми можно пользоваться для расчетов.
При постоянном токе (f=0):
В диапазоне низких частот (f=800 Гц) учитывая, что индуктивность кабельных цепей невелика, в указаном частном диапазоне пренебрегаем значением wL по сравнению с R. В этом случае можно также не считаться с параметром G по сравнению с wС, т.е. в низкочастотном диапазоне R>wL и G>wC, тогда:
Следовательно:
В свою очередь:
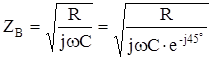
Выразим a и b через первичные параметры передачи R, L, G и C:
отсюда:
можно записать, что
отсюда:
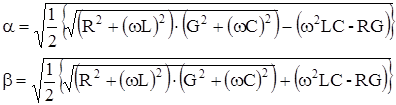
При высоких частотах (> 60 Кгц), когда
формула для a и b может быть упрощена, для этого запишем:
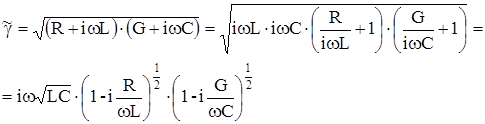
Раскладывая двучлены, заключенные в скобки, в биноминальные ряды:
и в силу малости x ограничиваясь только двумя первыми членами, ряда и пренебрегая малыми членами, запишем:
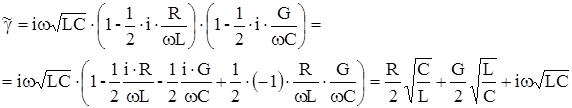
Откуда:
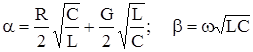
В диапазоне высоких частот 30 Кгц и выше. При высококачественной передаче по кабельной цепи имеют место следующие соотношения:
Тогда, применив к выражению g формулу бинома Ньютона, и ограничившись первыми 2-мя членами разложения, получим:
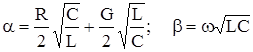
Волновое сопротивление в этом случае можно рассчитывать по формуле:
