Эффективное кодирование. Эффективное кодирование дискретных сообщений
 Скачать 292 Kb. Скачать 292 Kb.
|
|
Лабораторная работа по дисциплине: «Теория информации» Тема: «Эффективное кодирование дискретных сообщений» Цель работы: Изучение методов эффективного кодирования дискретных сообщений в отсутствии помех и освоение способов практической реализации этих методов на ЭВМ. Теоретическая часть. Задачи эффективного кодирования заключаются в следующем: Запоминание максимального количества информации в ограниченной памяти. Обеспечение максимальной пропускной способности источника сообщений. Максимальное количество информации I, которое может передаться сигналом, определяется по формуле. где mу - количество состояний сигнала. Фактический объем переносимой информации определяется энтропией его множества сообщений Н. В связи с тем, что в основном в передаваемом наборе сообщений присутствуют типичные последовательности, сообщения передаются с относительной избыточностью D. Для уменьшения избыточности символов необходимо применить эффективное кодирование. Эффективным называется способ кодирования, при котором: Не возникает потери информации. Требуется минимальное количество кодовых символов. Для выполнения второго условия используются неравномерные коды, где длина кодового слова обратно пропорциональна вероятности его появления в сообщении. Использование эффективного кодирования целесообразно, если вероятности появления различных букв существенно различаются, так как при этом энтропия множества букв (блоков) существенно меньше их информационной емкости. Эффективное кодирование достигается благодаря учету априорных статистических характеристик источника информации. Предельные возможности эффективного кодирования определяются: Для оценки эффективности неравномерных кодов используется коэффициент относительной эффективности Кэ=Н/nср Результаты расчета. Для расчетов примем вероятность появления ‘1’ равной 0.3 Метод Шеннона-Фано. Алгоритм метода Шеннона-Фано — один из первых алгоритмов сжатия, который впервые сформулировали американские учёные Шеннон и Фано. Алгоритм основан на частоте повторения. Так, часто встречающийся символ кодируется кодом меньшей длины, а редко встречающийся — кодом большей длины. В свою очередь, коды, полученные при кодировании, префиксные. Это и позволяет однозначно декодировать любую последовательность кодовых слов. Основные этапы: Символы первичного алфавита m1 выписывают по убыванию вероятностей. Символы полученного алфавита делят на две части, суммарные вероятности символов которых максимально близки друг другу. В префиксном коде для первой части алфавита присваивается двоичная цифра «0», второй части — «1». Полученные части рекурсивно делятся, и их частям назначаются соответствующие двоичные цифры в префиксном коде. Расчет:
Средние длины слов: 1.712 Коэффициент эффективности: 1.02
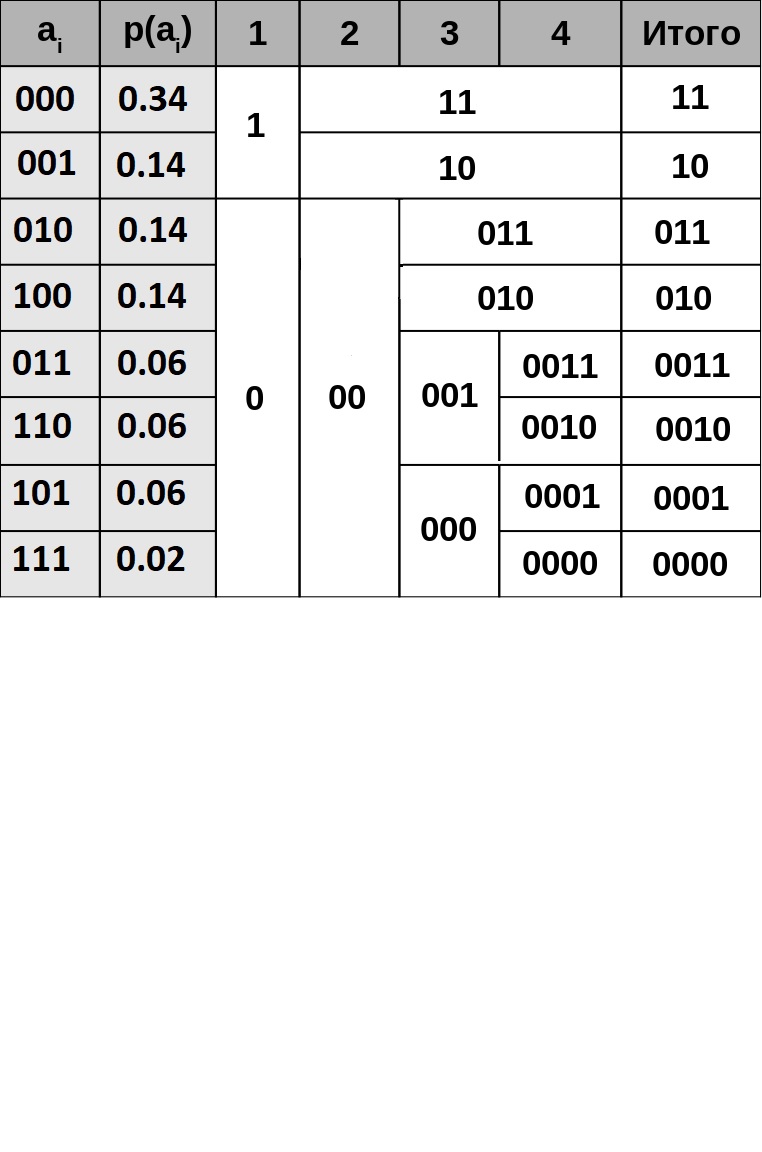 Средние длины слов: 2.525 Коэффициент эффективности:1.04
Средние длины слов: 3.363 Коэффициент эффективности: 0.92 Метод Хаффмана. Метод Хаффмана - статистический метод сжатия, который уменьшает среднюю длину кодового слова для символов алфавита. Код Хаффмана является примером кода, оптимального в случае, когда все вероятности появления символов в сообщении - целые отрицательные степени двойки. Код Хаффмана может быть построен по следующему алгоритму: Выписываем в ряд все символы алфавита в порядке возрастания или убывания вероятности их появления в тексте; Последовательно объединяем два символа с наименьшими вероятностями появления в новый составной символ, вероятность появления которого полагается равной сумме вероятностей составляющих его символов; в конце концов мы построим дерево, каждый узел которого имеет суммарную вероятность всех узлов, находящихся ниже него; Прослеживаем путь к каждому листу дерева помечая направление к каждому узлу (например, направо - 1, налево Расчет:
Средние длины слов: 1.81 Коэффициент эффективности: 0.96
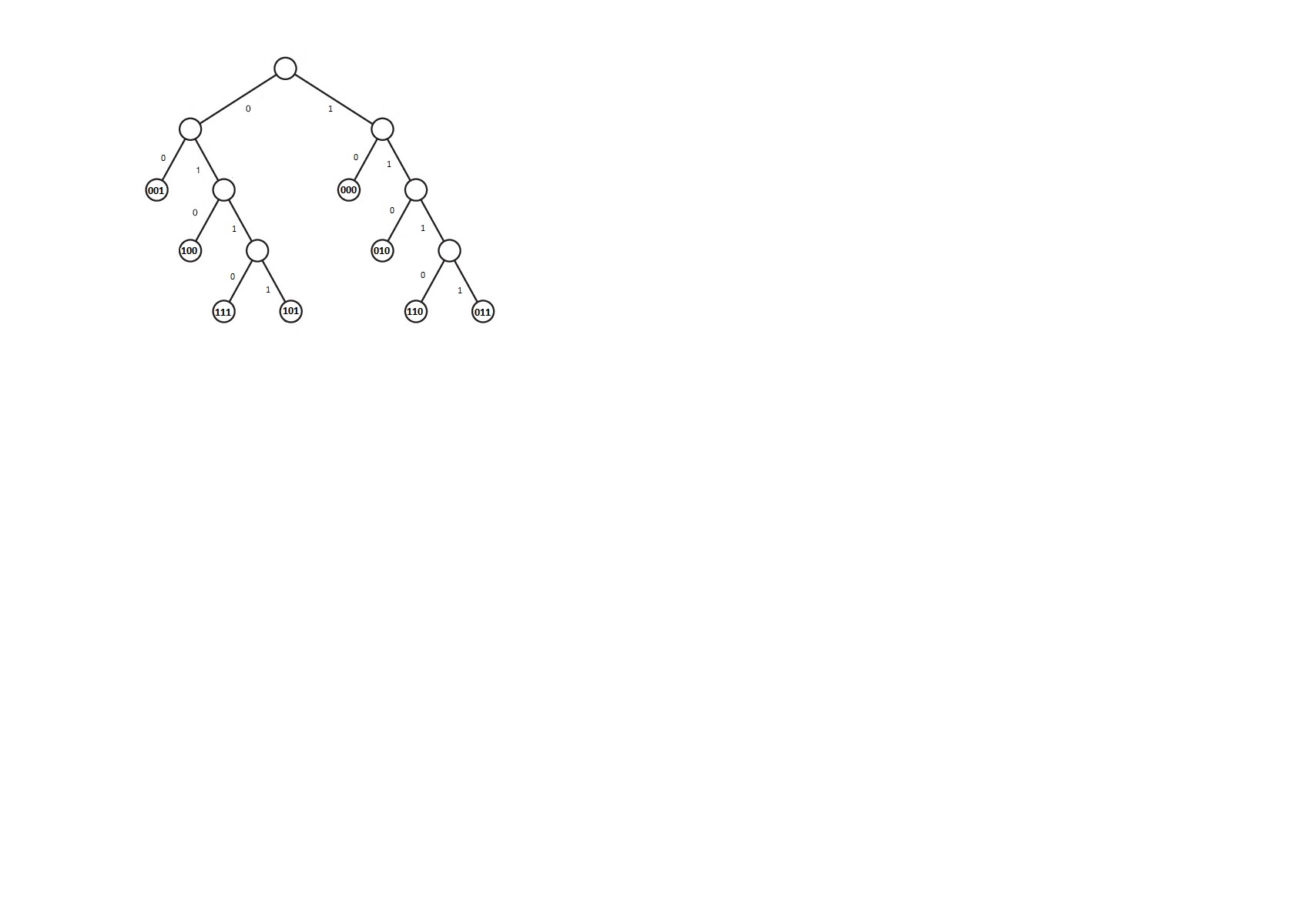 Средние длины слов: 2.525 Коэффициент эффективности: 1.04
Средние длины слов: 3.11 Коэффициент эффективности: 1 Анализ данных: При n=2: - энтропия - 1.75 - максимальное количество информации – 0.6 -информация на символ – 0.3 -энтропия на символ – 0.875 При n=3: - энтропия – 2.64 - максимальное количество информации – 0.9 -информация на символ – 0.3 -энтропия на символ – 0.88 При n=4: - энтропия – 3.11 - максимальное количество информации – 1.2 -информация на символ – 0.3 -энтропия на символ – 0.77 Выводы по работе В данной работе исследовались способы эффективного кодирования информации с использованием методик Шеннона-Фано и Хаффмена и применение их в системах сжатия данных. Проанализировав полученные при выполнении работы результаты, необходимо отметить следующее: Методика Шеннона-Фано не гарантирует однозначности построения кода, поскольку при разбиении таблицы вероятностей на подгруппы возможны разные варианты разбиения. Методика Хаффмена менее подвержена этому недостатку и гарантирует большую однозначность построения кода с наименьшим числом символов на букву алфавита сообщения при заданном распределении вероятностей, чем и обусловлено его применение во многих известных архиваторах. Из сравнения длин кодовых слов данных по методам Шеннона-Фано и Хаффмена следует, что метод Хаффмена во всех случаях дает коэффициент сжатия лучший, чем метод Шеннона-Фано. Это вызвано уже упоминавшейся неоднозначностью разбиения на группы при кодировании с использованием метода Шеннона-Фано. Общим и очевидным недостатком применения неравномерных оптимальных кодов (в т.ч. Шеннона-Фано и Хаффмена) является снижение надежности передачи и хранения информации, т.к. в случае искажения или потери хотя бы одного бита кодовой комбинации при декодировании будет потеряна не только текущая (декодируемая) буква, но и все последующие буквы исходного сообщения. Контрольные вопросы: Почему используется логарифмическая мера информации? При измерении величина может принимать значений. Чем больше , тем труднее определить ее истинное (действительное) значение. Следовательно, исходная неопределенность возрастает с увеличением . Исходная неопределенность до измерения определяется логарифмической функцией от , то есть: Единицы неопределенности определяются выбором основания логарифма. При а2 двоичная единица информации или бит, а2 при – десятичная. Достоинством логарифмической меры является удобство при описании (обработки) сложных опытов, так как она удовлетворяет требованию аддитивности. Какие последовательности называются типичными? Последовательности, для которых выполняется равенство Ni=pi*n, называются типичными. Согласно закону больших чисел при росте n все большее число последовательностей становятся типичными, а в пределе, при Вероятность появления любой типичной последовательности вычисляется по одной и той же формуле: 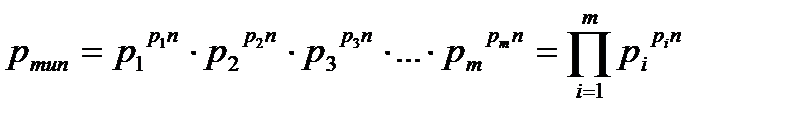 где m – число букв в алфавите (объем алфавита). От каких характеристик регистра зависит неопределённость (энтропия) его состояния? Энтропи́я (информационная) — мера хаотичности информации, неопределённость появления какого-либо символа первичного алфавита. При отсутствии информационных потерь численно равна количеству информации на символ передаваемого сообщения. Информационная энтропия для независимых случайных событий x с n возможными состояниями (от 1 до n) рассчитывается по формуле: 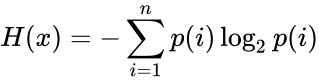 Таким образом, энтропия события x является суммой с противоположным знаком всех произведений относительных частот появления события i, умноженных на их же двоичные логарифмы (основание 2 выбрано только для удобства работы с информацией, представленной в двоичной форме). Это определение для дискретных случайных событий можно расширить для функции распределения вероятностей. Почему энтропия, рассматриваемая, как количество информации при-ходящееся на один разряд, может быть меньше одного бита? Так как 0 J(a) кол-во информации Каким параметром системы (источника сообщений) определяется мак-симальное значение энтропии? Энтропия принимает максимальное значение в случае когда вероятность всех событий одинакова. В каком случае определения количества информации по К. Шеннону и по Хартли совпадают? В каком случае определения количества информации по К. Шеннону и по Хартли совпадают? Формула Шеннона дает оценку информации независимо, отвлеченно от ее смысла: 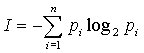 где n - число состояний системы; рi - вероятность (или относительная частота) перехода системы в i-е состояние, причем сумма всех pi равна 1. Если все состояния равновероятны (т.е. рi=1/n ), то I=log2n. Для случая равномерного закона распределения плотности вероятности мера Шеннона совпадает с мерой Хартли. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
