ВКР ДРАНИЧКИНА ЕЛЕНА. Экранной изоляции

• Название: Экранной изоляции
• Анкор: ВКР ДРАНИЧКИНА ЕЛЕНА
• Дата: 09.11.2022
• Размер: 0.79 Mb.
• Имя файла: VKR_Dranichkina_11324095.docx
• Тип: Обзор; #778873
• страница: 12 из 16



w– скорость воздуха в воздуховоде, м/с;

v – коэффициент кинематической вязкости воздуха, м²/с;

коэффициент теплопередачи изолированного воздуховода kдля данного случая будет определяться по формуле


k ¹

1 _ ^2

₁ ₂

_1

_н

Вт/(м²·ºС),

где

^_н- коэффициент теплообмена на наружной поверхности изолированного

воздуховода, Вт/(м²·ºС).

^{н к  л}, (2.46)

где ^_к

и ^{ л}

- коэффициенты конвективного и лучистого теплообмена на

поверхности изолированного воздуховода, Вт/(м²·ºС).

Согласно [28]

^{Nuн 0,695 Gr0.25} , (2.47)

^{  Nuнв} . (2.48)

к _d

экв
Коэффициент лучистого теплообмена определяется по формуле

^_ t 273_⁴

_ t  273_^{4 }

^из^CO <sup>в 

 п </sup> 

 _л

_

100

t_в

 

• 
  t_п
  

100

^{ } , (2.49)

где

_из- степень черноты поверхности изоляционного слоя,

_из 0,04 ;

^t_п- температура поверхности изолированного воздуховода, ºС:

в
t_п t^н

t t^н1

в

• 
  в
  

(

R_о _в

 _{ i1} R)_,

R_о - сопротивление теплопередаче изолированного воздуховода,

(м²·ºС)/Вт, определяется по формуле

1


R_о

в

• 
  _ R_i
  

_ 1 _,

_н

где

_в
Nu_в <sub>f

d</sub> .

экв
В результате расчета получаем, что среднее повышение температуры транспортируемого воздуха на 1 м длины изолированного воздуховода при заданных исходных данных составило 0,07 ºС/м.

В работах [26, 27] отмечается, что применение невентилируемой воздушной прослойки может существенно повысить теплозащитные свойства утепляемых конструкций.

Рассмотрим вариант прокладки воздуховодов, утепленных с применением экранной тепловой изоляции и невентилируемой воздушной прослойки, при аналогичных условиях. Схема выше указанной конструкции воздуховода представлена на рис. 2.7.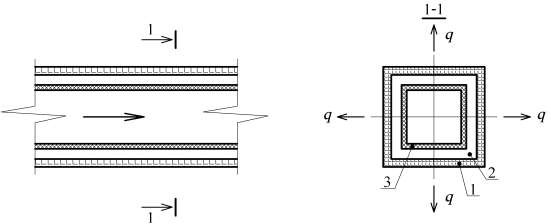




Рис. 2.7. Схема конструкции воздуховода, утепленного с применением экранной тепловой изоляции и воздушной невентилируемой прослойки

1 – экранная теплоизоляция; 2 – воздушная прослойка; 3 – металлический воздуховод

Толщина воздушной прослойки δ_впринята равной 10 мм, теплопроводность λ_эквзамкнутой экранированной воздушной прослойки определялась по методике, изложенной в п. 2.1.

По результатам расчета среднее повышение температуры транспортируемого воздуха на 1 м длины изолированного воздуховода в этом случае при заданных исходных данных составило 0,028 ºС/м.

Результаты расчета изменения температуры транспортируемого воздуха представлены на рис. 2.8.




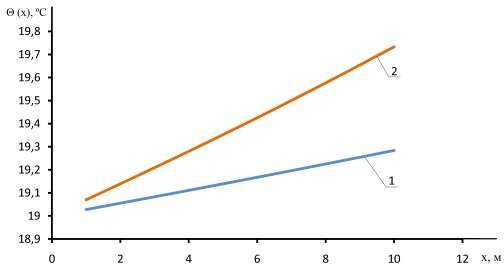
Рис. 2.8. Результаты расчета повышения температуры транспортируемого воздуха: 1 – для конструкции воздуховодов с замкнутой воздушной

прослойкой; 2 – для конструкции воздуховодов без замкнутой воздушной прослойки

Результаты расчета также представлены в виде зависимости (рис. 2.9)

безразмерной температуры  от безразмерной координаты
безразмерной температуры ^ определяется выражением

^l . Значение

^dэкв

  ^{0  l}, (2.50)

₀  t_н

где _l– температура транспортируемого воздуха в конце участка.

Рассмотрим вариант прокладки воздуховодов на открытом воздухе. В этом случае будем определять понижение температуры транспортируемого воздуха.

При расчете принимаются следующие исходные данные:

температура наружного воздуха t_н=-30 ºС, принимается по СП 131.13330.2012 «Строительная климатология»;

максимальная из средних скоростей ветра за январь υ_н=5,4 м/с, принимается по [102];

в
температура воздуха, поступающего в воздуховод t^н ₀

 25С;

исходные данные для конструкций воздуховодов, представленных на рис.

2.6 и 2.7, такие же, как и в предыдущем варианте.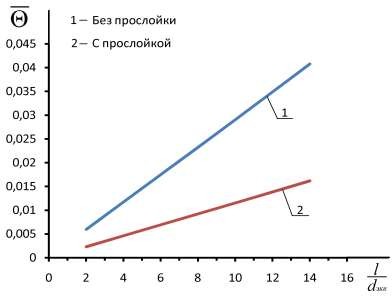




Рис. 2.9. Зависимость изменения температуры транспортируемого воздуха по изолированному воздуховоду, проложенному в помещении: 1 – для конструкции воздуховодов с замкнутой воздушной прослойкой; 2 – для

конструкции воздуховодов без замкнутой воздушной прослойки
В результате расчета при заданных исходных данных среднее понижение температуры транспортируемого воздуха на изолированном участке воздуховода, утепленного экранной тепловой изоляцией без воздушной прослойки, составило 0,56 ºС/м. Среднее понижение температуры транспортируемого воздуха на изолированном участке воздуховода,

утепленного экранной тепловой изоляцией с воздушной прослойкой, составило 0,24 ºС/м.

На рис. 2.10-2.11 представлены результаты расчета изменения температуры транспортируемого воздуха в размерных и безразмерных координатах для воздуховода, проложенного на открытом воздухе.



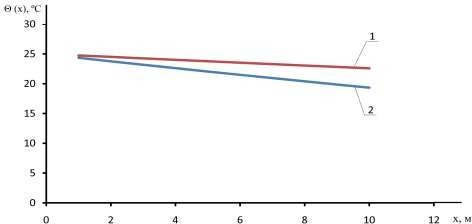
Рис. 2.10. Результаты расчета понижения температуры транспортируемого воздуха: 1 – для конструкции воздуховодов с замкнутой воздушной

прослойкой; 2 – для конструкции воздуховодов без замкнутой воздушной прослойки



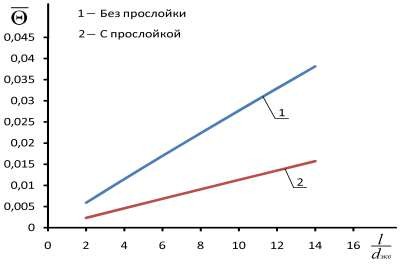
Рис. 2.11. Зависимость изменения температуры транспортируемого воздуха по изолированному воздуховоду, проложенному снаружи: 1 – для конструкции воздуховодов с замкнутой воздушной прослойкой; 2 – для

конструкции воздуховодов без замкнутой воздушной прослойки
С физической точки зрения безразмерная температура  представляет собой эффективность теплообмена между транспортируемым воздухом и воздухом окружающей среды. Графические зависимости, представленные на рис. 2.9 и 2.11, показывают, что эффективность теплообмена увеличивается по длине начального участка. Однако очевидной остается эффективность применения невентилируемой воздушной прослойки при утеплении воздуховода.

2. 
   Математическое моделирование процесса стационарного теплообмена в ограждающих конструкциях длинных воздуховодов
   

Изложенная в п. 2.2.1 расчетная методика применима для коротких каналов (воздуховодов), для которых местный коэффициент теплоотдачи способен изменяться в 2 раза и более.

Для длинных воздуховодов (длиной

l^dэкв

 50) поправка, учитывающая

изменения среднего коэффициента теплоотдачи,

_l 1. В этом случае тепловой

расчет ограждающих конструкций воздуховодов возможно производить при постоянном коэффициенте теплопередачи.

В связи с этим на решение задачи стационарного теплопередачи через ограждающие конструкции воздуховодов можно распространить метод безразмерных характеристик, разработанный В. М. Кейсом и А. Л.Лондоном [55]. Данный метод основывается на использовании критериев эффективности рекуперативных теплообменных аппаратов ε и безразмерного числа переноса тепла NTU.

Рассмотрим повышение температуры при движении воздуха в воздуховоде

длиной, превышающей длину начального термического участка (

l^dэкв
 15),

утепленного с помощью экранной изоляции. Условия для расчета примем аналогичные условиям, рассматриваемым в п. 2.2.1.

График изменения температур транспортируемого воздуха по длине воздуховода и воздуха внешней окружающей среды представлен на рис. 2.12.

Температура t_в

соответствует температуре воздуха в помещении, температуры

t

и

в в

t
^нкравны температурам транспортируемого воздуха в начале и в конце
рассматриваемого участка воздуховода соответственно.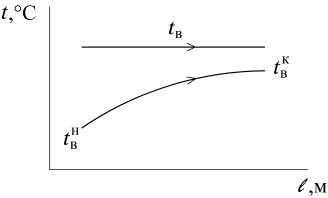



Рис. 2.12. График изменения температур транспортируемого воздуха по длине воздуховода, прокладываемого в помещении, и воздуха внешней окружающей среды

Эффективность теплообмена εв данном случае определяется по формуле:
t^к t<sup>н

εв в</sup>. (2.51)


в
t_в t^н
Согласно [55] выражение (2.51) можно записать в следующем виде

ε 1 e^NTU

, (2.52)

где NTU – безразмерное число единиц переноса тепла, определяется по формуле

NTU

^{ k Fиз} , (2.53)

с_в G_в

^kкоэффициент теплопередачи изолированного воздуховода, Вт/м²·ºС, определяется по формуле
^{k 1} . (2.54)