ВКР ДРАНИЧКИНА ЕЛЕНА. Экранной изоляции

• Название: Экранной изоляции
• Анкор: ВКР ДРАНИЧКИНА ЕЛЕНА
• Дата: 09.11.2022
• Размер: 0.79 Mb.
• Имя файла: VKR_Dranichkina_11324095.docx
• Тип: Обзор; #778873
• страница: 2 из 16



i0

(i1 )m



i0 _i

(i1 )m

где F₀ и F_m– площади поверхностей источника тепла или теплоприемника;
t₀ и t_m– температуры поверхностей источника тепла и теплоприемника;
¹ – суммарный коэффициент теплопередачи, который определяется как

_i

сумма теплоотдачи α_лiи теплопроводностью α_сi;
Z– количество экранов;

_{(i1 )m}^{– коэффициент облученности, равный Fm/Fi+1.}
Исследование конвективной составляющей в процессе теплопереноса через замкнутую воздушную прослойку, разделенную листами стальфолевой изоляцией с дистанцией 2-5 мм при давлении Pот 98 до 4600 кПа, описано в работе [20].

В рассматриваемом случае передача тепла осуществлялась путем теплопроводности и конвекции (λ_к), излучением (λ_л), а через материал экранов и дистанцирующих прокладок – путем теплопроводности материала (λ_м). Величина теплопроводности материала λ_мопределялась по [19]. При известной мощности нагревателя и температурном перепаде в слое определялась эффективная теплопроводность:

_эф _к(_л _м). (1.8)
Суммарное значение величин λ_л и λ_м определялось в ходе работы [21] для каждого образца при рабочей разности температур Δt и атмосферном давлении в случае, когда λ_л= λ_г, где λ_г – коэффициент теплопроводности газа.

В литературе [7] предлагается коэффициент теплообмена при свободной конвекции уменьшать вдвое, т.к. при передаче теплоты с помощью конвекции от одной поверхности замкнутой воздушной прослойки к другой происходит преодоление сопротивления двух пограничных слоев воздуха, которые прилегают к этим поверхностям. Тогда тепловой поток Q, проходящий через прослойку можно выразить следующим образом:

Q 0,5<sub>к

</sub> _л



 _л
, (1.9)

где α_к– коэффициент конвективного теплообмена; δ – толщина прослойки;

λ – коэффициент теплопроводности воздуха;

λ_л– коэффициент лучистого теплообмена.
Результаты исследований представлены в работе [23] в виде зависимости коэффициента конвекции ε_кот Gr∙Pr для вертикальных и горизонтальных газовых прослоек.

В работе [28] рассматривается процесс передачи теплоты через замкнутые газовые прослойки, где также учитывается влияние естественной циркуляции среды в ограниченном пространстве. При этом учитывается взаимное расположение нагретых и холодных поверхностей, а также расстояние между ними.

Для упрощения расчетов сложный процесс теплообмена рассматривается как элементарное явление теплопроводности. При этом вводится понятие эквивалентного коэффициента теплопроводности, которая определяется из выражения:

^эк

_Q

Ft
. (1.10)

Коэффициент конвекции ε_кравен отношению эквивалентного коэффициента теплопроводности λ_экк коэффициенту теплопроводности среды λ. Поскольку циркуляция обусловлена разностью плотностей холодных и нагретых частиц и зависит от произведения Gr и Pr, то величина ε_ктакже является функцией того же аргумента, т.е.

_к

^{f(Gr  Pr )}.

При определении численных значений Gr и Pr в качестве определяющего размера принимается толщина воздушной прослойки δ, а определяющая температура среды определялась как средняя температура:

t_ср 0,5t₁  t₂ , (1.11)

где t₁ и t₂ – температуры нагретой и холодной стенок.
При Gr∙Pr менее 1000 значение величины ε_к=1. В этом случае теплоперенос через воздушную прослойку осуществляется только путем теплопроводности ограниченной среды и излучением.

При значениях 10³6

_к 0,105(Gr  Pr )^0,3

. (1.12)

Для приближенных расчетов ε_кпри GrPr>10³ вместо формулы (1.12) М. А. Михеев рекомендует на основании данных [24] использовать следующую зависимость

_к 0,18(Gr Pr )^0,25

, (1.13)

которую можно привести к виду
_к
 A(  t)^0,25

, (1.14)

где

A 0,18
(  g Pr )^0,25

_0,5 ^,

где β – температурный коэффициент объёмного расширения; g – ускорение свободного падения;

v– коэффициент кинематической вязкости.
В работе также приведена графическая зависимость ε_кот GrPr, которая наглядно показывает результаты опытных данных и вышеприведенной расчетной обработки. Как видно из рис. 1.1, несмотря на условность обработки и выбора определяющих параметров, точки, полученные в [25], для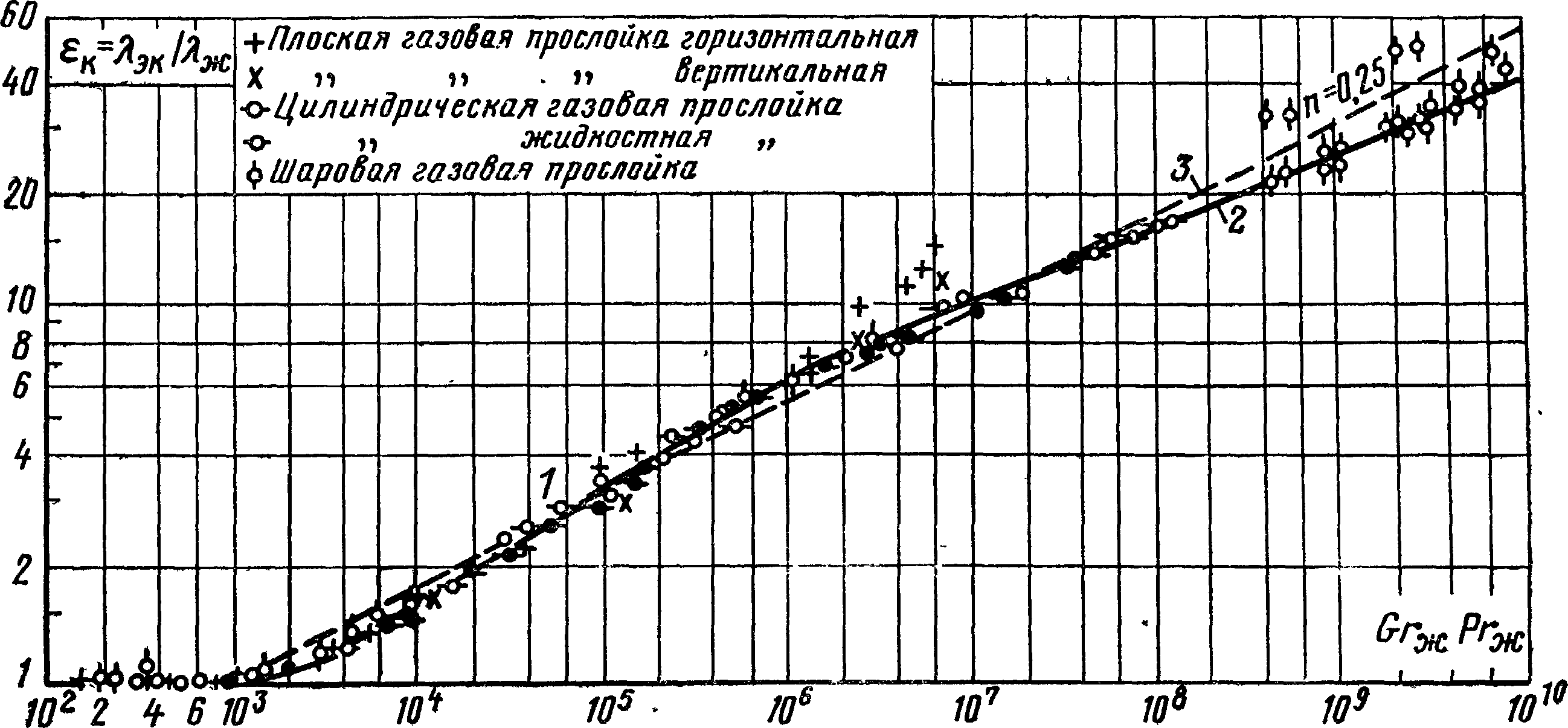

плоских, цилиндрических и шаровых прослоек довольно хорошо укладываются на одну общую кривую.
Рис. 1.1. Зависимость ε_к=f(GrPr) при естественной циркуляции в замкнутом

пространстве
Васильев, Б. Ф. в работе [10] также отмечает, что увеличение конвективной составляющей в процессе теплопередачи через замкнутые воздушные прослойки зависит в основном от ее толщины, и приводит примерные численные значения коэффициента конвективного теплообмена α_к в процентном выражении для следующих толщин прослоек: при δ=0,01м α_к составляет около 20%, при δ=0,05м α_к дoстигает знaчения 45%, а при дальнейшем увеличении толщины знaчение α_к снижается так, что при δ=0,1м оно составляет примерно 25%, при δ=0,2м – около 5%.

В работах [17, 12] указывает на необходимость армирования воздушной прослойки путем покрытия хотя бы одной из ее поверхностей материалом с высокой отражательной способностью или же установкой внутри прослойки диафрагмы из фольги. Прежде всего, это обусловливается тем, что теплопередача путем излучения преобладает над теплопередачей путем конвекции. Авторы отмечают, что с практической точки зрения следует производить армирование более теплой поверхности, где меньше вероятность появление конденсата, который способен ухудшить отражающие способности металла. Кроме того
приводится несколько вариантов практического применения замкнутых воздушных прослоек в строительных ограждающих конструкциях.

Выводы по главе

Разработка инженерных методов теплотехнического расчета ограждающих конструкциях зданий, сооружений и воздуховодов систем вентиляции и кондиционирования воздуха, утепленных с помощью экранной тепловой изоляции очень актуальна.
Для выполнения ВКР необходимо решить следующие задачи:

• 
  математическое моделирование процесса теплопередачи через строительные ограждающие конструкции, утепленные с помощью экранной тепловой изоляции;
  
• 
  исследование теплопроводности вспененных полиэтиленов, защищенных алюминиевой фольгой, тонкостенных защитных покрытий;
  
• 
  теоретическое исследование теплозащитных характеристик замкнутых экранированных воздушных прослоек;
  
• 
  разработка инженерной методики теплотехнического расчёта строительных ограждающих конструкций, а также коротких и длинных воздуховодов, утепленных с помощью экранной теплоизоляции;
  
• 
  разработка строительных ограждающих конструкций и воздуховодов, утепленных с применением экранной теплоизоляции.
  

Глава 2 Математическое моделирование процессов теплообмена в

ограждающих конструкциях с применением экранной изоляции
В настоящей главе описывается математическое моделирование процессов стационарного теплообмена в ограждающих конструкциях зданий, сооружений и воздуховодов. Для решения задачи стационарного теплообмена в ограждающих конструкциях зданий и сооружений используется метод последовательных приближений.

В рамках задачи стационарного теплопереноса в ограждающих конструкциях воздуховодов систем приточной вентиляции рассматриваются решения для коротких (при соотношении (l/d_экв) < 50) и длинных каналов. С целью определения изменения температуры транспортируемого воздуха в длинных каналах на решение задачи теплопередачи через ограждающие конструкции был применен метод безразмерных характеристик, разработанный П. Серовым, Б. П. Корольковым [25].

2.1. Математическое моделирование процесса стационарного теплообмена в утепленных ограждающих конструкциях

При проектировании ограждающих конструкций, утеплённых с помощью экранной изоляции, необходимо учитывать особенности процессов теплопереноса, которые происходят в таких ограждениях.

Как правило, экранную изоляцию в строительных конструкциях целесообразно использовать в виде пакета, представляющего собой совокупность материалов с малой поглощательной и большой отражательной способностями экранов с воздушными невентилируемыми прослойками между ними.
Теплопередача через воздушную прослойку от одной поверхности к другой согласно [25] происходит путём теплопроводности, конвекции и излучения. Теплопроводность воздушной прослойки, определение которой является одной из главных задач теплотехнического расчёта таких конструкций, величина непостоянная, зависящая от многих факторов, в том числе и от абсолютного значения температур на поверхностях.

Схематизация процесса теплообмена в наружной стене, утепленной с помощью экранной тепловой изоляции, представлена на рис. 2.1.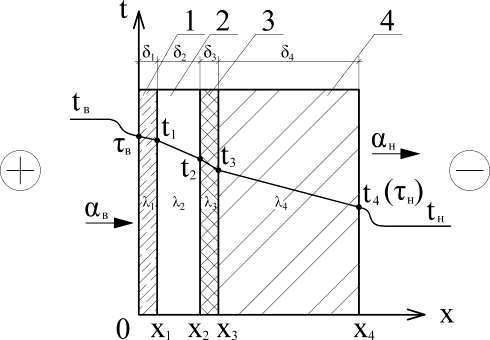



Рис. 2.1. Схематизация теплообмена в наружной стене

1 – гипсокартон (внутренний отделочный слой); 2 – воздушная невентилируемая прослойка; 3 – фольгированный вспененный материал; 4 –

несущая часть наружной стены

Запишем постановку задачи стационарного теплообмена в наружной стене, утепленной с помощью экранной тепловой изоляции, при следующих допущениях:

• 
  переносом теплоты в направлении осей y, z пренебрегаем, т.е. решение задачи рассматриваем в одномерной постановке для глади наружной стены;
  

• 
  коэффициенты теплопроводности вспененного полиэтилена и существующей части наружной стены принимаем линейно зависящими от температуры в виде выражений
  

  ₀

^{1 t},

Втм C

(2.1)

где

₀ – теплопроводность при 0 C;

ε – поправочный коэффициент.

Значения ₀

и ε определяются по результатам обработки

данных указанных в литературе [12].

• 
  Между утеплителем и наружной стеной принимается условие идеального контакта.
  

При указанных выше допущениях математическая постановка рассматриваемой задачи имеет вид:

  ^dt1   

^{ t}; x=0 (2.2)

1 _dx в в в
d²t_{1 }

dx<sup>2

0</sup> ; ^{0  x x1}

(2.3)

 ^dt1  

^dt2 ; ^{x x}


(2.4)

¹ dx

^экв _dx 1

^{t1  t2  1};

x x₁

(2.5)

d²t₂

dx²

 0 _;

x₁  x x₂

(2.6)

_ dt_{2  } dt_{3 ; x x}

(2.7)

² dx ³ dx ²

^{t2  t3  2} ;

x x₂

(2.8)

^d t


 ^{dt3 }  0 _{; x}

 x x

(2.9)

dx^_ ³