ВКР ДРАНИЧКИНА ЕЛЕНА. Экранной изоляции

• Название: Экранной изоляции
• Анкор: ВКР ДРАНИЧКИНА ЕЛЕНА
• Дата: 09.11.2022
• Размер: 0.79 Mb.
• Имя файла: VKR_Dranichkina_11324095.docx
• Тип: Обзор; #778873
• страница: 7 из 16



R_i _ⁱ

, (2.37)

i

δ_i– толщина i-го слоя конструкции, м

λ_i– теплопроводность i-го слоя конструкции,

Вт/м С.

Вычислив значение удельного теплового потока q, последовательно определяются температуры на внутренней и наружной поверхностях и на стыках слоев τ_в, τ₁, τ₂, τ₃, τ₄, τ_н.

Температуры на стыках слоев определяется по формуле

  t

_ ^{tв tн}₍1 _{ }

18. 
    , ^C
    

(2.38)

R


i в i1

о в

где

^ _i– температура на поверхности i-го слоя,

• 
  ^C;
  

^ i1 ^R
– сумма термических сопротивлений i-1 слоёв конструкции до

^{рассматриваемого сечения,} м² С/Вт^.

Далее определяются среднеинтегральные значения коэффициентов теплопроводности теплоизоляционного и стенового материалов рассматриваемой конструкции и эквивалентный коэффициент теплопроводности воздушной прослойки λ_экв. Уточняется значение сопротивления теплопередаче R₀ и величина удельного теплового потока q. Расчет повторяется до достижения необходимой точности.

Данная методика позволяет учесть влияние направления теплового потока, отражательные способности поверхностей материалов и значения температур ограничивающих поверхностей на термическое сопротивление воздушной прослойки.

В качестве примера рассмотрим теплотехнический расчёт конструкции, представленной на рис. 2.2.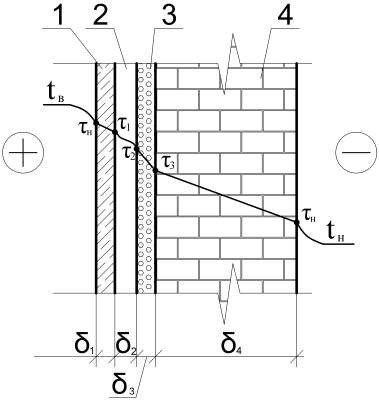


Рис. 2.2. Конструкция с экранной изоляцией

1. 
   – гипсокартонный лист:
   

^{1  0,02}м,

₁  0,34 Вт/^м С^;

2. 
   – воздушная прослойка:
   

₂  0,015м;

3 – пенофол: ^₃ ^{ 0,01} м,

₃  0,033 Вт/^м С^;

4 – кладка из силикатного кирпича:

₄  0,02м,

₄  0,76 Вт/^м С^.

Примем, что температура наружного воздуха t_н составляет –30

• 
  ^C, а
  

температура внутреннего воздуха t_в=20

• 
  ^C.
  

1. 
   В первом приближении по [24] примем значения термических сопротивлений для экранированных воздушных прослоек R₂и R₄равными 0,28
   

^{и 0,3} м² С/Вт^.

2. 
   Определим сопротивление теплопередаче ограждающей конструкции по формуле (2.36)
   

R_о

1


8,7

_ 0,02

0,34

 0,28 

0,01 _

0,033

0,51 _

0,76

¹ 1,47 ^,

23

м²  СВт

3. 
   По формуле (2.38) определим температуре на стыке слоев:
   

  20  ^2030 ¹  16,09C<sup>;

в</sup>1,47 8,7

  20  ^2030  ^1  ^{0,02 }  14,09C^;





¹ 1,47 ^ 8,7 0,34 ^


_{  20 } ^2030 _ ¹

 ^0,02  0,28^  4,57C;

² 1,47 ^ 8,7

0,34 ^


^{  20  2030 1  0,02  0,28 0,01   5,74C};




³ 1,47

^ 8,7

0,34

0,033^

_{  20 } 2030 _1 _ 0,02 _{ 0,28 }0,01

^{ 0,51  28,57C}.


^н1,47

^ 8,7

0,34

0,033

0,76 ^

4. 
   
   
   Определяем значение эквивалентного коэффициента теплопроводности воздушной прослойки по формуле (2.32), предварительно определив значения всех величин, входящих в эту формулу:
   

  0,024 Вт/^мС^;

₁  1,36 10^5 м² /с;

^{Pr  0,71};

^{ } 1 ^

_0.3

^ g^3 _{ }

^₁  ₂  ^

  ^

_ 0,5 ₁  ₂

 273_{ }

v
_к0,105_{ 2}





Pr_ 





^  
^{ 1} 14,09  4,57

0,5 14,09  4,57  273

_0,3



 0,105^







1,36 10^5

0,71^







 1,29 ^;

^_14,09  273_⁴ _ 4,57  273_^{4 }

5,67_

100

 ^ 

100 ^{ }

 ^{}  0,202^{Вт ;}

^л ¹ _¹ _ _{  }

м²  С


^ 0,8

0,04

1_ 14,09



4,57

^экв
 0,024 1,29  0,202  0,015  0,034

Вт_;

м С

5. С учетом

^'экв

рассчитываем сопротивление теплопередаче ограждающей

конструкции по формуле (2.36)

R_о

1


8,7

_ 0,02 _

0,34

0,015 _

0,034

0,01 _

0,033

0,51 _

0,76

¹  1,63^,

23

м²  СВт

Полученное сопротивление теплопередаче ограждающей конструкции отличается от первоначального его значения, поэтому необходимо производить

расчет с п.2 по п.5 до тех пор, пока вновь полученные величины

^экв ^не

достигнут заданной точности и не перестанут отличаться от значений, полученных в предшествующем приближении. В данном примере было использовано дополнительно два подобных приближения, в результате чего получено окончательное значение коэффициента теплопроводности воздушной прослойки в рассматриваемой конструкции:

^экв

 0,037

Вт_.

м С

На рис. 2.3 представлена зависимость термического сопротивления воздушной прослойки от ее толщины, полученная в результате расчета по изложенной выше методике, и зависимость термического сопротивления воздушной прослойки от ее толщины, полученная по данным [104].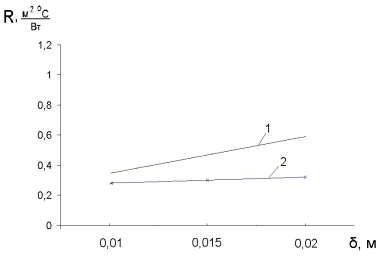


Рис. 2.3. Зависимость термического сопротивления воздушной прослойки

от её толщины

1 – расчётные данные автора; 2 – данные [24]
В целях упрощения подбора толщины воздушной прослойки для ограждающих конструкций наружных стен предлагается использовать номограмму, представленную на рис. 2.4, позволяющую определить требуемую толщину прослойки при расположении её с внутренней поверхности ограждения.

Для того, чтобы воспользоваться номограммой, в качестве исходных

данных необходимо принять термическое сопротивление неутепленной

^{ограждающей конструкции Rст,} м² С/Вт^{, значение коэффициента}

теплотехнической однородности r, и следовать описанному ниже алгоритму подбора толщины воздушной прослойки.

1. 
   Согласно [24] определить нормируемое значение сопротивление
   

0
теплопередаче ограждающей конструкции

^Rнорм, м² С/Вт^.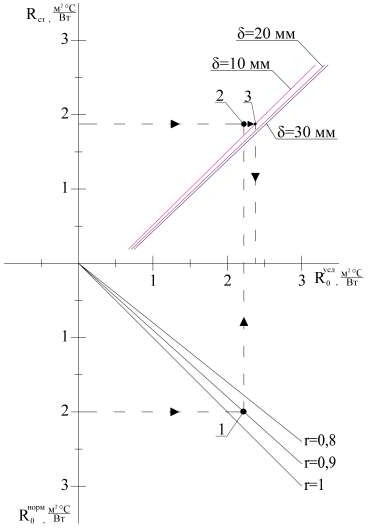

Рис. 2.4. Номограмма для определения толщины воздушной прослойки

2. 
   По значению
   

норм


R
0

и величине rграфическим путем определяем

величину абсциссы точки пересечения (точка 1). На оси ординат откладываем

значение термического сопротивление неутепленной стены R_сти проводим горизонтальную линию до пересечения с вертикальной линией, проведенной вверх из точки 1.

3. 
   Из точки 2 проводим горизонтальную линию до пересечения наклонной прямой, характеризующую зависимость между термическим
   

сопротивлением неутепленной стены и сопротивлением теплопередаче

усл


R
0

глади, утепленной наружной стены при определении толщины воздушной прослойки.

2. 
   Математическое моделирование процесса теплопередачи в ограждающих конструкциях утепленных воздуховодов
   

При проектировании систем вентиляции с целью поддержания постоянства температуры приточного воздуха возникает необходимость в теплоизоляции воздуховодов, что следует из анализа работ [11, 12, 22]. В системах кондиционирования воздуха, особенно в теплый период года, необходимо уменьшить нагрев приточного воздуха.

Оценить эффективность применения экранной теплоизоляции при утеплении воздуховодов систем вентиляции и кондиционирования возможно на основании данных теплотехнического расчета конструкций воздуховодов с применением указанных выше материалов. Следует отметить, что в ходе расчета необходимо определить не только теплозащитные характеристики рассматриваемых конструкций, но и найти величину изменения температуры транспортируемого воздуха на изолируемом участке воздуховода.

Решить поставленную задачу можно, рассмотрев процесс взаимосвязанного теплообмена между изолированным трубопроводом и движущимся в нем воздухом, который описывается системой дифференциальных уравнений теплопроводности в трубопроводе и уравнении энергии для движущегося потока воздуха, решение которой приведено в [25,

26]. С физической точки зрения рассматриваемый воздуховод можно считать рекуперативным теплообменным аппаратом с постоянной температурой окружающего воздуха.

1. 
   Математическое моделирование процесса стационарного теплообмена в ограждающих конструкциях коротких воздуховодов
   

Используемые в настоящее время воздуховоды, имеющие отношение

l/ d_экв  50, относятся к коротким каналам, в которых существенное влияние оказывает начальный участок на значение коэффициента теплоотдачи. В

коротких каналах значение местных коэффициентов теплоотдачи значительно выше по сравнению со значениями тех же коэффициентов для стабилизированного теплообмена [27]. В связи с этим возникает необходимость в разработке инженерной методики, учитывающей влияние переменности теплоотдачи на теплопотери изолированного воздуховода.

Схематизация процесса стационарного теплообмена в изолированном воздуховоде с помощью экранной тепловой изоляции представлена на рис. 2.5.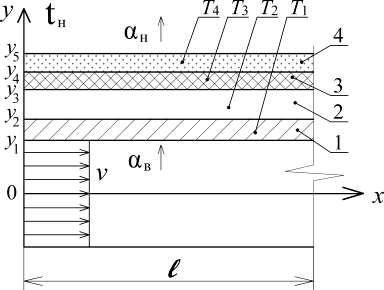



Рис. 2.5. Схематизация процесса стационарного теплообмена в изолированном воздуховоде с помощью экранной тепловой изоляции

1 – стенка воздуховода; 2 – воздушная прослойка; 3 – фольгированный вспененный полиэтилен; 4 – защитный короб
Решение рассматриваемой задачи стационарного теплообмена выполним при следующих допущениях:

• 
  передачей теплоты путем теплопроводности в направлении осей x и z пренебрегаем;
  
• 
  режим течения воздуха в воздуховоде считаем турбулентным.
  

При указанных выше допущениях математическая постановка задачи примет следующий вид:

r^d  

  T  0 _{; y=y ;}
0  x l
(2.22)

dx
d²T₁

dy²

1

 0 _;

1


^{y1  y y2} ;

1


0  x l


(2.23)

 ₁

dT₁ dy