Эквивалентные структурные преобразования. Эквивалентные структурные преобразования
 Скачать 49.57 Kb.
|
|
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИ РОССИЙСКОЙ ФЕДЕРАЦИИ федеральное государственное бюджетное образовательное учреждение высшего образования «ТЮМЕНСКИЙ ИНДУСТРИАЛЬНЫЙ УНИВЕРСИТЕТ» МНОГОПРОФИЛЬНЫЙ КОЛЛЕДЖ ОТДЕЛЕНИЕ АВТОМАТИЗАЦИИ И ЭЛЕКТРОТЕХНИЧЕСКИХ СИСТЕМ Реферат на тему: Эквивалентные структурные преобразования Выполнили: студенты группы АТПт-18-(9)-1 Кузнецов Данил Олегович проверил: Ширшова Н.О. ____________ Тюмень 2021 ВВЕДЕНИЕ Структурная схема — это совокупность элементарных звеньев объекта и связей между ними, один из видов графической модели. Под элементарным звеном подразумевается часть объекта, системы управления и т. д., которая реализует элементарную функцию. САУ представляет собой систему, состоящую из функциональных элементов, каждый из которых может быть представлен в виде динамического звена. То есть САУ можно представить в виде совокупности динамических звеньев с известными математическими моделями. 1 Эквивалентные структурные преобразования Рассмотрим структуру типичной САУ на рисунке 1.1. 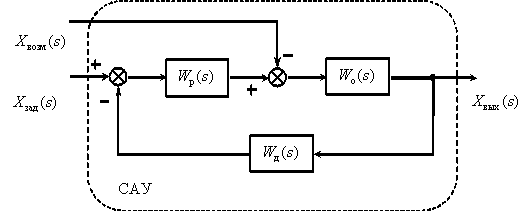 Рисунок 1.1 - Структура типичной САУ. 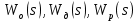 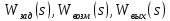- передаточные функции соответственно объекта, датчика и регулятора,  - изображения задающего, возмущающего и выходного сигналов.В процессе анализа и синтеза САУ необходимо получать передаточные функции САУ, которые связывают выходную переменную с заданием и возмущением в САУ, по известным структурной схеме и передаточным функциям динамических звеньев, входящих в состав САУ. Аналогичная задача возникает в том случае, когда известны частотные характеристики динамических звеньев, а необходимо определить частотные характеристики САУ, характеризующие связи между выходом и входом САУ. Решением этих задач мы и займемся в дальнейшем. Эта задача решается путем преобразования (сворачивания) структурной схемы к одному динамическому звену с искомой передаточной функцией на основе использования правил эквивалентных преобразований структурных схем и принципа суперпозиции (наложения). Правила эквивалентных преобразований позволяют найти необходимую передаточную функцию САУ, свернув структурную схему к одному динамическому звену с искомой передаточной функцией. Рассмотрим правила эквивалентных преобразований, не изменяющих свойств систем и необходимых для нахождения передаточной функции: Рассмотрим правила эквивалентных преобразований, не изменяющих свойств систем и необходимых для нахождения передаточной функции: Последовательное соединение динамических звеньев (рисунок 1.2).  Рисунок 1.2 - Последовательное соединение динамических звеньев. Параллельное соединение динамических звеньев (рисунок 1.3). 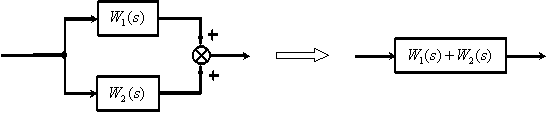 Рисунок 1.3 - Параллельное соединение динамических звеньев. Замкнутый контур с отрицательной обратной связью (рисунок 1.4). 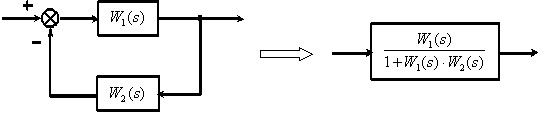 Рисунок 1.4 - Замкнутый контур с отрицательной обратной связью. Замкнутый контур с положительной обратной связью (рисунок 1.5). 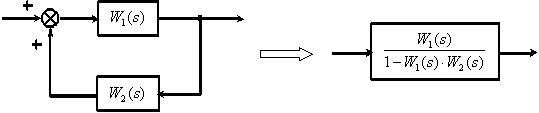 Рисунок 1.5 - Замкнутый контур с положительной обратной связью. Перенос точки ветвления через динамическое звено (рисунок 1.6). 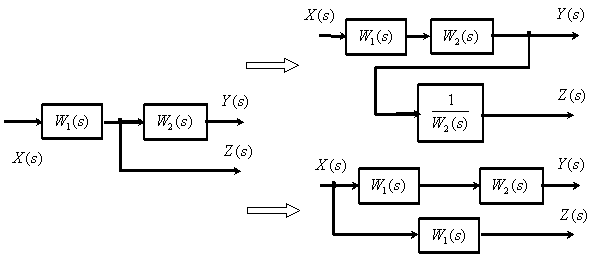 Рисунок 1.6 - Перенос точки ветвления через динамическое звено. Перенос суммирующего звена через динамическое звено (рисунок 1.7). 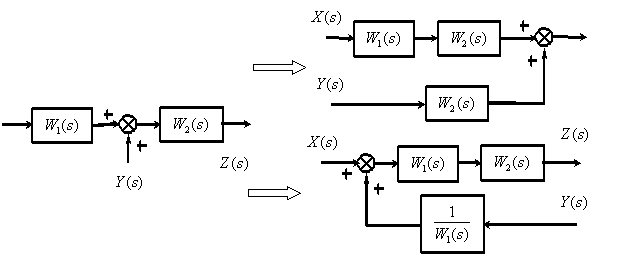 Рисунок 1.7 - Перенос суммирующего звена через динамическое звено. Перестановка суммирующих звеньев (рисунок 1.8). 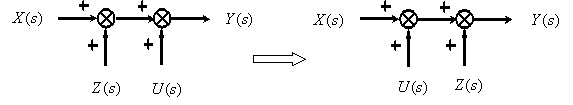 Рисунок 1.8 - Перестановка суммирующих звеньев. Перенос точки ветвления с выхода на вход суммирующего звена (рисунок 1.9). 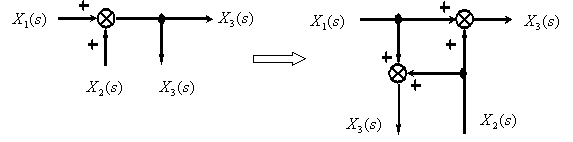 Рисунок 1.9 - Перенос точки ветвления с выхода на вход суммирующего звена. Перенос точки ветвления с входа на выход суммирующего звена (рисунок 1.10). 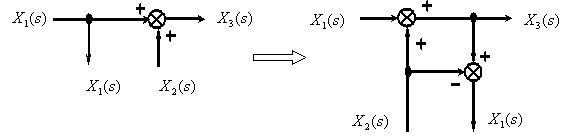 Рисунок 1.10 - Перенос точки ветвления с входа на выход суммирующего звена. |