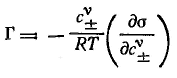колды_ответы. Экзаменационный билет 1
 Скачать 3.42 Mb.
|
 Экзаменационный билет № 2
Есть несколько определений поверхностного натяжения:
Термодинамическое определение поверхностного натяжения вытекает из объединенного уравнения первого и второго начал термодинамики. Запишем его для гетерогенной системы относительно изменения внутренней энергии U:  При постоянных S, V, ni и q имеем:  т. е. поверхностное натяжение есть частная производная от внутренней энергии по площади поверхности раздела фаз при постоянных энтропии, объеме, числе молей компонентов и заряде. Так как объединенное уравнение первого и второго начал термодинамики может быть записано и относительно других термодинамических потенциалов, а именно энергии Гиббса G, энергии Гельмгольца F и энтальпии Я, то при соответствующих постоянных параметрах получим:  Таким образом, поверхностное натяжение есть частная производная от любого термодинамического потенциала по площади межфазной поверхности при постоянных соответствующих параметрах. Физический смысл поверхностного натяжения можно представить так: поверхностное натяжение на границе жидкости с газовой фазой – работа, расходуемая на обратимый разрыв столбика этой жидкости с поперечным сечением в 0,5 единицы площади, так как при разрыве образуется новая поверхность, равная единице площади. Чем сильнее межмолекулярные связи в данном теле, тем больше его поверхностное натяжение на границе с газовой фазой. В соответствии со вторым началом термодинамики избыточная энтропия равна  Учитывая, что Gs = σ, получим следующее выражение:  Из этого уравнения следует, что внутренняя энергия поверхности складывается из энергии Гиббса и теплоты образования поверхности. Для индивидуальных веществ теплота qs всегда положительна, так как при образовании поверхности теплота поглощается. Из уравнения объединенных первого и второго начала термодинамики при постоянстве всех параметров, кроме температуры, имеем:  Подставлям это выражение в полученные уравнения:  Это уравнение называется уравнением Гиббса — Гельмгольца. Оно связывает полную поверхностную энергию с энергией Гиббса (поверхностным натяжением). Из этого уравнения следует, что для определения полной поверхностной энергии необходимо знать зависимость поверхностного натяжения от температуры. Для индивидуальных веществ теплота qs всегда положительна, а это значит, что температурный коэффициент поверхностного натяжения отрицателен:  Таким образом, поверхностное натяжение индивидуальных веществ на границе с газом (воздухом) снижается с повышением температуры. Для большинства неполярных жидкостей эта зависимость линейная.
Различают три возможных механизма образования двойного электрического слоя:
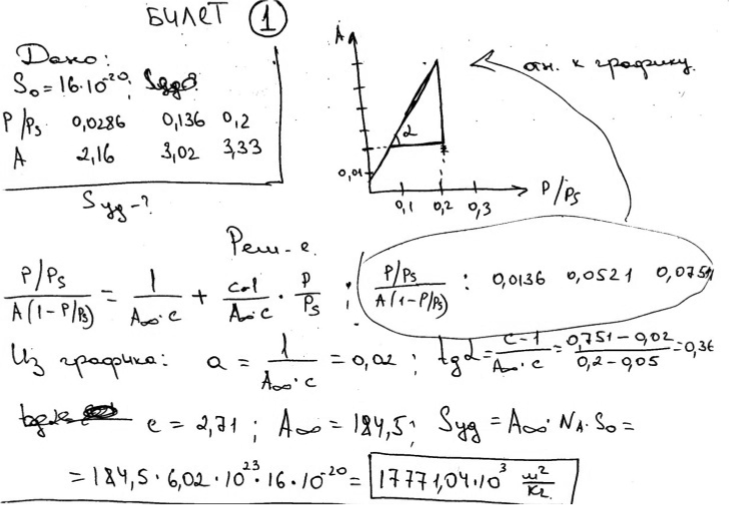
Из объединенных первого и второго начал термодинамики, а также полного дифференциала энергии Гиббса выводится первое уравнение Липпмана, связывающее электрический потенциал с поверхностным натяжением:  Если знаки потенциала и заряда совпадают, то поверхностное натяжение снижается с ростом потенциала. Если же их знаки противоположны, то увеличение потенциала ведет к росту поверхностного натяжения. Эти зависимости тем сильнее,чем больше абсолютное значение плотности заряда. При минимальной плотности заряда поверхностное натяжение слабо зависит от потенциала. Дифференциальная емкость двойного электрического слоя, как н любого конденсатора, определяется соотношением:  После дифференцирования первого уравнения Липмана по φ и подстановки в него данного соотношения получим второе уравнение Липпмана:  Это уравнение показывает возможность определения емкости двойного электрического слоя, если известна зависимость σ от φ.  Это уравнение называют уравнением электрокапиллярной кривой. Из него следует, что поверхностное натяжение при условии постоянства емкости двойного электрического слоя изменяется в соответствии с уравнением параболы. 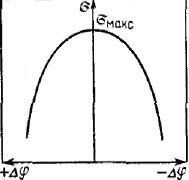 Вершина параболы отвечает максимальному поверхностному натяжению σмакс. Парабола симметрична, что по физическому смыслу означает равное сродство катионов и анионов, выступающих в роли противоионов, к поверхности, имеющей соответственно отрицательный и положительный потенциал. Уменьшение положительного потенциала, как и отрицательного, ведет к увеличению поверхностного натяжения. Однако в реальных системах емкость двойного электрического слоя несколько изменяется с изменением потенциала, и поэтому экспериментальные электрокапиллярные кривые обычно не являются симметричными. Вершина параболы соответствует точке нулевого заряда. В этой точке поверхностное натяжение не зависит от потенциала, так как производная dσ/dφ равна нулю, т. е. поверхностный слой имеет нулевой заряд, что означает отсутствие двойного электрического слоя. Потенциал же поверхности в этой, точке не равен нулю.
 Экзаменационный билет № 3
Для описания термодинамики поверхностных явлений применяют два метода: метод избыточных величин Гиббса и метод «слоя конечной толщины». Ч 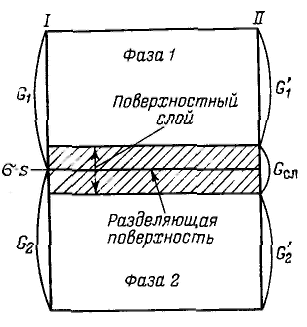 тобы не определять границы поверхностного слоя (поверхности разрыва по Гиббсу), Гиббс предложил относить все изменения термодинамических параметров в слое в сравнении с параметрами объемной фазы к разделяющей поверхности, не имеющей объема или толщины (метод избыточных величин Гиббса). При таком рассмотрении поверхность характеризуется избыточными термодинамическими параметрами, непосредственно отражающими проявление поверхностной энергии. Объемные фазы считаются однородными вплоть до разделяющей поверхности. В соответствии с методом избыточных величин энергия Гиббса системы равна сумме энергий Гиббса G1 и G2 объемных фаз 1, 2 и поверхностной энергии Гиббса σs, которая является избыточной: Характеристика величины адсорбции определяющася избытком вещества в поверхностном слое определенной толщины по сравнению с его количеством в таком же объеме фазы, также отнесенным к единице площади поверхности или единице массы адсорбента, называется гиббсовской адсорбцией и обозначается буквой гамма Г (метод избыточных величин Гиббса). Объединенное уравнение первого и второго начал термодинамики для внутренней энергии поверхности с учетом поверхностной и химической энергии имеет вид (объем поверхностного слоя равен нулю)   Так как внутренняя энергия поверхности пропорциональна экстенсивным величинам, то и ее полный дифференциал от тех же переменных запишется следующим образом:   Подставляя значение dU, получим: Д  ля условия постоянства температуры это соотношение принимает вид Разделив полученное уравнение на площадь поверхности, получим: Данное уравнение называют фундаментальным адсорбционным уравнением Гиббса. Для адсорбции одного конкретного вещества при постоянных химических потенциалах других веществ полученное уравнение можно записать относительно частной производной для данного компонента:  Принимая во внимание, что  Для гиббсовской адсорбции это выражение принимает вид 
|
