колды_ответы. Экзаменационный билет 1
 Скачать 3.42 Mb.
|
Гидрозоль AgI получен добавлением 8 мл КI с концентрацией 0,05 моль/л к 10 мл раствора AgNO3 с концентрацией 0,02 моль/л. Напишите формулу мицеллы образовавшегося золя и объясните строение ДЭС.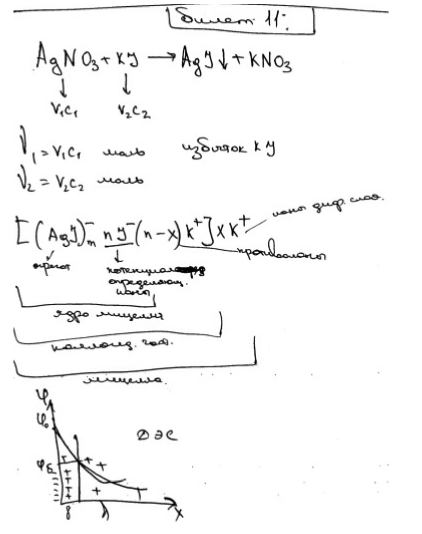 Экзаменационный билет № 12
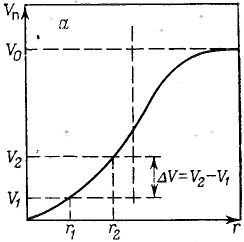
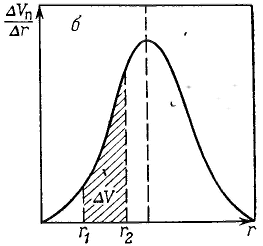
Удерживание газов и паров пористыми телами, т. е. их адсорбционная способность, зависят как от природы взаимодействующих тел, так и от структуры пористого тела. Если структурный фактор для макропористых адсорбентов имеет малое значение, то уже для переходнопористых тел его роль резко возрастает. Это обусловлено в первую очередь проявлением капиллярных сил. Чем меньше размер пор, тем сильнее капиллярное удерживание адсорбата. В противном случае (если поверхность не смачивается) наблюдается капиллярное выталкивание вещества из пор, адсорбция на несмачиваемых телах минимальна и возможна только на ровной поверхности и в крупных порах. Адсорбция на переходнопористых телах происходит в основном по механизму капиллярной конденсации. Капиллярная конденсация начинает проявляться при определенной степени заполнения адсорбента или при определенном значении давления пара, характерном для данной системы. Д 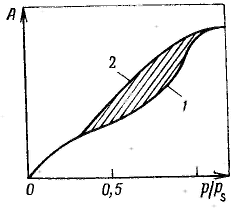 ля адсорбентов с переходными порами характерна изотерма адсорбции с петлей капиллярно-конденсационного гистерезиса. Адсорбции соответствует нижняя кривая, а десорбции — верхняя. При малых давлениях, когда не происходит капиллярная конденсация, гистерезиса не наблюдается. Начало появления гистерезиса зависит от природы адсорбента и адсорбата.К 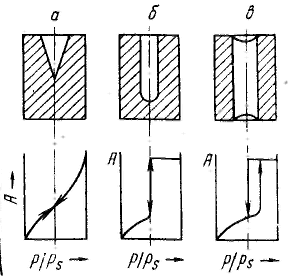 онденсация на стенках цилиндрической поры приводит к уменьшению диаметра поры, что вызывает ее мгновенное заполнение при давлении, отвечающем началу конденсации. На концах поры образуются сферические мениски жидкости. Десорбция может начаться только при давлении, соответствующем радиусам кривизны этих менисков. Таким образом, опорожнение капилляра происходит при меньшем давлении, чем его заполнение. Этим объясняется появление петли капиллярно-конденсационного гистерезиса.Капиллярная конденсация описывается уравнением Кельвина, в которое входит радиус кривизны мениска, и это позволяет использовать его для расчета функции распределения пор по размерам. Метод расчета функций распределения частиц (пор) по размерам заключается в построении интегральных и дифференциальных кривых распределения. Для пористых тел принято характеризовать распределение пор по их радиусам, поэтому интегральная кривая распределения выражает зависимость общего объема пор от их радиуса:  .Другой функцией распределения для данного пористого тела является зависимость f(rп) или dVп/drп от rп, которая называется дифференциальной кривой распределения. Она более четко и наглядно характеризует полидисперсность системы.
Для получения кривых распределения по методу капиллярной конденсации используют десорбционную ветвь изотермы адсорбции, так как для всех без исключения пор она соответствует сферическим менискам, радиусы которых принимают за радиусы пор.
Рассмотрим зависимость от расстояния энергии притяжения частиц — молекулярной составляющей расклинивающего давления. Из сил Ван-дер-Ваальса наиболее универсальны и существенны лондоновские силы дисперсионного взаимодействия. Энергия электростатического отталкивания пластин равна  .Для вывода уравнения энергии молекулярного притяжении между частицами воспользуемся уравнением энергии притяжения одной молекулы (атома) к поверхности адсорбента (в данном случае частицы):  Приращение энергии молекулярного притяжения, отнесенное к единице площади, пропорционально приращению числа молекул (атомов) в цилиндре с основанием, равным единице площади, т. е. ndr:  После интегрирования получим:  Величина A12 в уравнении называется константой Гамакера. Она учитывает природу взаимодействующих тел. Эта константа выражается в единицах энергии и имеет значение порядка 10-19 Дж. Чем сильнее взаимодействует дисперсная фаза со средой, тем меньше константа Гамакера, это значит, что силы притяжения между частицами уменьшаются. Для области малых потенциалов суммарная энергия взаимодействия равна 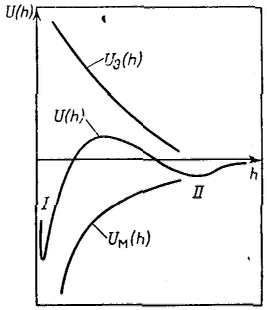  Первичный минимум I отвечает непосредственному слипанию частиц, а вторичный минимум II — их притяжению через прослойку среды. Максимум, соответствующий средним расстояниям, характеризует потенциальный барьер, препятствующий слипанию частиц. Потенциальный барьер увеличивается с уменьшением константы Гамакера.
 Экзаменационный билет № 13
Потенциальная теория Поляни была предложена для термодинамического описания полимолекулярной адсорбции. Она устанавливает связь величины адсорбции с изменением давления пара (газа) и с теплотами адсорбции, исходя из объема адсорбционного пространства. Наиболее удачно теория Поляни предсказывает зависимость величины адсорбции от температуры. Модель адсорбции в теории Поляни предполагает, что адсорбат ведет себя термодинамически как однокомпонентная система, находящаяся в потенциальном поле поверхностных сил адсорбента, который химически инертен. Теория Поляни принимает, что в адсорбционном пространстве действуют только дисперсионные силы, которые, во-первых, аддитивны, во-вторых, не зависят от температуры. Введено допущение, что практически все адсорбированное вещество находится на поверхности в жидком состоянии. Это допущение в большой мере соответствует состоянию адсорбата в порах пористых адсорбентов. Именно поэтому подход, используемый в теории Поляни, оказался более пригодным для описания адсорбции на пористых адсорбентах, в порах которых происходит конденсация паров. За меру интенсивности адсорбционного взаимодействия принят адсорбционный потенциал — работа переноса 1 моль пара, находящегося в равновесии с жидким адсорбатом в отсутствие адсорбента (давление ps) в равновесную с адсорбентом паровую фазу (давление р):  .Этот потенциал характеризует работу против действия адсорбционных сил. Каждой точке изотермы адсорбции соответствуют определенные значения А и p/ps, которые позволяют получить значения V и ε, т. е. найти зависимости адсорбционного потенциала от объема адсорбата на адсорбенте — потенциальную кривую адсорбции. Т 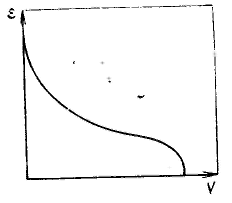 ак как дисперсионные силы не зависят от температуры, то от температуры не должна зависеть и форма потенциальной кривой адсорбции, что экспериментально подтверждается во многих случаях. Экспериментальные точки при разных температурах ложатся на одну и ту же кривую ε = f(V), которую поэтому называют характеристической кривой: , т. е. адсорбционный потенциал при постоянном объеме жидкого адсорбата на адсорбенте (постоянной степени объемного заполнения) не зависит от температуры (температурная инвариантность характеристической кривой).Важная особенность потенциальных кривых адсорбции, заключается в том, что характеристические кривые для одного и того же адсорбента и разных адсорбатов при всех значениях объемов адсорбата в поверхностном слое находятся в постоянном соотношении β:  Коэффициент β был назван коэффициентом аффинности, Отсюда следует, что, зная характеристическую кривую для одного адсорбата и коэффициент аффинности для другого адсорбата по отношению к первому, можно вычислить изотерму адсорбции второго адсорбата на том же адсорбенте.
Широкое признание и распространение получила теория устойчивости и коагуляции, учитывающая электростатическую составляющую расклинивающего давления (отталкивание) и его молекулярную составляющую. (притяжение). Эта теория удовлетворительно описывает закономерности поведения типично лиофобных дисперсных систем, для которых можно пренебречь адсорбционно-сольватным фактором устойчивости. В наиболее общем виде эта теория была разработана советскими учеными Б. В. Дерягиным и Л. Д. Ландау в 1937 — 1941 гг. и несколько позднее независимо от них голландскими учеными Фервеем и Овербеком; по первым буквам фамилий этих ученых теория названа теорией ДЛФО. Она рассматривает процесс взаимодействия частиц по отдельным стадиям — перекрывание их поверхностных слоев и возникновение расклинивающего давления, используя при этом понятие потенциального барьера, аналогичное энергии активации в химической кинетике. Расклинивающее давление возникает при сильном уменьшении толщины пленки (прослойки) в результате перекрывания (взаимодействия) поверхностных слоев (поверхностей разрыва). С расклинивающим давлением связана целая область явлений, включающая устойчивость дисперсных систем и пленок, полимолекулярную адсорбцию, набухание, массоперенос в дисперсных системах и др. В гетерогенных системах под пленкой понимают тонкую часть системы, находящуюся между двумя межфззными поверхностями. При уменьшении толщины пленки ограничивающие ее поверхностные слои начинают перекрываться (h<2σ), вследствие чего возникает давление, обусловленное взаимодействием как сближающихся фаз, так и межфазных слоев — расклинивающее давление. Таким образом, избыточные термодинамические функции тонкой пленки зависят от, ее толщины h. 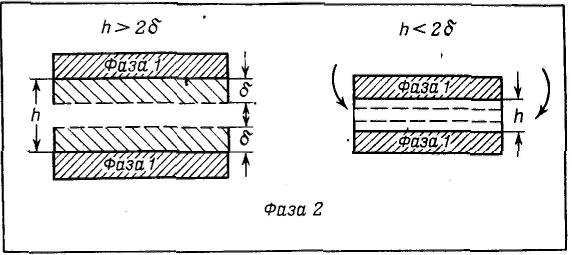 Таким образом, расклинивающее давление можно рассматривать как разность гидростатических давлений в пленке и в окружающей пленку фазе или как приращение энергии Гиббса на данном расстоянии между поверхностными межфазными слоями, пересчитанное на единицу толщины пленки и отнесенное к единице площади перекрывания поверхностных слоев. Расклинивающее давление — суммарный параметр, учитывающий как силы отталкивания, так и силы притяжения, действующие в пленке. Общая энергия взаимодействия между двумя пластинами, приходящаяся на единицу их площади, равна  В теории ДЛФО (в ее классическом виде) принято, что давление отталкивания обусловлено только электростатическими силами, поэтому  .Давление Пэ обусловлено обычно стремлением системы к уменьшению поверхностной энергии, его природа связана с ван-дер-ваальсовыми силами. Для определения электростатической составляющей расклинивающего давления необходимо произвести интегрирование данного уравнения и ряд вычислений, который приведет к значению Пэ:  ,а затем и к  .Р 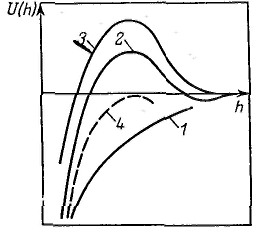 азличают три наиболее характерных вида потенциальных кривых, отвечающих определенным состояниям агрегативной устойчивости дисперсных систем. Кривая 1 соответствует такому состоянию дисперсной системы, при котором на любом расстоянии между частицами энергия притяжения преобладает над энергией отталкивания.Кривая 2 указывает на наличие достаточно высокого потенциального барьера и вторичного минимума. В системе, находящейся в таком состоянии, происходит быстрая флокуляция частиц (перед вторичным минимумом отсутствует потенциальный барьер) на расстояниях, соответствующих вторичному минимуму. Кривая 3 отвечает состоянию системы с высоким потенциальным барьером при отсутствии вторичного минимума или при его глубине, меньшей тепловой энергии (kбT). Вероятность образования агрегатов частиц в таких условиях очень мала, и дисперсные системы обладают большой агрегативной устойчивостью.
 Экзаменационный билет № 14
На первый взгляд может показаться, что закономерности заполнения микропор должны следовать теории капиллярной конденсации. Однако размеры микропор таковы, что в них происходит перекрытие полей поверхностных сил противоположных стенок пор, что значительно повышает энергию адсорбции и искажает профиль мениска конденсата в порах, соответствующий уравнению Кельвина, т. е. приводит к дополнительному всасыванию адсорбата, резкому увеличению адсорбционного потенциала. Особенности адсорбции на микропористых телах проявляются в их избирательном действии. Избирательность, или селективность, микропористых адсорбентов существенно выше, чем переходнопористых, благодаря тому, что большинство адсорбированных молекул взаимодействуют непосредственно с поверхностью адсорбента. В более крупных порах такое взаимодействие характерно только для первого слоя. В последующих же слоях взаимодействие не зависит от природы·, адсорбента, а определяется только природой адсорбата. Кроме этой особенности у микропор может проявляться так называемый ситовой эффект, заключающийся в том, что адсорбироваться могут только те молекулы, размеры которых меньше размеров микропор или равны им, в связи с чем все микропористые адсорбенты (не только цеолиты) называют молекулярными ситами. Переходя к количественным соотношениям теории объемного заполнения пор, необходимо отметить, что в ее основе лежат представления потенциальной теории Поляни, предложенной первоначально для описания полимолекулярной адсорбции, исходя из двух основных параметров: адсорбционного потенциала ε, адсорбционного объема V и двух положений:  Степень заполнения адсорбента можно· представить как отношение величины адсорбции А к максимальной адсорбции А0, или как отношение заполненного объема V к предельному объему адсорбционного пространства V0, приведенных к нормальным условиям (давлению и температуре).  или  Эти уравнения являются общими уравнениями теории объемного заполнения микропор. Заменив адсорбционный потенциал на его выражение через давление пара (ε = RTln(p/ps)) и прологарифмировав общее уравнение теории объемного заполнения микропор, получим:  Для большинства активных углей n=2, тогда полученное уравнение переходит в уравнение Дубинина— Радушкевича:  Построение прямой в координатах  дает возможности найти константы этого уравнения A0 и E. Объем микропор Vп рассчитывают по уравнениям |
