колды_ответы. Экзаменационный билет 1
 Скачать 3.42 Mb.
|
|
Общее определение поверхностной активности дается соотношением:  которое справедливо как для неэлектролитов, так и для электролитов. Поверхностная активность, как и гиббсовская адсорбция, может быть положительной и отрицательной. Абсолютное значение и ее знак зависят от природы как адсорбируемого вещества, так и среды (растворителя). Если с увеличением концентрации вещества поверхностное натяжение на границе раздела фаз понижается, то такое вещество называют поверхностно-активным. Для таких веществ  Вещества, повышающие поверхностное натяжение на границе раздела фаз с увеличением концентрации, называют поверхностно-инактивными. Для них 
Ж 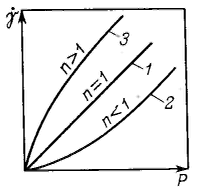 идкообразные тела классифицируют на ньютоновские и неньютоновские жидкости. Ньютоновскими жидкостями называют системы, вязкость которых не зависит от напряжения сдвига и является постоянной величиной в соответствии с законом Ньютона: P = η Течение неньютоновских жидкостей не следует закону Ньютона, их вязкость зависит от напряжения сдвига. В свою очередь, они подразделяются на стационарные, реологические свойства которых не изменяются со временем, и нестационарные, для которых эти характеристики зависят от времени. Среди неньютоновских стационарных жидкостей различают псевдопластические и дилатантные. Типичные зависимости скорости деформации жидкообразных тел от напряжения (кривые течения, или реологические кривые) представлены на рисунке.Общую зависимость напряжения сдвига от скорости деформации можно выразить в виде степенной функции:  Если n = 1, то данное соотношение переходит в уравнение Ньютона. Это двухпараметрическое уравнение известно под названием математической модели Оствальда — Вейля. Ньютоновская вязкость η неньютоновской стационарной жидкости определяется уравнением  .Если n = 1, жидкость является ньютоновской и константа k совпадает со значением ньютоновской вязкости (кривая 1). Таким образом, отклонение n от единицы характеризует степень отклонения свойств жидкости от ньютоновских. Основы теории вязкости разбавленных лиозолей (суспензий) были заложены Эйнштейном. Он исходил из гидродинамических уравнений для систем макроскопических твердых сферических частиц,, которые при сдвиге приобретают дополнительное вращательное движение. Возникающее при этом рассеяние энергии является причиной возрастания вязкости. Эйнштейном была установлена связь между вязкостью дисперсной системы η и объемной долей дисперсной фазы φ:  Формула Эйнштейна не учитывает наличия у частиц поверхностных слоев, таких как адсорбционные, сольватные и двойные электрические. Оно было получено в предположении отсутствия взаимодействия между частицами дисперсной фазы, поэтому оно справедливо только для разбавленных растворов. С увеличением концентрации дисперсной фазы взаимодействие частиц возрастает, и его необходимо учитывать. Одним из приборов для определения вязкости является капиллярный вискозиметр. При измерении капиллярным вискозиметром, вязкость рассчитывают по уравнению Пуазейля:  Для исследования вязкости неньютоновских жидкостей используется ротационный вискозиметр.
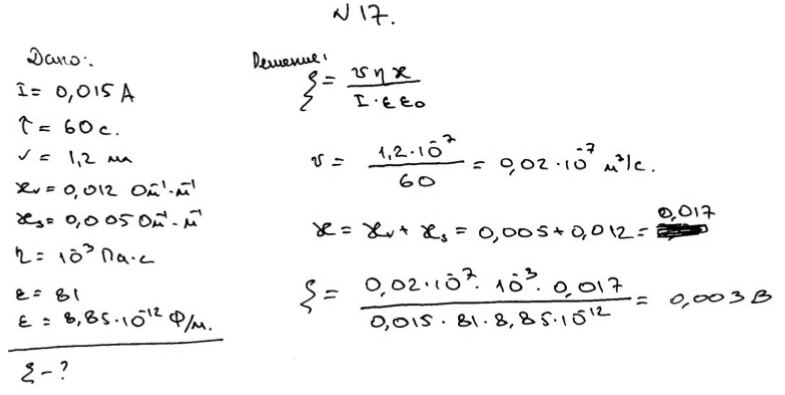 Экзаменационный билет № 18
Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие, или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы, называют адгезией (прилипанием). Смачивание— это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом). Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания). Капля жидкости, нанесенная на поверхность, может оставаться на ее определенном участке, и система будет находиться в равновесии в соответствии с законом Юнга, или же растекаться по поверхности. В обоих этих случаях система переходит в состояние с минимальной энергией Гиббса. Если капля не растекается, то, кал было показано выше, краевой угол зависит от соотношения работ адгезии Wа и когезии Wк смачивающей жидкости. Рассмотрим условия растекания жидкости 2 по поверхности 3. Изменение энергии Гиббса можно записать следующим пбразом:  Для самопроизвольного процесса dG<0 и ds>0:  Если разность заменить выражением из уравнения Дюпре, то получим или Разницу между левой и правой частями этих неравенств называют коэффициентом растекания f по Гаркинсу:  или При положительном значении коэффициента f жидкость растекается по поверхности, при отрицательном — нe растекается. Введение ПАВ уменьшает работу когезии (поверхностное натяжение) жидкости а значит, как следует из уравнения Дюпре-Юнга, увеличивает смачивание. Лучше смачивает та жидкость, которая имеет меньшее поверхностное натяжение или работу когезии.
Принцип седиментационного метода анализа дисперсности состоит в измерении скорости осаждения частиц, обычно в жидкой среде. По скорости осаждения с помощью соответствующих уравнений рассчитывают размеры частиц. Метод позволяет определить распределение частиц по размерам и соответственно подсчитать их удельную поверхность. П 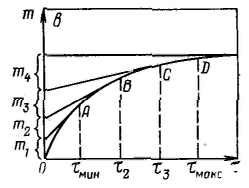 ри седиментационном анализе дисперсности полидисперсных систем определяют время осаждения частиц отдельных фракций, рассчитывают скорости их осаждения и соответствующие им размеры частиц. Для этого сначала измеряют зависимость массы осевшего осадка от времени, строят график этой зависимости, называемой кривой седиментации, по которому затем определяют все необходимые характеристики дисперсной системы.Имеются графические и аналитические методы расчета кривой седиментации. Реальная кривая седиментации полидисперсной системы обычно получается плавной и ей отвечает множество бесконечно малых участков, касательные в каждой точке этой кривой отражают седиментацию данной бесконечно малой фракции. Р 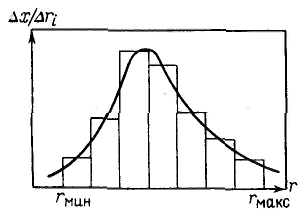 езультаты седиментациоиного анализа дисперсности полиднсперсных систем представляют также в виде кривых распределения частиц по размерам, характеризующих степень полидисперсности системы.Кривая распределения является наглядной и удобной характеристикой полидисперсности системы, по которой легко определить содержание различных фракций. Ее строят подобно кривой распределения пор по размерам. Обычно сначала получают интегральную кривую распределения, проводят ее выравнивание с учетом точности получаемых средних значений радиусов частиц фракций и затем по ней строят дифференциальную кривую распределения. Иногда дифференциальную кривую строят сразу. На оси абсцисс откладывают значения радиусов; на ось ординат наносят отношение приращения массовых долей к разности радиусов частиц соседних фракций Δx/Δri. Построив на графике отдельные прямоугольники для каждой фракции (гистограмму) и соединив плавной кривой середины их верхних сторон, получают дифференциальную кривую распределения частиц полидисперсной системы по размерам. Для осуществления седиментации ультрамикрогетерогенных систем русский ученый А. В. Думанский в 1912 г. предложил использовать центробежное поле. Этот способ удалось реализовать шведскому ученому Сведбергу, который разработал центрифугу с частотой вращения в несколько десятков тысяч оборотов в секунду. Центробежная сила Fц, как и нормальное ускорение а, пропорциональна кривизне траектории движения частицы (при постоянной линейной скорости u):  Равновесие между Fтр и Fц, которое наступает при седиментации, удобнее записать таким образом (чтобы оставить одну переменную от времени):  Разделяя переменные в полученном соотношении и интегрируя его в пределах от начального расстояния x0 до x и соответственно от τ = 0 до τ, получим:  или  По характеристикам седиментации в центробежном поле при частоте вращения ротора в несколько десятков тысяч оборотов в секунду можно рассчитывать молекулярную массу, например, полимеров. Определив массу m или размер r макромолекулы, мольную массу (численно равную молекулярной массе) рассчитывают по формуле: 
 Экзаменационный билет № 19
Дисперсность является самостоятельным и полноправным термодинамическим параметром системы, а для дисперсных систем правило фаз Гиббса принимает следующий вид:  F – количество степеней свободы, К – количество компонентов, Ф – количество фаз. Р 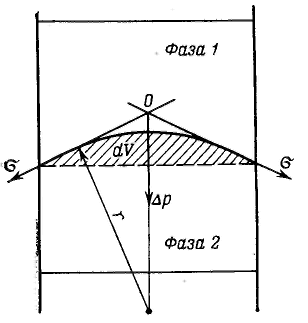 ассмотрим результат влияния кривизны поверхности раздела между двумя несмешивающимися жидкостями на внутреннее давление в фазах.Кривизна вызывает изменение площади и положения межфазной поверхности, что можно выразить приращением поверхностной энергии σds. Кроме того, изменяются объемы фаз V1 и V2 на dV1 и dV2. При условии постоянства объема всей системы dV1 = - dV2. Изменение объемов вызывает соответствующие изменения энергий фаз 1 и 2 на p1dV1 и p2dV2 (где p1 и р2 — давления внутри фаз). Соотношение между поверхностной энергией и «объемной» можно записать с помощью обобщенного уравнения первого и второго начал термодинамики относительно энергии Гельмгольца F при T=const:  При равновесии между фазами ΔF = 0, тогда  Это уравнение называется уравнением Лапласа. Для сферической поверхности  и уравнение принимает вид  .Капиллярные явления наблюдаются в содержащих жидкость узких сосудах (капилляры, капиллярно-пористые тела), у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание). Специфика поведения жидкости в капиллярных сосудах зависит от того, смачивает или не смачивает жидкость стенки сосуда, точнее, от значения краевого угла. Р 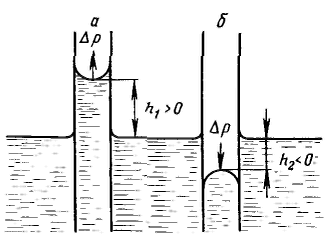 ассмотрим положение уровней жидкости в двух капиллярах, один из которых имеет лиофильную поверхность и поэтому стенки его смачиваются, у другого внутренняя поверхность лиофобизирована и не смачивается. В первом капилляре поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа стремится растянуть жидкость (давление направлено к центру кривизны) и поднимает ее в капилляре. Кривизна поверхности жидкости во втором капилляре положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотой h:  Чтобы высоту капиллярного поднятия связать с характеристикой смачивания, радиус мениска необходимо выразить через угол смачивания θ и радиус капилляра r0. На рисунке показан мениск жидкости в капилляре. Видно, что r0 = r·соsθ, тогда высоту капиллярного поднятия можно представить в виде формулы Жюрена:  Н 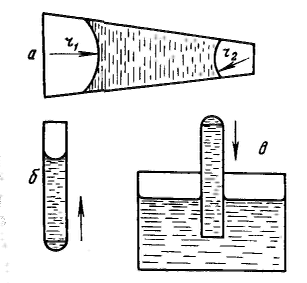 ередко приходится наблюдать, как жидкость не может вытечь из капилляра под действием силы тяжести. Это объясняется проявлением действия капиллярного потенциала, направленного против силы тяжести, так как на нижнем конце капилляра жидкость образует мениск с положительной кривизной. Если часть капилляра, находящаяся над жидкостью, меньше высоты поднятия жидкости, жидкость из него не вытекает, так как кривизна мениска жидкости вверху капилляра становится положительной (положительный радиус кривизны), отвечающей гидростатическому давлению столба жидкости, равному размеру (высоте) капилляра, т. е. устанавливается равновесие.
Основой доказательства теплового молекулярного движения в телах явилось обнаруженное английским ботаником Робертом Броуном в 1827 г. с помощью микроскопа непрерывное движете очень мелких частичек — спор папоротника (цветочной пыльцы), взвешенных в воде. Более крупные частицы находились в состоянии постоянного колебания около положения равновесия. Колебания и перемещения частиц ускорялись с уменьшением их размера и повышением температуры и не были связаны с какими-либо внешними механическими воздействиями. Теоретически обоснованная интерпретация броуновского движения — участие частиц дисперсной фазы ультрамикрогетерогенных систем в тепловом движении — была дана независимо друг от друга Эйнштейнии (1905 г.) и Смолуховским (1906 г.). П 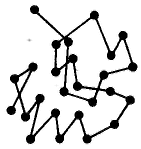 роведенными исследованиями была окончательно доказана природа броуновского движения. Молекулы среды (жидкости или газа) сталкиваются с частицей дисперсной фазы, в результате чего она получает огромное число ударов со всех сторон.Эйнштейн и Смолуховский для количественного выражения броуновского движения частиц ввели представление о среднем сдвиге частицы. Если при наблюдении движения частицы золя под микроскопом через определенные равные промежутки времени отмечать ее местонахождение, то можно получить ее траекторию движения. Так как движение происходит в трехмерном пространстве, то квадрат среднего расстояния, проходимого частицей за любой промежуток времени, равен  .Под микроскопам наблюдают проекцию смещения частицы на плоскость за какое-то время, поэтому  .При равновероятных отклонениях частицы ее направление будет находиться между направлениями x и у, т. е. под углом 45° к каждой координате. Отсюда  или  .Из-за равновероятных отклонений среднеарифметическое значение сдвигов равно нулю. Поэтому используются среднеквадратичные расстояния, проходимые частицей:  Эйнштейн и Смолуховский, постулируя единство природы броуновского движения и теплового движения, установили количественную связь между средним сдвигом частицы (называемым иногда амплитудой смещения) и коэффициентом диффузии D. Если броуновское движение является следствием теплового движения молекул среды, то можно говорить о тепловом движении частиц дисперсной фазы. Это означает, что дисперсная фаза, представляющая собой совокупность числа частиц, должна подчиняться тем же статистическим законам молекулярно-кинетической теории, приложимым к газам или растворам. Д 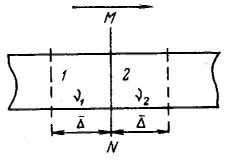 ля установления связи между средним сдвигом (смещением) частицы и коэффициентом диффузии представим себе трубку с поперечным сечением S, наполненную золем, концентрация частиц которого уменьшается слева направо. В этом же направлении протекает и диффузия частиц золя (на рисуике отмечено стрелкой). Выделим по обе стороны от линии MN два малых участка 1 и 2, размеры которых в направлении диффузии равны Δ — среднему квадратичному сдвигу за время τ. Обозначим частичную концентрацию золя в объемах этих участков соответственно через ν1 и ν2 (ν1>ν2). Хаотичность теплового движения приводит к равной вероятности переноса дисперсной фазы из обоих объемов вправо и влево от линии MN: половина частиц переместится вправо, а другая половина — влево. Количество дисперсной фазы за время τ переместится из объема 1 вправо:  , а из объема 2 влево (в обратном направлении): .Так как |Q1| > |Q2| (ν1>ν2), то суммарное количество перенесенного вещества через плоскость MN вправо определится соотношением  .Градиент концентрации по расстоянию в направлении диффузии можно выразить так:  Подставляя, получим:  Сравнивая это соотношение с первым законом диффузии Фика:  , окончательно имеем: Это уравнение выражает закон Эйнштейна — Смолуховского, в соответствии с которым квадрат среднего сдвига пропорционален коэффициенту диффузии н времени.
|