колды_ответы. Экзаменационный билет 1
 Скачать 3.42 Mb.
|
 Экзаменационный билет № 20
Термодинамическая реакционная способность характеризует способность вещества переходить в какое-либо иное состояние, например переходить в другую фазу, вступать в химическую реакцию. Она указывает на удаленность данного состояния вешества или системы компонентов от равновесного состояния при определенных условиях. Термодинамическая реакционная способность определяется химическим сродством, которое можно выразить изменением энергии Гиббса или разностью химических потенциалов. Реакционная способность зависит от степени дисперсности вещества, изменение которой может приводить к сдвигу фазового или химического равновесия. Соответствующее приращение энергии Гиббса dGд (благодаря изменению дисперсности) можно представить в виде объединенного уравнения первого и второго начал термодинамики:  Для индивидуального вещества V=Vм и при Т=const имеем:  Подставляя в это уравнение соотношение Лапласа, получим:  для сферической кривизны:  Если рассматривается переход вещества из конденсированной фазы в газообразную, то энергию Гиббса можно выразить через давление пара, приняв его за идеальный. Дополнительное изменение энергии Гиббса, связанное с изменением дисперсности, составляет:  Подставляя данное выражение, получим:  Полученное соотношение называется уравнением Кельвина (уравнение капиллярной конденсации). Для неэлектролитов его можно записать следующим образом:  Из этого уравнения видно, что с увеличением дисперсности растворимость растет, или химический потенциал частиц дисперсной системы больше, чем у крупной частицы, на величину 2σV/r. Степень дисперсности может влиять также на равновесие химической реакции:  С увеличением дисперсности повышается активность компонентов, а в соответствии с этим изменяется константа химического равновесия в ту или другую сторону, в зависимости от степени дисперсности исходных веществ и продуктов реакции. С изменением дисперсности веществ изменяется температура фазового перехода. Количественная взаимосвязь между температурой фазового перехода и дисперсностью вытекает из термодинамических соотношений. Для фазового перехода:  , Для сферических частиц:  Видно, что с уменьшением размера частиц г температуры плавления и испарения вещества уменьшаются (Hф.п.>0).
В золях через определенное, иногда очень длительное, время оседания частиц может наступить момент, когда диффузионный поток станет равным седиментационному iдиф = iсед, т.е. наступит диффузионно-седцментационное равновесие. Так как такое равновесие наступает при определенном градиенте концентраций, в системе должно установиться соответствующее распределение дисперсной фазы по высоте. Чтобы определить закон этого распределения, воспользуемся данным соотношением (iдиф = iсед), учтя, что  и заменив x на h (расстояние по высоте):  После разделения переменных получим:  Интегрируя в пределах от ν0 до νh и соответственно от h = 0 до h, найдем:  или  Это уравнение носит название гипсометрического закона (от лат. hypsos — высота). Если сравнить седиментацию при наличии диффузии и без нее, то обращает на себя внимание различие факторов, обеспечивающих устойчивость дисперсных систем к осаждению — седиментационную устойчивость. Эти факторы позволяют различать кинетическую седиментационную устойчивость (КСУ) и термодинамическую седиментационную устойчивость (ТСУ). Мерой кинетической седиментационной устойчивости является величина, обратная константе седиментации:  Мерой ТСУ является гипсометрическая высота. Ее удобнее определить как высоту he, на протяжении которой концентрация дисперсной фазы изменяется в е раз.  Данная формула показывает, что гипсометрическая высота и соответственно термодинамическая седиментационная устойчивость тем больше, чем меньше размер частиц и разность между плотностями частиц и среды. Вязкость не влияет на ТСУ, в то (же время повышение температуры способствует устойчивости, так как усиливается тепловое движение. Кинетическая же седиментационная устойчивость с повышением температуры обычно снижается в связи с уменьшением вязкости среды.
 Экзаменационный билет № 21
Закон Генри можно сформулировать следующим образом: при разбавлении системы (уменьшение давления) коэффициент распределения стремится к постоянному значению, равному константе распределении Генри. Относительно величины адсорбции А этот закон запишется так:  Э 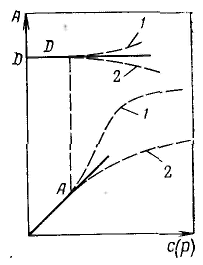 ти уравнения представляют собой изотермы адсорбции вещества при малых концентрациях. В соответствии с ними закон Генри можно сформулировать так: величина адсорбции при малых давлениях газа (концентрациях вещества в растворе) прямо пропорциональна давлению (концентрации).Отклонения от закона Генри, выражаемые изменениями коэффициентов активности в фазах, обычно не позволяют описать и прогнозировать ход изотерм с увеличением концентрации. (давления) адсорбата. Чтобы получить теоретическую изотерму адсорбции, описывающую более широкую область концентраций, необходимо использование представлений о механизме адсорбции и конкретных моделей. Большую долю отклонений коэффициента активности адсорбата в поверхностном слое от единицы можно учесть, используя представление об адсорбции как о квазихимической реакции между адсорбатом и адсорбционными центрами поверхности адсорбента. В этом заключается основная идея адсорбционной теории Ленгмюра. Это положение уточняется следующими допущениями: 1) адсорбция локализована (молекулы не перемещаются по поверхности) на отдельных адсорбционных центрах, каждый из которых взаимодействует только с одной молекулой адсорбата; в результате образуется мономолекулярный слой; 2) адсорбционные центры энергетически эквивалентны — поверхность адсорбента эквипотенциальна; 3) адсорбированные молекулы не взаимодействуют друг с другом. 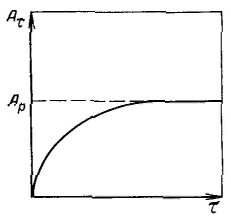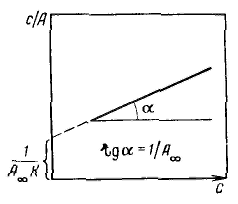Примем, что при адсорбции происходит квазихимическая реакция между распределяемым компонентом и адсорбционными центрами поверхности:  К  онстанта адсорбционного равновесия (без учета коэффициентов активности реагирующих веществ) равна: , где  После подстановки, получим:  О  кончательно имеем:  Это выражение называется уравнением изотермы мономолекулярной адсорбции Ленгмюра. Экспериментальные результаты по определению изотермы адсорбции обычно обрабатывают с помошью уравнения Ленгмюра, записанного в линейной форме: 
С 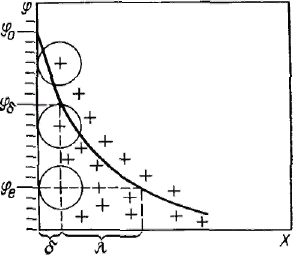 овременная теория строения двойного электрического слоя основана на представлениях Штерна. Она объединяет две предыдущие теории. Согласно современной теории слой противоионов состоит из двух частей.Одна часть примыкает непосредственно к межфазной поверхности и образует адсорбционный слои (слой Гельмгсиьца) толщиной δ, которая равна радиусу гидратированных ионов, его составляющих. Другая часть противононов находится в диффузной части — диффузный слой (слой Гуи) с потенциалом φδ, толщина λ которой может быть значительной и зависит от свойств и состава системы. Потенциал в диффузной части двойного электрического слоя не может зависеть линейно от расстояния, так как ионы в нем распределены неравномерно. В соответствии с принятыми представлениями потенциал в слое Гельмгольца при увеличении расстояния от слоя потенциалопределяющих ионов снижается до потенциала диффузного слоя линейно, а затем, как будет показано, по экспоненте. Теория Штерна учитывает также специфическую (некулоновскую, химическую) составляющую адсорбции ионов на поверхности раздела фаз, которая существенным образом может влиять на изменение потенциала. Пренебрежение размерами ионов приводит к тому, что не принимается во внимание толщина адсорбционною слон, и это, в свою очередь, вызывает большие погрешности при расчете параметров двойного электрического слоя. Кроме того, теория Гуи — Чепмена рассматривая только влияние концентрации и заряда ионов электролитов на изменение потенциала, не объясняет различного действия ионов разной природы, связанного со специфической адсорбцией их на межфазной поверхности. Штерн предложил рассматривать слой противоионов состоящим из двух частей: внутренней (плотный слой Гельмгольца) и внешней (диффузный слой). Таким образом, теорию Гуи — Чепмена можно использовать для описания только строения внешней части слоя, где можно пренебречь адсорбционными силами и размерами ионов. Внутреннюю (плотную) часть Штерн представил как адсорбционный моноионный слой, в котором противоионы примыкают к поверхности благодаря электростатическим силам и специфическому взаимодействию. Введенный Штерном потенциал φδ часто называют штерновским. В плотной части двойного электрического слоя потенциал уменьшается линейно от φ0 до φδ. Принимая текущими переменными φ и х вместо φδ и δ, получим:  Штерн попытался учесть влияние специфической адсорбции ионов на электрический потенциал, обусловленный действием ковалентных сил дополнительно к электростатическим силам. Так как радиус действия сил такой адсорбции соизмерим с размером ионов, это дает основание учитывать копалентные силы только для ионов, входящих в плотный слой Гельмгольца. Как видно из рисунка, плотность поверхностного заряда противоионов можно разделить на две части: плотность заряда qГ, обусловленного моноионным слоем, представляющим собой слой Гельмгольца, и плотность заряда qδ диффузного слоя Гуи. Общая поверхностная плотность заряда двойного электрического слоя равна сумме поверхностных плотностей зарядов плотного и диффузного слоев с обратным знаком:  По Штерну, заряд слоя Гельмгольца складывается из заряда ионов, адсорбированых как за счет электростатического адсорбционного потенциала Fzφ, так и за счет потенциала специфической адсорбции Ф. Было предположено, что поверхность имеет определенное число адсорбционных центров, каждый из которых взаимодействует с одним противоионом. Пример образования ДЭС: Д 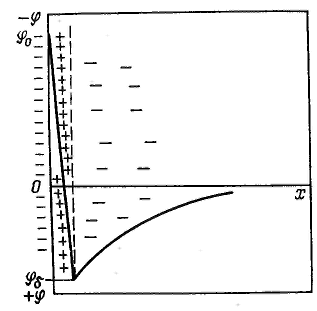 обавление в систему металл — вода раствора хлорида натрия приводит к избирательной адсорбции хлорид-анионов на поверхности металла. Появляется избыточный отрицательный заряд на поверхности металла и избыточный положительный заряд (ионы натрия) в близлежащем слое раствора, т. е. на межфазной поверхности образуется двойной электрический слой.Сильно адсорбирующиеся ионы в плотном слое иногда способны не только полностью скомпенсировать поверхностный потенциал, но и создать избыточный заряд со знаком заряда противоионов. Это явление называется перезарядкой. Перезарядка приводит к смене противоионов в диффузном слое на ионы с зарядом другого знака. На рисунке видно, что при перезарядке поверхностный потенциал φ0 и потенциал диффузного слоя φδ имеют разные знаки. На формирование двойного электрического слоя существенное влияние оказывает природа поверхности конденсированной фазы, наличие определенных ионов в растворе, их концентрация. Рассмотрим систему водный раствор — поверхность иодида серебра. При избытке в растворе ионов серебра, например при добавлении нитрата серебра, эти ионы являются потенцналопределяюшими. В роли противоионов выступают нитрат-ионы, часть которых находится в плотном слое, а другая часть — в диффузном слое. Для такой системы формулу двойного электрического слоя можно записать следующим образом:  В дисперсных системах двойной электрический слой возникает на поверхности частиц. Частицу дисперсной фазы в гетерогенно-дисперсной системе вместе с двойным электрическим слоем называют мицеллой. Строение мицеллы можно показать той же формулой, что и строение двойного электрического слоя. Внутреннюю часть мицеллы составляет агрегат основного вещества. На поверхности агрегата расположены потенциалопре-деляющие ионы. Агрегат вместе с потенциалопределяющими ионами составляет ядро мицеллы. Ядро с противоионами плотной части двойного электрического слоя образуют гранулу. Гранулу окружают противоионы диффузного слоя. Мицелла в отличие от гранулы электронейтральна. {(AgI)mnAg+|(n-x)NO3-}xNO3-
 Экзаменационный билет № 22
Уравнение Ленгмюра можно использовагь только при условии, что адсорбция вещества сопровождается образованием мономолекулярного слоя. В большинстве случаев мономолекулярный адсорбционный слой не компенсирует полностью избыточную поверхностную энергию и влияние поверхностных сил может распространяться на второй, третий и последующие адсорбционные слои, в результате проходит полимолекулярная адсорбция. С 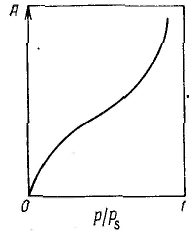 овременная форма уравнения полимолекулярной адсорбции — основного уравнения обобщенной теории Ленгмюра — была предложена Брунауэром, Эмметом и Теллером.В этой теории дополнительным допущением к тем, которые были положены в основу вывода уравнения изотермы Ленгмюра, является представление об образовании на поверхности адсорбента «последовательных комплексов» адсорбционных центров с одной, двумя, тремя и т. д. молекулами адсорбата. Тогда процесс адсорбции можно представить в виде последовательных квазихимических реакций:  Константы равновесия этих реакций соответственно равны  Обозначим:  Общее число активных центров на адсорбенте, или емкость монослоя, будет равна 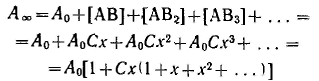 После ряда вычислений с применением теории рядов, окончательно получим:  Д 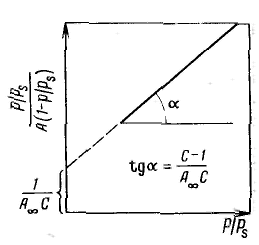 анное соотношение является основным уравнением обобщенной теории Ленгмюра и называется уравнением полимолекулярной адсорбции БЭТ.При обработке экспериментальных результатов уравнение БЭТ обычно используют в линейной форме:  Оно позволяет графически определить оба постоянных параметра A∞ и С: Экспериментальное определение A∞ позволяет рассчитать удельную поверхность адсорбента (поверхность единицы массы адсорбента):  .
Все дисперсные системы в зависимости от механизма процесса их образования по классификации П. А. Ребиндера подразделяют на лиофильные, которые получаются при самопроизвольном диспергировании одной из фаз (самопроизвольное образование гетерогенной свободнодисперсной системы), и лиофобные, получающиеся в результате диспергирования и конденсации с пересыщением (принудительное образование гетерогенной свободноднсперсной системы). Если с увеличением концентрации вещества поверхностное натяжение на границе раздела фаз понижается, то такое вещество называют поверхностно-активным. Для таких веществ поверхностная активность  Наличие гидрофильной и олеофильной частей у молекул ПАВ является характерной отличительной особенностью их строения. По способности к диссоциации в водных растворах поверхностно-активные вещества делят на ионогенные и неионогенные. В свою очередь ионогенные ПАВ подразделяют на анионные, катионные и амфолитпые (амфотерные). 1) Анионные ПАВ диссоциируют в воде с образованием поверхностно-активного аниона. 2) Катионные ПАВ диссоциируют в воде с образованием поверхностно-активного катиона. 3) Амфолитные ПАВ содержат две функциональные группы, одна из которых имеет кислый, а другая основный характер, например карбоксильную и аминную группы. В зависимости от рН среды амфолитные ПАВ проявляют анионоактивные или катионоактивные свойства. Все ПАВ относительно поведения их в воде делят на истинно растворимые и коллоидные. Истинно растворимые ПАВ в растворе находятся в молекулярно-дисперсном состоянии вплоть до концентраций, соответствующих их насыщенным растворам и разделению системы на две сплошные фазы. Главной отличительной особенностью коллоидных ПАВ является способность образовывать термодинамически устойчивые (лиофильные) гетерогенные дисперсные системы (ассоциативные, или мицеллярные, коллоиды). К основным свойствам коллоидных ПАВ, обусловливающим их ценные качества и широкое применение, относятся высокая поверхностная активность; способность к самопроизвольному мицеллообразованию — образованию лиофильных коллоидных растворов при концентрации ПАВ выше некоторого определенного значения, называемого критической концентрацией мицеллообразования (KKM); способность к солюбилизации — резкому увеличению растворимости веществ в растворах коллоидных ПАВ вследствне их «внедрения» внутрь мицеллы; высокая способность стабилизировать различные дисперсные системы. При концентрациях выше KKM молекулы ПАВ собираются в мицеллы (ассоциируют) и раствор перехолит в мицеллярную (ассоциативную) коллоидную систему. Под мицеллой ПАВ понимают ассоциат дифильных молекул, лиофильные группы которых обращены к соответствующему растворителю, а лиофобные группы соединяются друг с другом, образуя ядро мицеллы. Число молекул, составляющих мицеллу, называют числом ассоциации, а общую сумму молекулярных масс молекул в мицелле, или произведение массы мицеллы на число Авогадро, — мицеллярной массой. Определенное ориентирование дифильных молекул ПАВ в мицелле обеспечивает минимальное межфазное натяжение на границе мицелла — среда. П 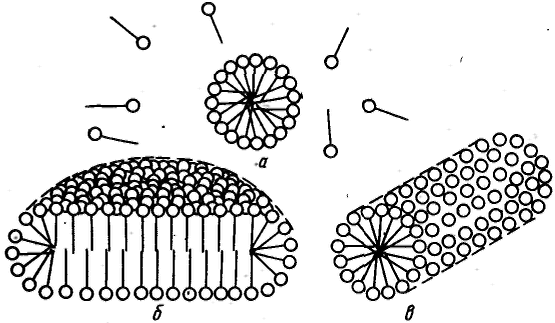 ри концентрациях ПАВ в водном растворе, несколько превышающих KKM, согласно представлениям Гартли образуются сферические мицеллы (мицеллы Гартли). Внутренняя часть мицелл Гартли состоит из переплетающихся углеводородных радикалов, полярные группы молекул ПАВ обращены в водную фазу. Диаметр таких мицелл равен удвоенной длине молекул ПАВ. Число молекул в мицелле быстро растет в пределах узкого интервала концентраций, а при дальнейшем увеличении концентрации практически не изменяется, а увеличивается число мицелл. Сферические мицеллы могут содержать от 20 до 100 молекул и более.При увеличении концентрации ПАВ мицеллярная система проходит ряд равновесных состояний, различающихся по числам ассоциации, размерам и форме мицелл. При достижении определенной концентрации сферические мицеллы начинают взаимодействовать между собой, что способствует их деформации. Мицеллы стремятся принять цилиндрическую, дискообразную, палочкообразную, пластинчатую форму. Мицеллообразование в неводных средах, как правило, является результатом действия сил притяжения между полярными группами ПАВ и взаимодействия углеводородных радикалов с молекулами растворителя. Образующиеся мицеллы обращенного вида содержат внутри негидратированные или гидратированные полярные группы, окруженные слоем из углеводородных радикалов. Число ассоциации (от 3 до 40) значительно меньше, чем для водных растворов ПАВ. Как правило, оно растет с увеличением углеводородного радикала до определенного предела. Явление растворения веществ в мицеллах ПАВ называется солюбилизацией. Способ включения молекул солюбилизата в мицеллы в водных растворах зависит от природы вещества. Неполярные углеводороды, внедряясь в мицеллы, располагаются в углеводородных ядрах мицелл. Полярные органические вещества (спирты, амины, кислоты) встраиваются в мицеллу между молекулами ПАВ так, чтобы их полярные группы были обращены к воде, а липофильные части молекул ориентированы параллельно углеводородным радикалам ПАВ. Возможен и третий способ включения солюбилизата в мицеллы, особенно характерный для неионогенных ПАВ. Молекулы солюбилизата, например фенола, не проникают внутрь мицелл, а закрепляются на их поверхности, располагаясь между беспорядочно изогнутыми полиоксиэтиленовыми цепями. Солюбилизация — самопроизвольный и обратимый процесс; данной концентрации ПАВ и температуре соответствует вполне определенное насыщение раствора солюбилизатом. В результате солюбилизации получаются устойчивые дисперсные системы подобные самопроизвольно образующимся ультрамнкрогетерогенным эмульсиям.
 Экзаменационный билет № 23
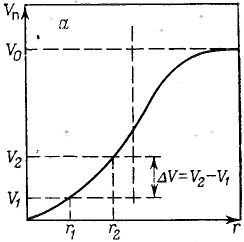
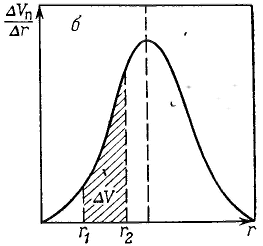
Удерживание газов и паров пористыми телами, т. е. их адсорбционная способность, зависят как от природы взаимодействующих тел, так и от структуры пористого тела. Если структурный фактор для макропористых адсорбентов имеет малое значение, то уже для переходнопористых тел его роль резко возрастает. Это обусловлено в первую очередь проявлением капиллярных сил. Чем меньше размер пор, тем сильнее капиллярное удерживание адсорбата. В противном случае (если поверхность не смачивается) наблюдается капиллярное выталкивание вещества из пор, адсорбция на несмачиваемых телах минимальна и возможна только на ровной поверхности и в крупных порах. Адсорбция на переходнопористых телах происходит в основном по механизму капиллярной конденсации. Капиллярная конденсация начинает проявляться при определенной степени заполнения адсорбента или при определенном значении давления пара, характерном для данной системы. Д 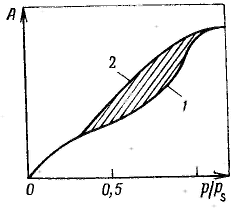 ля адсорбентов с переходными порами характерна изотерма адсорбции с петлей капиллярно-конденсационного гистерезиса. Адсорбции соответствует нижняя кривая, а десорбции — верхняя. При малых давлениях, когда не происходит капиллярная конденсация, гистерезиса не наблюдается. Начало появления гистерезиса зависит от природы адсорбента и адсорбата.К 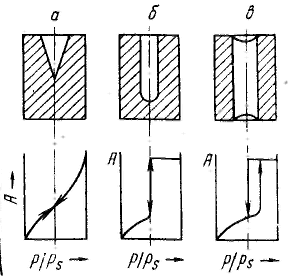 онденсация на стенках цилиндрической поры приводит к уменьшению диаметра поры, что вызывает ее мгновенное заполнение при давлении, отвечающем началу конденсации. На концах поры образуются сферические мениски жидкости. Десорбция может начаться только при давлении, соответствующем радиусам кривизны этих менисков. Таким образом, опорожнение капилляра происходит при меньшем давлении, чем его заполнение. Этим объясняется появление петли капиллярно-конденсационного гистерезиса.Капиллярная конденсация описывается уравнением Кельвина, в которое входит радиус кривизны мениска, и это позволяет использовать его для расчета функции распределения пор по размерам. Метод расчета функций распределения частиц (пор) по размерам заключается в построении интегральных и дифференциальных кривых распределения. Для пористых тел принято характеризовать распределение пор по их радиусам, поэтому интегральная кривая распределения выражает зависимость общего объема пор от их радиуса:  .Другой функцией распределения для данного пористого тела является зависимость f(rп) или dVп/drп от rп, которая называется дифференциальной кривой распределения. Она более четко и наглядно характеризует полидисперсность системы.
|
