колды_ответы. Экзаменационный билет 1
 Скачать 3.42 Mb.
|
|
Экзаменационный билет № 1
Коллоидная химия – физическая химия поверхностных явлений и дисперсных систем. Признаки коллоидных систем:
Гетерогенность количественно определяется поверхностным натяжением — величиной, характеризующей энергию единицы поверхности и являющейся фактором интенсивности. Поверхностное натяжение определяет как бы степень гетерогенности, резкость перехода от одной фазы к другой, различие между соприкасающимися фазами. Чем сильнее выражена гетерогенность и чем более резко различаются по природе сопряженные фазы, тем больше поверхностное натяжение. Отсутствие гетерогенности равнозначно отсутствию поверхностного натяжения. Гетерогенным системам присуща поверхностная энергия: G = σ·s. Второй признак — дисперсность. Дисперсность – величина, обратная поперечному размеру частиц: D=1/а. Системы с малой дисперсностью (менее 103 см-1) не принято рассматривать как коллоидные. Широко применяется и третья характеристика раздробленности — удельная поверхность Sуд, определяемая отношением площади межфазной поверхности к объему тела s/V, Все три характеристики раздробленности связаны между собой: с уменьшением размера а увеличиваются дисперсность D и удельная поверхность Sуд. Классификация по кинетическим свойствам:
Классификация по размеру частиц:
Коллоидные явления широко распространены в химической технологии. Практически нет такого химического производства, которое бы не осуществлялось с участием поверхностных явлений и дисперсных систем. Измельчение сырья и промежуточных продуктов, обогащение, в том числе флотация, сгущение, отстаивание и фильтрация, конденсация, кристаллизация и вообще процессы образования новых фаз, брикетирование, спекание, гранулирование — все эти процессы протекают в дисперсных системах, и в них большую роль играют такие коллоидно-химические явления, как смачивание, капиллярность, адсорбция, седиментация, коагуляция. Большое распространение в химической технологии получили адсорбенты и катализаторы, которые представляют собой дисперсные системы с твердой дисперсионной средой. Адсорбция имеет самостоятельное значение для очистки и разделения веществ, извлечения ценных компонентов, хроматографии и др. Как правило, все гетерогенные процессы в химической технологии для увеличения их скорости проводят при максимальной поверхности контакта фаз. Это значит, что системы в реакционных аппаратах находятся в состоянии суспензий, паст, пульп, эмульсий, пен, порошков, туманов, пылей. Несмотря на то что толщина поверхностных слоев не превышает несколько молекул, их роль не менее важна, чем объемных фаз, например, в процессах массопередачи (адсорбция, экстракция, сушка, испарение и др.), термоэлектронной эмиссии, смазочном действии, адгезии.
Все электрические свойства межфазных поверхностей и явления, протекающие на них, обусловлены наличием двойного электрического слоя на границе раздела фаз. Количественные связи между параметрами двойного электрического слоя определяются его строением. Первые предположения об образовании двойного электрического слоя были сделаны Квинке. Строение двойного электрического слоя впервые было представлено Гельмгольцем и Перреном по аналогии со строением плоского конденсатора. Согласно их представлениям, на границе соприкасающихся фаз заряды располагаются в виде двух рядов разноименных ионов: ряд потенциалопредвляющих ионов на расстоянии, равном их радиусу в несольватированном состоянии, и прилегающий к нему ряд противоионов. Толщина электрического слоя близка к молекулярным размерам или размерам сольватированных ионов. Потенциал слоя снижается в пределах его толщины линейно до нуля. Поверхностный заряд qs определяется в соответствии с теорией плоского конденсатора уравнением:  Вполне естественно, что подобное строение двойного слоя возможно при отсутствии теплового движения ионов. В реальных же условиях распределение зарядов на границе раздела фаз в первом приближении определяется соотношением сил электростатического притяжения ионов, зависящего от электрического потенциала φ0 и теплового движения ионов, стремящихся равномерно распределиться во всем объеме жидкой или газообразной фазы. К такому выводу независимо друг от друга пришли Гуи и Чепмен. Они предположили, что двойной электрический слой имеет диффузное (размытое) строение и все противоионы находятся в диффузной его части — в диффузном слое. Поскольку протяженность диффузного слоя определяется кинетической энергией ионов, то в области температур, близких к абсолютному нулю, все противоионы будут находиться в непосредственной близости к потенциалопределяющим ионам. С 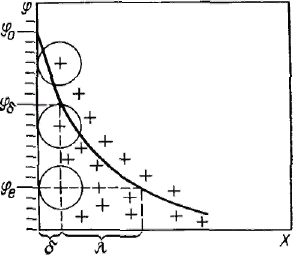 овременная теория строения двойного электрического слоя основана на представлениях Штерна. Она объединяет две предыдущие теории. Согласно современной теории слой противоионов состоит из двух частей.Одна часть примыкает непосредственно к межфазной поверхности и образует адсорбционный слои (слой Гельмгсиьца) толщиной δ, которая равна радиусу гидратированных ионов, его составляющих. Другая часть противононов находится в диффузной части — диффузный слой (слой Гуи) с потенциалом φδ, толщина λ которой может быть значительной и зависит от свойств и состава системы. Потенциал в диффузной части двойного электрического слоя не может зависеть линейно от расстояния, так как ионы в нем распределены неравномерно. В соответствии с принятыми представлениями потенциал в слое Гельмгольца при увеличении расстояния от слоя потенциалопределяющих ионов снижается до потенциала диффузного слоя линейно, а затем, как будет показано, по экспоненте. Теория Штерна учитывает также специфическую (некулоновскую, химическую) составляющую адсорбции ионов на поверхности раздела фаз, которая существенным образом может влиять на изменение потенциала. Уравнение Пуассона — Больцмана:  Это уравнение после двойного интегрирования дает соотношение, выражающее закон изменения поверхностного потенциала от расстояния в диффузной части двойного электрического слоя и от свойств раствора. Чтобы в полной мере представлять возможности этого соотношения, лежащего в основе теории двойного электрического слоя, необходимо учитывать основные допущения и предположения, принятые Гуи и Чепменом при его выводе: двойной электрический слой является плоским, диэлектрическая проницаемость не зависит от расстояния х, ионы представляют собой точечные заряды (т. е. не имеют объема), при переводе противоионов из объема раствора в двойной электрический слой совершается работа только против электростатических сил. Обычно уравнение Пуассона — Больцмана решают применительно к конкретным граничным условиям. Ниже приводится его решение при условии малости потенциала диффузного слоя (φδ<<25 мВ). Обозначим экспоненциальный показатель у фактора Больцмана через у. При малых значениях φ и соответственно y<<1 фактор Больцмана можно разложить в ряд Маклорена:  Если ограничиться двумя первыми членами ряда, то уравнение для объемной плотности заряда после этих преобразований примет вид:  Первый член правой части этого уравнения равен нулю. так как он включает сумму зарядов в объеме раствора, которая по условиям электронейтральности равна нулю, и поэтому окончательно имеем:  После такого преобразования уравнение Пуассона — Больцмана принимает следующую форму:  Выражение æ2 перед φх включает постоянные, характеризующие свойства раствора, поэтому можно считать, что они не изменяются с расстоянием от поверхности:  Окончательно имеем:  Если расстояние х отсчитывать от начала диффузной части двойного электрического слоя, то  Последние уравнения называются уравнениями Гуи-Чепмена, из них следует, что потенциал в области диффузного слоя в зависимости от расстояния уменьшается по экспоненте.
|