Экзаменационные билеты по коллоидной химии. Экзаменационный билет 1
 Скачать 3.47 Mb.
|
|
Общее определение поверхностной активности дается соотношением:  которое справедливо как для неэлектролитов, так и для электролитов. Поверхностная активность, как и гиббсовская адсорбция, может быть положительной и отрицательной. Абсолютное значение и ее знак зависят от природы как адсорбируемого вещества, так и среды (растворителя). Если с увеличением концентрации вещества поверхностное натяжение на границе раздела фаз понижается, то такое вещество называют поверхностно-активным. Для таких веществ  Вещества, повышающие поверхностное натяжение на границе раздела фаз с увеличением концентрации, называют поверхностно-инактивными. Для них 
С  овременная теория строения двойного электрического слоя основана на представлениях Штерна. Она объединяет две предыдущие теории. Согласно современной теории слой противоионов состоит из двух частей.Одна часть примыкает непосредственно к межфазной поверхности и образует адсорбционный слои (слой Гельмгсиьца) толщиной δ, которая равна радиусу гидратированных ионов, его составляющих. Другая часть противононов находится в диффузной части — диффузный слой (слой Гуи) с потенциалом φδ, толщина λ которой может быть значительной и зависит от свойств и состава системы. Потенциал в диффузной части двойного электрического слоя не может зависеть линейно от расстояния, так как ионы в нем распределены неравномерно. В соответствии с принятыми представлениями потенциал в слое Гельмгольца при увеличении расстояния от слоя потенциалопределяющих ионов снижается до потенциала диффузного слоя линейно, а затем, как будет показано, по экспоненте. Теория Штерна учитывает также специфическую (некулоновскую, химическую) составляющую адсорбции ионов на поверхности раздела фаз, которая существенным образом может влиять на изменение потенциала. Пренебрежение размерами ионов приводит к тому, что не принимается во внимание толщина адсорбционною слон, и это, в свою очередь, вызывает большие погрешности при расчете параметров двойного электрического слоя. Кроме того, теория Гуи — Чепмена рассматривая только влияние концентрации и заряда ионов электролитов на изменение потенциала, не объясняет различного действия ионов разной природы, связанного со специфической адсорбцией их на межфазной поверхности. Штерн предложил рассматривать слой противоионов состоящим из двух частей: внутренней (плотный слой Гельмгольца) и внешней (диффузный слой). Таким образом, теорию Гуи — Чепмена можно использовать для описания только строения внешней части слоя, где можно пренебречь адсорбционными силами и размерами ионов. Внутреннюю (плотную) часть Штерн представил как адсорбционный моноионный слой, в котором противоионы примыкают к поверхности благодаря электростатическим силам и специфическому взаимодействию. Введенный Штерном потенциал φδ часто называют штерновским. В плотной части двойного электрического слоя потенциал уменьшается линейно от φ0 до φδ. Принимая текущими переменными φ и х вместо φδ и δ, получим:  Штерн попытался учесть влияние специфической адсорбции ионов на электрический потенциал, обусловленный действием ковалентных сил дополнительно к электростатическим силам. Так как радиус действия сил такой адсорбции соизмерим с размером ионов, это дает основание учитывать копалентные силы только для ионов, входящих в плотный слой Гельмгольца. Как видно из рисунка, плотность поверхностного заряда противоионов можно разделить на две части: плотность заряда qГ, обусловленного моноионным слоем, представляющим собой слой Гельмгольца, и плотность заряда qδ диффузного слоя Гуи. Общая поверхностная плотность заряда двойного электрического слоя равна сумме поверхностных плотностей зарядов плотного и диффузного слоев с обратным знаком:  По Штерну, заряд слоя Гельмгольца складывается из заряда ионов, адсорбированых как за счет электростатического адсорбционного потенциала Fzφ, так и за счет потенциала специфической адсорбции Ф. Было предположено, что поверхность имеет определенное число адсорбционных центров, каждый из которых взаимодействует с одним противоионом. Пример образования ДЭС: Д  обавление в систему металл — вода раствора хлорида натрия приводит к избирательной адсорбции хлорид-анионов на поверхности металла. Появляется избыточный отрицательный заряд на поверхности металла и избыточный положительный заряд (ионы натрия) в близлежащем слое раствора, т. е. на межфазной поверхности образуется двойной электрический слой.Сильно адсорбирующиеся ионы в плотном слое иногда способны не только полностью скомпенсировать поверхностный потенциал, но и создать избыточный заряд со знаком заряда противоионов. Это явление называется перезарядкой. Перезарядка приводит к смене противоионов в диффузном слое на ионы с зарядом другого знака. На рисунке видно, что при перезарядке поверхностный потенциал φ0 и потенциал диффузного слоя φδ имеют разные знаки. На формирование двойного электрического слоя существенное влияние оказывает природа поверхности конденсированной фазы, наличие определенных ионов в растворе, их концентрация. Рассмотрим систему водный раствор — поверхность иодида серебра. При избытке в растворе ионов серебра, например при добавлении нитрата серебра, эти ионы являются потенцналопределяюшими. В роли противоионов выступают нитрат-ионы, часть которых находится в плотном слое, а другая часть — в диффузном слое. Для такой системы формулу двойного электрического слоя можно записать следующим образом:  В дисперсных системах двойной электрический слой возникает на поверхности частиц. Частицу дисперсной фазы в гетерогенно-дисперсной системе вместе с двойным электрическим слоем называют мицеллой. Строение мицеллы можно показать той же формулой, что и строение двойного электрического слоя. Внутреннюю часть мицеллы составляет агрегат основного вещества. На поверхности агрегата расположены потенциалопре-деляющие ионы. Агрегат вместе с потенциалопределяющими ионами составляет ядро мицеллы. Ядро с противоионами плотной части двойного электрического слоя образуют гранулу. Гранулу окружают противоионы диффузного слоя. Мицелла в отличие от гранулы электронейтральна. {(AgI)mnAg+|(n-x)NO3-}xNO3-
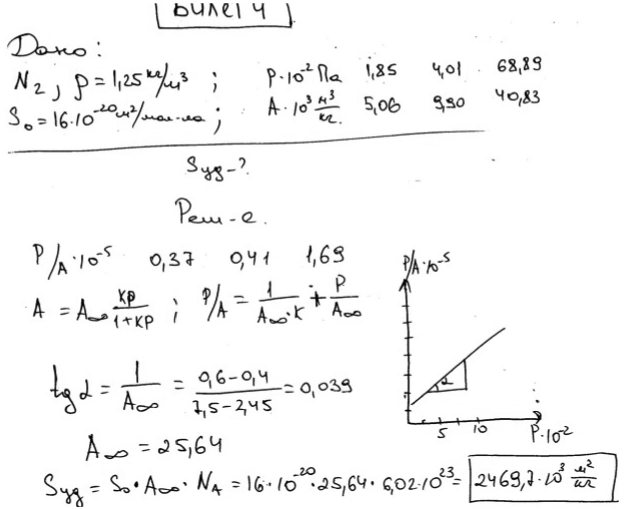
Экзаменационный билет № 4
Адгезия, смачивание и растекание относятся к межфазным взаимодействиям, которые происходят между конденсированными фазами. Межфазное взаимодействие, или взаимодействие между приведенными в контакт поверхностями конденсированных тел разной природы, называют адгезией (прилипанием). Работа адгезии Wа, характеризующая прочность адгезионной связи, определяется работой обратимого разрыва адгезионной связи, отнесенной к единице площади. Ома измеряется в тех же единицах, что и поверхностное натяжение (Дж/м2). Полная работа адгезии, приходящаяся на всю площадь контакта тел s, равна  Ч  тобы получить соотношение между работой адгезии и поверхностными натяжениями взаимодействующих компонентов, представим себе две конденсированные фазы 2 и 3, имеющие поверхности на границе с воздухом 1, равные единице площади. Для начального и конечного состояний системы имеем  Изменение энергии Гиббса системы в процесс адгезии равно  или  Это уравнение Дюпре. Оно отражает закон сохранения энергии при адгезии. Условие растворения:  Смачивание— это поверхностное явление, заключающееся во взаимодействии жидкости с твердым или другим жидким телом при наличии одновременного контакта трех несмешивающихся фаз, одна из которых обычно является газом (воздухом). Степень смачивания количественно характеризуется косинусом краевого угла (угла смачивания), или просто краевым углом (углом смачивания). У 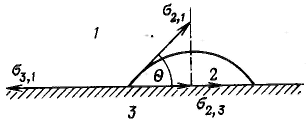 гол θ, который образован касательными к межфазным поверхностям, ограничивающим смачивающую жидкость, имеющий вершину на линии раздела трех фаз, называется краевым углом, или углом смачивания.Так как поверхностное натяжение можно рассматривать как энергию, приходящуюся на единицу площади, или как силу, действующую на единицу длины, то все рассмотренные составляющие поверхностной энергии можно выразить с помощью векторов сил. При равновесии между ними соблюдается следующее соотношение:  Полученное соотношение называется законом Юнга. Чем меньше угол Θ и соответственно больше cos θ, тем лучше смачивается поверхность. При остром угле Θ, т. е. при cos θ>0, поверхность считают хорошо смачиваемой данной жидкостью. Если угол θ тупой, т. е. соs θ<0, то по отношению к данной жидкости поверхность смачивается плохо (часто говорят «не смачивается»). Уравнение Дюпре самостоятельно почти не используется для расчета работы адгезии из-за трудности определения поверхностного натяжения твердых тел на границе с газом (воздухом) и жидкостью. Удобную для расчета этой величины форму имеет соотношение, получаемое в результате сочетания уравнения Дюпре с законом Юнга Если разность  в уравнении Дюпре заменить ее выражением нз закона Юнга , получим Это уравнение называют уравнением Дюпре-Юнга; оно связывает работу адгезии с краевым углом и позволяет рассчитать работу адгезии, если известны поверхностное натяжение жидкости и краевой угол. Обе эти величины можно сравнительно легко определить экспериментально. Введение ПАВ уменьшает работу когезии (поверхностное натяжение) жидкости а значит, как следует из уравнения Дюпре-Юнга, увеличивает смачивание. Лучше смачивает та жидкость, которая имеет меньшее поверхностное натяжение или работу когезии.
Протекание электрокинетических явлений в дисперсных систе-иах возможно при наличии на границе раздела фаз двойного электрического слоя, имеющего диффузное строение. При относительном перемещении фаз независимо от причин, его вызвавших, происходит разрыв двойного электрического слоя по плоскости скольжения. Потенциал, возникающий на плоскости скольжения при отрыае части диффузного слоя, называется электрокинетическим потенциалом или ζ (дзета)-потенциалом. Для получения наиболее простого уравнения, связывающего скорость относительного движения фаз с параметрами дисперсионной среды (вязкость, диэлектрическая проницаемость), двойного электрического слоя (ζ-потенциал) и внешнего электрического поля (напряженность), необходимо задаться некоторыми ограничениями: 1) толщина двойного электрического слоя значительно меньше радиуса пор, капилляров твердой фазы (радиуса кривизны поверхности твердой фазы); 2) слой жидкости, непосредственно прилегающий к твердой фазе, неподвижен, движение жидкости в порах твердой фазы ламинарное и подчиняется законам гидродинамики; 3) распределение зарядов в двойном электрическом слое не зависит от приложенной разности потенциалов; 4) твердая фаза является диэлектриком, а жидкость проводит электрический ток. Электрическая сила, действующая на слой жидкости dх (в расчете на единицу площади поверхности), равна  Сила трения и ее дифференциал, приходящиеся на единиц) площади (согласно закону Ньютона), составляют:  При установившемся движении (в стационарном состоянии) dFэл = dFтр:  После интегрирования, окончательно получим следующее выражение для постоянной линейной скорости жидкости относительно мембраны:  Это уравнение носит название уравнения Гельмгольца — Смолуховского. Уравнение Гельмгольца — Смолуховского чаще записывают относительно ζ-потенциала:  Это дифференциальное уравнение справедливо как для электроосмоса, так и для электрофореза, поскольку оно было выведено из баланса движущих сил процесса — электрической силы и силы трения. Отличие состоит только в выбранной системе координат. Несовпадение экспериментальных и теоретических значений электрофоретнческой подвижности определяется в основном двумя эффектами, неучтенными теорией Гельмгольца — Смолуховского: релаксационным эффектом и электрофоретическим торможением. Релаксационный эффект проявляется в нарушении симметрии диффузного слоя вокруг частицы при относительном движении фаз в противоположные стороны. Возникает внутреннее электрическое поле (диполь), направленное против внешнего поля. Для восстановления равновесного состояния системы требуется некоторое время, называемое временем релаксации. Электрофоретическое торможение обусловлено сопротивлением движению частицы обратным потоком противоионов, который увлекает за собой жидкость. Вследствие этого электрофоретическая скорость уменьшается.
 Экзаменационный билет № 5
Дисперсность является самостоятельным и полноправным термодинамическим параметром системы, а для дисперсных систем правило фаз Гиббса принимает следующий вид:  F – количество степеней свободы, К – количество компонентов, Ф – количество фаз. Р 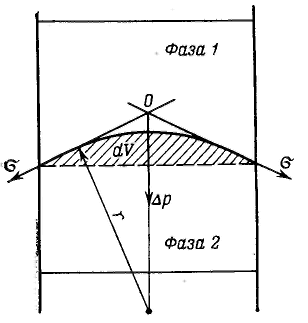 ассмотрим результат влияния кривизны поверхности раздела между двумя несмешивающимися жидкостями на внутреннее давление в фазах.Кривизна вызывает изменение площади и положения межфазной поверхности, что можно выразить приращением поверхностной энергии σds. Кроме того, изменяются объемы фаз V1 и V2 на dV1 и dV2. При условии постоянства объема всей системы dV1 = - dV2. Изменение объемов вызывает соответствующие изменения энергий фаз 1 и 2 на p1dV1 и p2dV2 (где p1 и р2 — давления внутри фаз). Соотношение между поверхностной энергией и «объемной» можно записать с помощью обобщенного уравнения первого и второго начал термодинамики относительно энергии Гельмгольца F при T=const:  При равновесии между фазами ΔF = 0, тогда  Это уравнение называется уравнением Лапласа. Для сферической поверхности  и уравнение принимает вид  .Капиллярные явления наблюдаются в содержащих жидкость узких сосудах (капилляры, капиллярно-пористые тела), у которых расстояние между стенками соизмеримо с радиусом кривизны поверхности жидкости. Кривизна возникает в результате взаимодействия жидкости со стенками сосуда (адгезия, смачивание). Специфика поведения жидкости в капиллярных сосудах зависит от того, смачивает или не смачивает жидкость стенки сосуда, точнее, от значения краевого угла. Р 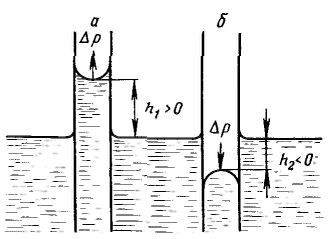 ассмотрим положение уровней жидкости в двух капиллярах, один из которых имеет лиофильную поверхность и поэтому стенки его смачиваются, у другого внутренняя поверхность лиофобизирована и не смачивается. В первом капилляре поверхность жидкости имеет отрицательную кривизну, поэтому дополнительное давление Лапласа стремится растянуть жидкость (давление направлено к центру кривизны) и поднимает ее в капилляре. Кривизна поверхности жидкости во втором капилляре положительна, дополнительное давление направлено внутрь жидкости, в результате жидкость в капилляре опускается (отрицательное капиллярное поднятие). При равновесии лапласовское давление равно гидростатическому давлению столба жидкости высотой h:  Чтобы высоту капиллярного поднятия связать с характеристикой смачивания, радиус мениска необходимо выразить через угол смачивания θ и радиус капилляра r0. На рисунке показан мениск жидкости в капилляре. Видно, что r0 = r·соsθ, тогда высоту капиллярного поднятия можно представить в виде формулы Жюрена:  Н 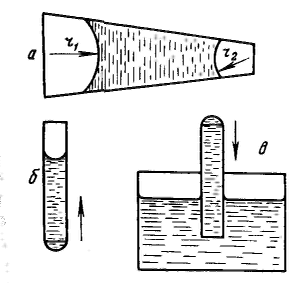 ередко приходится наблюдать, как жидкость не может вытечь из капилляра под действием силы тяжести. Это объясняется проявлением действия капиллярного потенциала, направленного против силы тяжести, так как на нижнем конце капилляра жидкость образует мениск с положительной кривизной. Если часть капилляра, находящаяся над жидкостью, меньше высоты поднятия жидкости, жидкость из него не вытекает, так как кривизна мениска жидкости вверху капилляра становится положительной (положительный радиус кривизны), отвечающей гидростатическому давлению столба жидкости, равному размеру (высоте) капилляра, т. е. устанавливается равновесие. |
ассчитайте время половинной коагуляции аэрозоля с дисперсностью частиц 2,5·108 м-1 и концентрацией 1,5·10-3 кг/м3, если константа быстрой коагуляции Смолуховского равна 3·10-19 м3/с. Плотность частиц аэрозоля примите равной 2200 кг/м3.