Курсовая работа ТОЭ. Кремер Сергей Сергеевич_Курсовая ТОЭ. Электрические цепи переменного синусоидального тока (по
 Скачать 0.99 Mb. Скачать 0.99 Mb.
|
|
О  бразовательная автономная некоммерческая организация бразовательная автономная некоммерческая организациявысшего образования «МОСКОВСКИЙ ОТКРЫТЫЙ ИНСТИТУТ» Факультет «Строительства и техносферной безопасности» Направление подготовки 13.03.02 «Электроэнергетика и электротехника» КУРСОВАЯ РАБОТА По дисциплине:______Теоретические основы электротехники________________ На тему: Электрические цепи переменного синусоидального тока (по вариантам) Обучающийся группы ООБЭЭ-20088 ФИО: Кремер Сергей Сергеевич Москва, 2020 г. СОДЕРЖАНИЕ 1 ЗАДАНИЕ 4 2 ИСХОДНЫЕ ДАННЫЕ ПО ВАРИАНТУ 5 3 СОСТАВЛЕНИЕ СИСТЕМЫ УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА В ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНОМ ВИДЕ ДЛЯ МГНОВЕННЫХ ЗНАЧЕНИЙ ТОКОВ И НАПРЯЖЕНИЙ 7 4 РАСЧЕТ ТОКОВ В ВЕТВЯХ ЦЕПИ МЕТОДОМ УЗЛОВЫХ ПОТЕНЦИАЛОВ 9 5 ОПРЕДЕЛЕНИЕ РЕЖИМОВ РАБОТЫ ИСТОЧНИКОВ. СОСТАВЛЕНИЕ БАЛАНСА МОЩНОСТЕЙ 13 6 РАСЧЕТ ТОКА В ВЕТВИ МЕТОДОМ ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА 15 7 ПОСТРОЕНИЕ ГРАФИКА МГНОВЕННОГО ЗНАЧЕНИЯ ТОКА ВЕТВИ 18 8 ОПРЕДЕЛЕНИЕ ПОКАЗАНИЙ ВАТТМЕТРА 19 9 ПОСТРОЕНИЕ ВЕКТОРНОЙ ДИАГРАММЫ ТОКОВ И НАПРЯЖЕНИЙ 20 СПИСОК ЛИТЕРАТУРЫ 21 1 ЗАДАНИЕДля электрической цепи переменного синусоидального тока, соответствующей индивидуальному заданию, необходимо выполнить следующие расчеты и графические построения: 1) составить систему уравнений по законам Кирхгофа в интегрально-дифференциальном виде для мгновенных значений напряжений и токов; 2) выполнить расчет токов в ветвях электрической цепи методом, указанным в варианте задания, с проверкой правильности расчетов посредством баланса мощностей и оценкой их точности; 3) определить режимы работы источников, имеющихся в заданной электрической цепи; 4) рассчитать ток в указанной ветви или напряжение холостого хода между заданными узлами методом эквивалентного генератора (МЭГ); 5) для заданного тока i(t) или напряжения u(t) построить график мгновенных значений; 6) рассчитать показания ваттметра, включенного в одну из ветвей электрической цепи; 7) построить векторную диаграмму токов и напряжений для ветви, в которой включен ваттметр. 2 ИСХОДНЫЕ ДАННЫЕ ПО ВАРИАНТУПо номеру договора 1066509 определим исходные данные для выполнения курсовой работы. Расчетную схему по варианту №9 представим на рисунке 1. 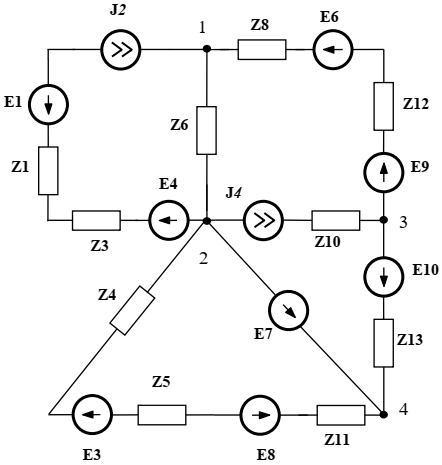 Рисунок 1 – Расчетная схема Числовые значения параметров схемы по варианту №0 представим в таблице 1. Таблица 1 – Исходные данные
Продолжение таблицы 1
Так как сумма двух последних цифр номера договора нечетная (0+9=9), то основной метод расчета электрической цепи – метод узловых потенциалов (МКТ). Так как сумма трех последних цифр номера договора четная (5+0+9=14), то расчет мгновенного значения методом эквивалентного генератора выполним для тока i(t). 3 СОСТАВЛЕНИЕ СИСТЕМЫ УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА В ИНТЕГРАЛЬНО-ДИФФЕРЕНЦИАЛЬНОМ ВИДЕ ДЛЯ МГНОВЕННЫХ ЗНАЧЕНИЙ ТОКОВ И НАПРЯЖЕНИЙИзобразим схему цепи заменив полные сопротивления Z их комплексными составляющими, а также укажем направления токов в ветвях (см. рисунок 2). 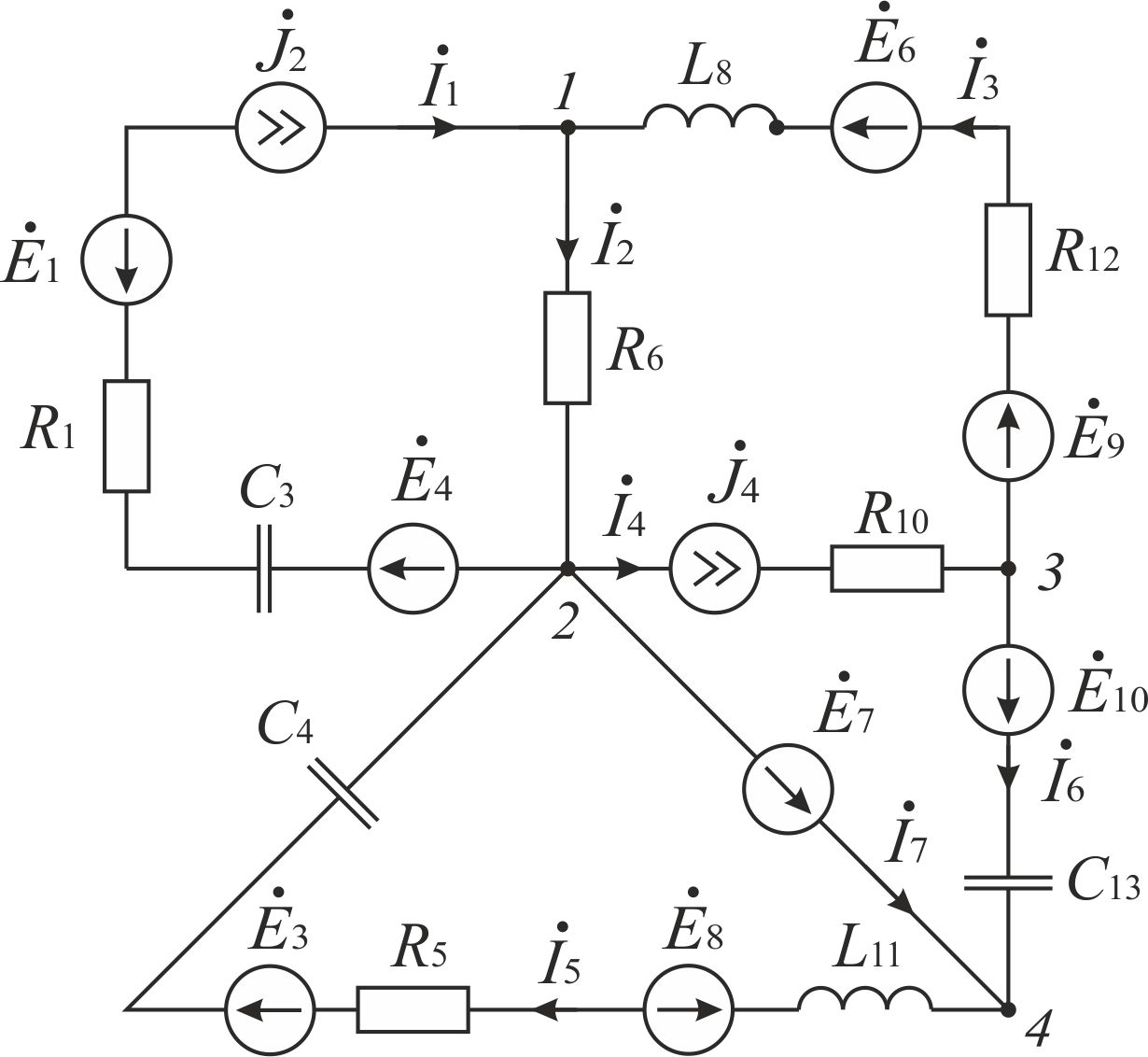 Рисунок 2 – Расчетная схема Для составления уравнений по законам Кирхгофа произвольно выбираем условно - положительные направления токов в ветвях и направления обхода. В рассматриваемой схеме: узлов q = 4, ветвей p = 7, независимых контуров n = p – (q –1) = 7 – (4 – 1) = 4. Следовательно, по первому закону Кирхгофа должно быть составлено (q –1) = 3 уравнения, а по второму закону Кирхгофа n = 4 уравнения. Для мгновенных значений токов, напряжений и ЭДС система уравнений по законам Кирхгофа имеет вид: С учетом того, что: Выражения (1)..(7) запишем в виде: 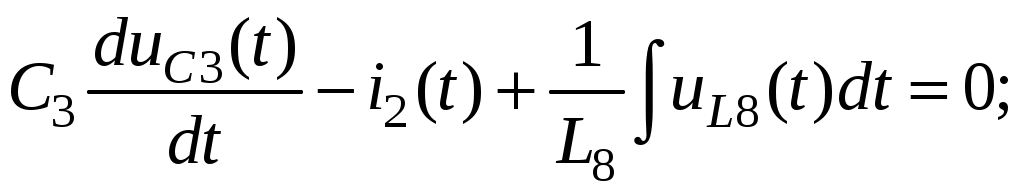 (8) (8)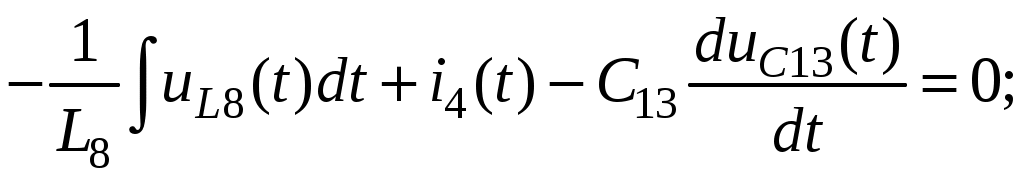 (10) (10)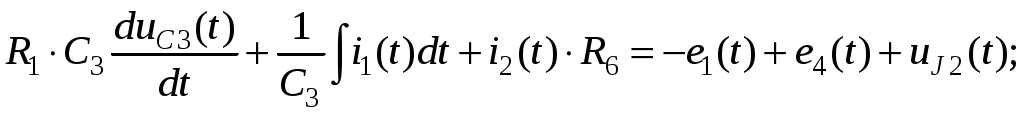 (11) (11)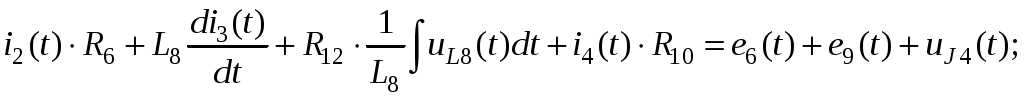 (12) (12)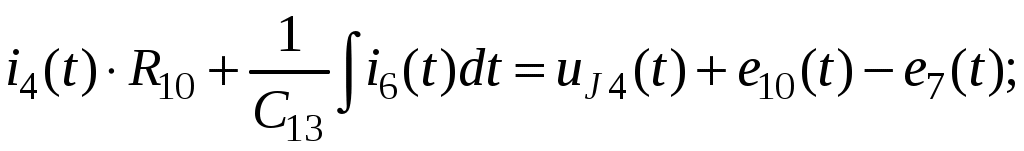 (13) (13)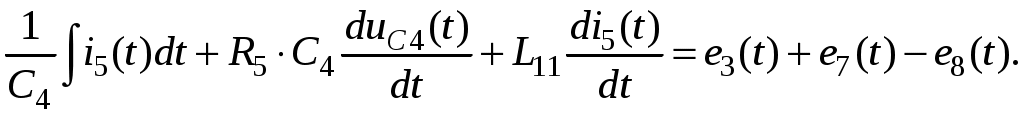 (14) (14)4 РАСЧЕТ ТОКОВ В ВЕТВЯХ ЦЕПИ МЕТОДОМ УЗЛОВЫХ ПОТЕНЦИАЛОВ Запишем комплексы действующих в ветвях ЭДС в символической форме: Запишем комплекс действующего тока источника в символической форме: В соответствии с выбранной нумерацией узлов (рисунок 2), примем 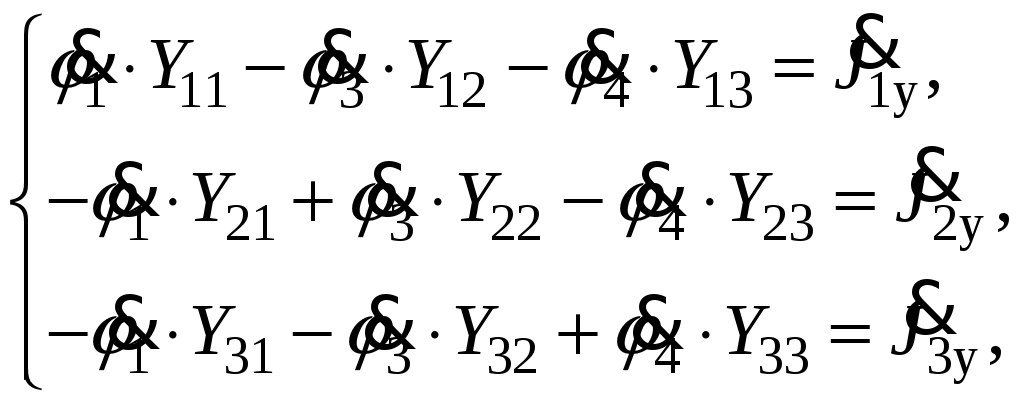 (17) (17)Так как потенциал то систему (17) упрощаем до двух уравнений с двумя неизвестными: 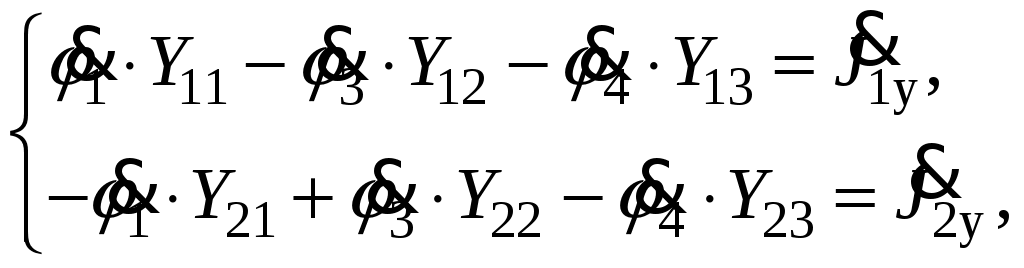 (19) (19)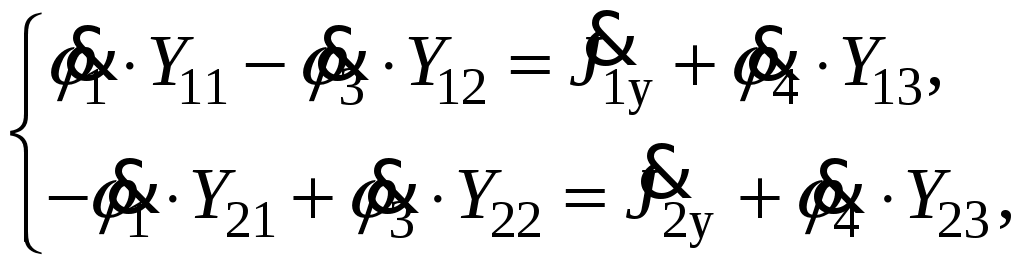 (20) (20)где 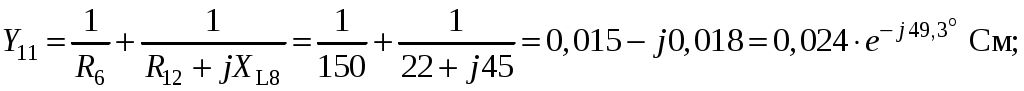 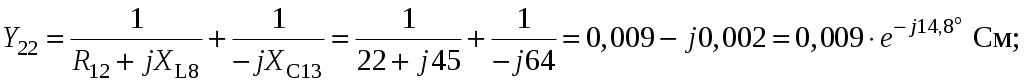 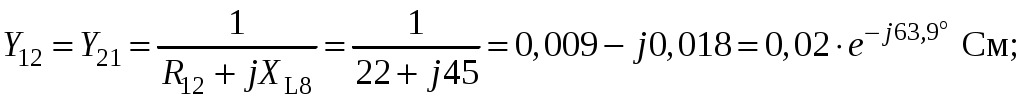 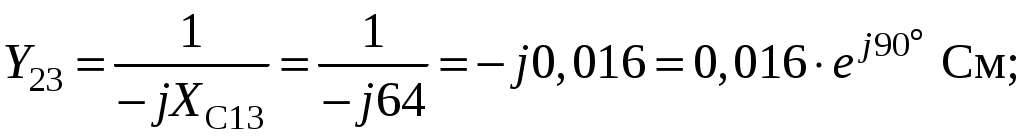 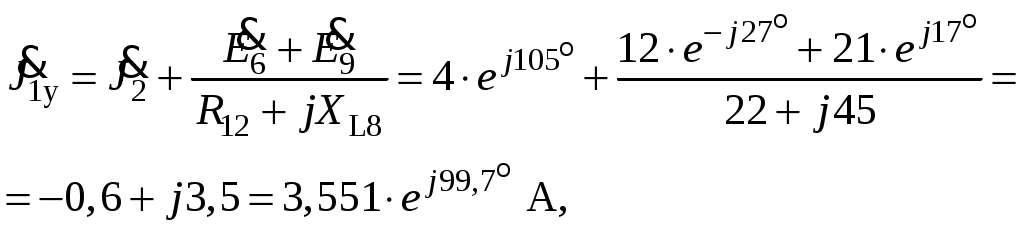 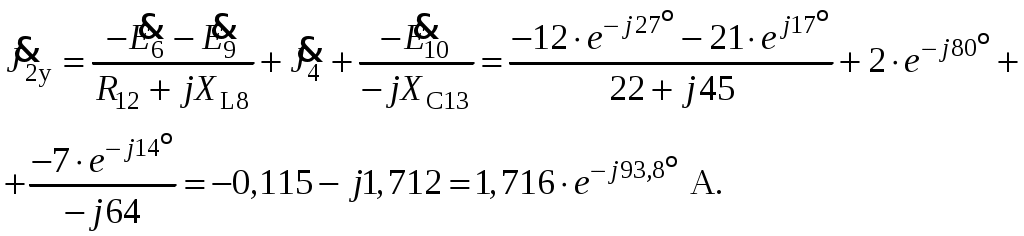 Подставляем известные значения в систему: 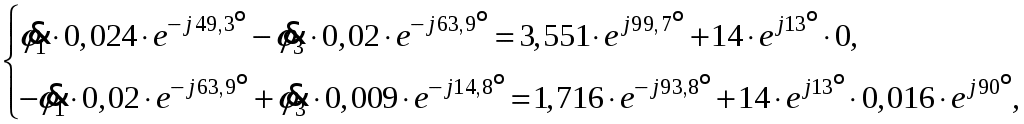 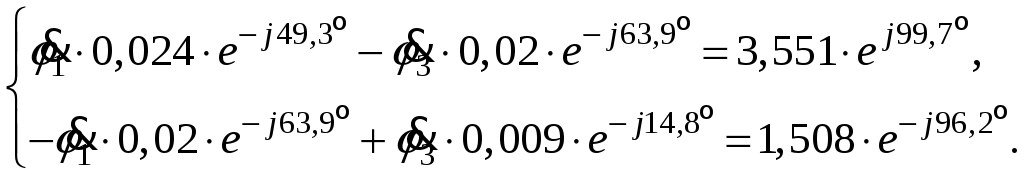 Решение системы относительно неизвестных потенциалов дает: Комплексы действующих токов в ветвях определяем на основании выбранных положительных направлений и по выражению: 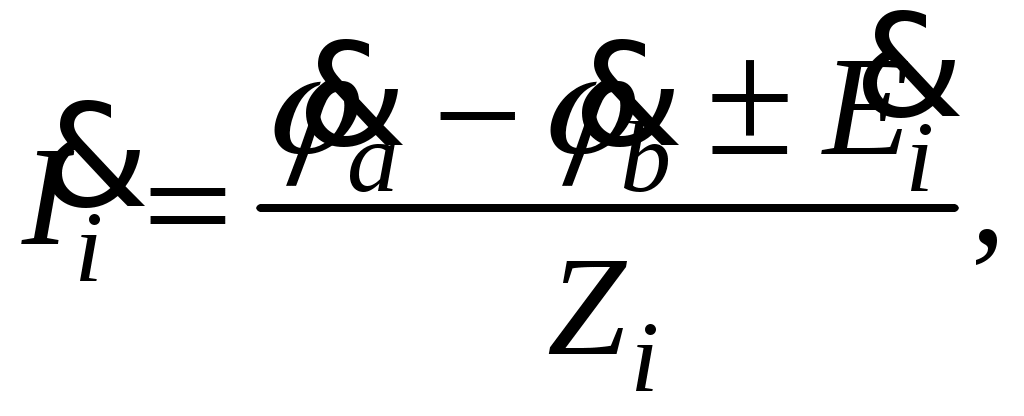 (21) (21)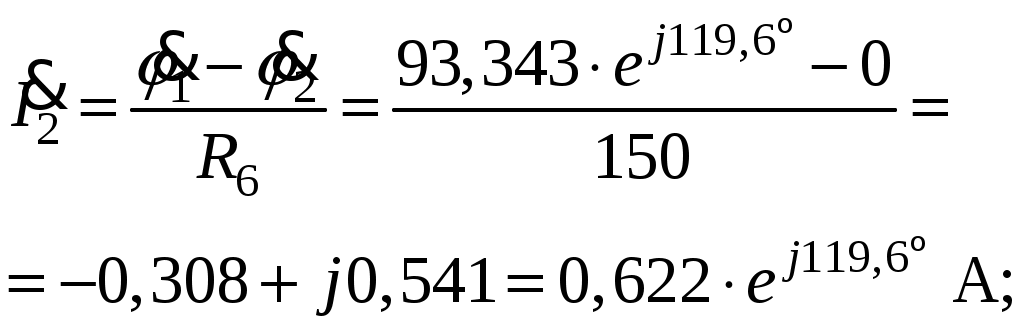 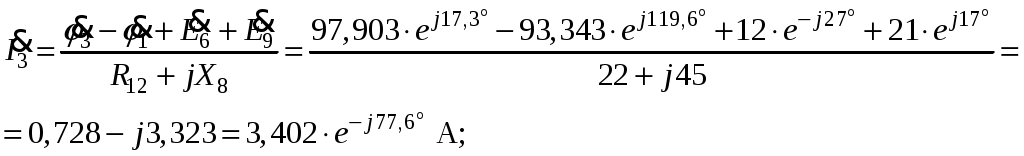 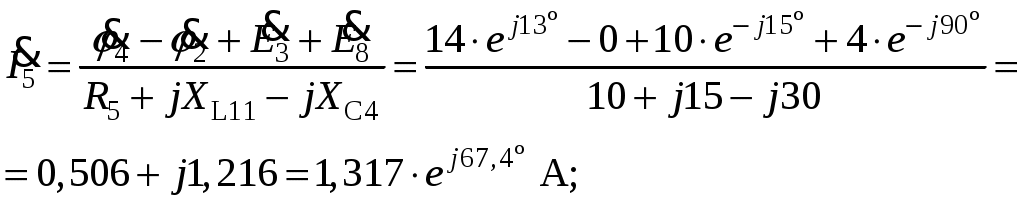 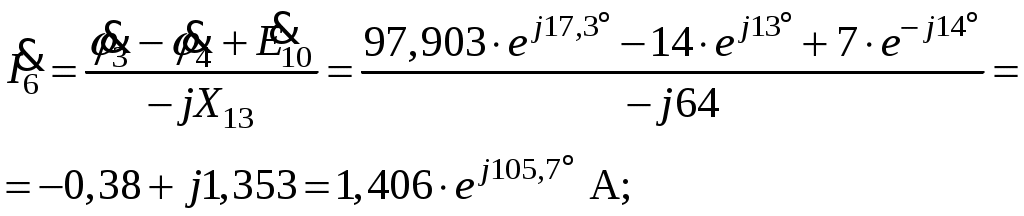 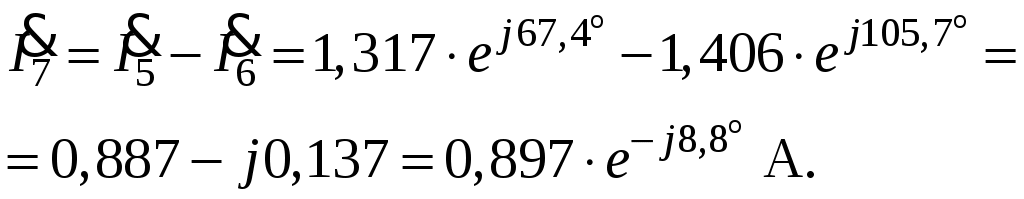 5 ОПРЕДЕЛЕНИЕ РЕЖИМОВ РАБОТЫ ИСТОЧНИКОВ. СОСТАВЛЕНИЕ БАЛАНСА МОЩНОСТЕЙРежимы работы источников схемы (рисунок 2) определяются по комплексам полных мощностей этих источников: Если Р > 0, источник работает в режиме генератора, если Р < 0 – в режиме потребителя. Определим комплексы полных мощностей для источников схемы и определим режим их работы: где 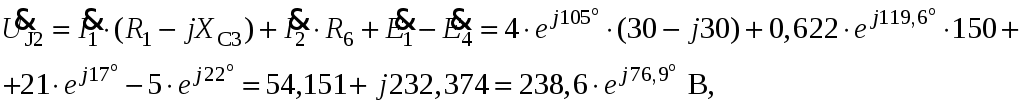 где 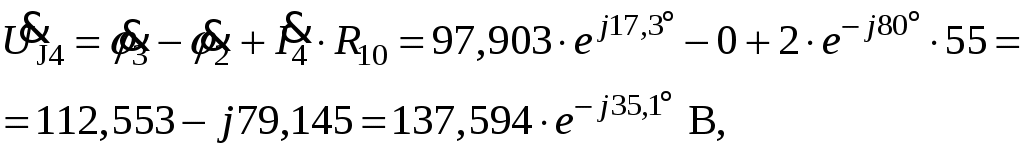 Составим баланс активных и реактивных мощностей. Определим полную мощность источников: 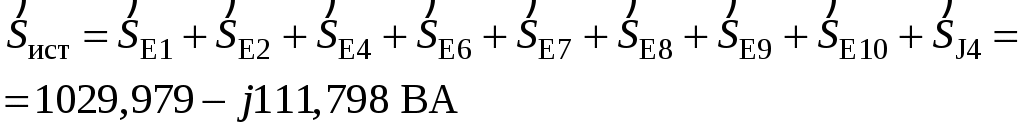 Активная мощность источников: Реактивная мощность источников: Знак «минус» говорит о преобладании емкостной нагрузки в цепи. Определим активную мощность приемников цепи: 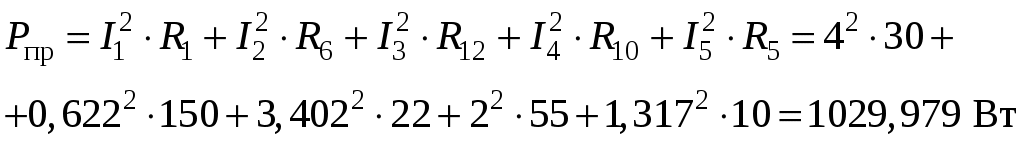 Определим реактивную мощность приемников цепи: 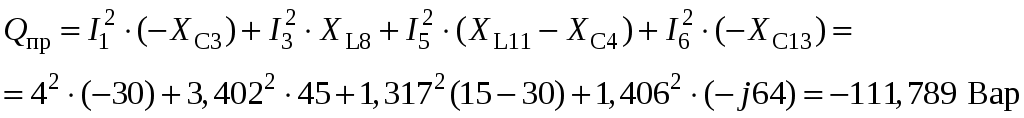 Как видим, баланс мощностей сходится. 6 РАСЧЕТ ТОКА В ВЕТВИ МЕТОДОМ ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРАСогласно варианта задания необходимо рассчитать мгновенное значение тока i(t) через сопротивление Z1 (R1). Участок с заданным сопротивлением исключим из схемы и заменим эквивалентным генератором с напряжением на выводах Uхх и эквивалентным внутренним сопротивлением Zэг. Схему для расчета напряжения Uхх изобразим на рисунке 3. 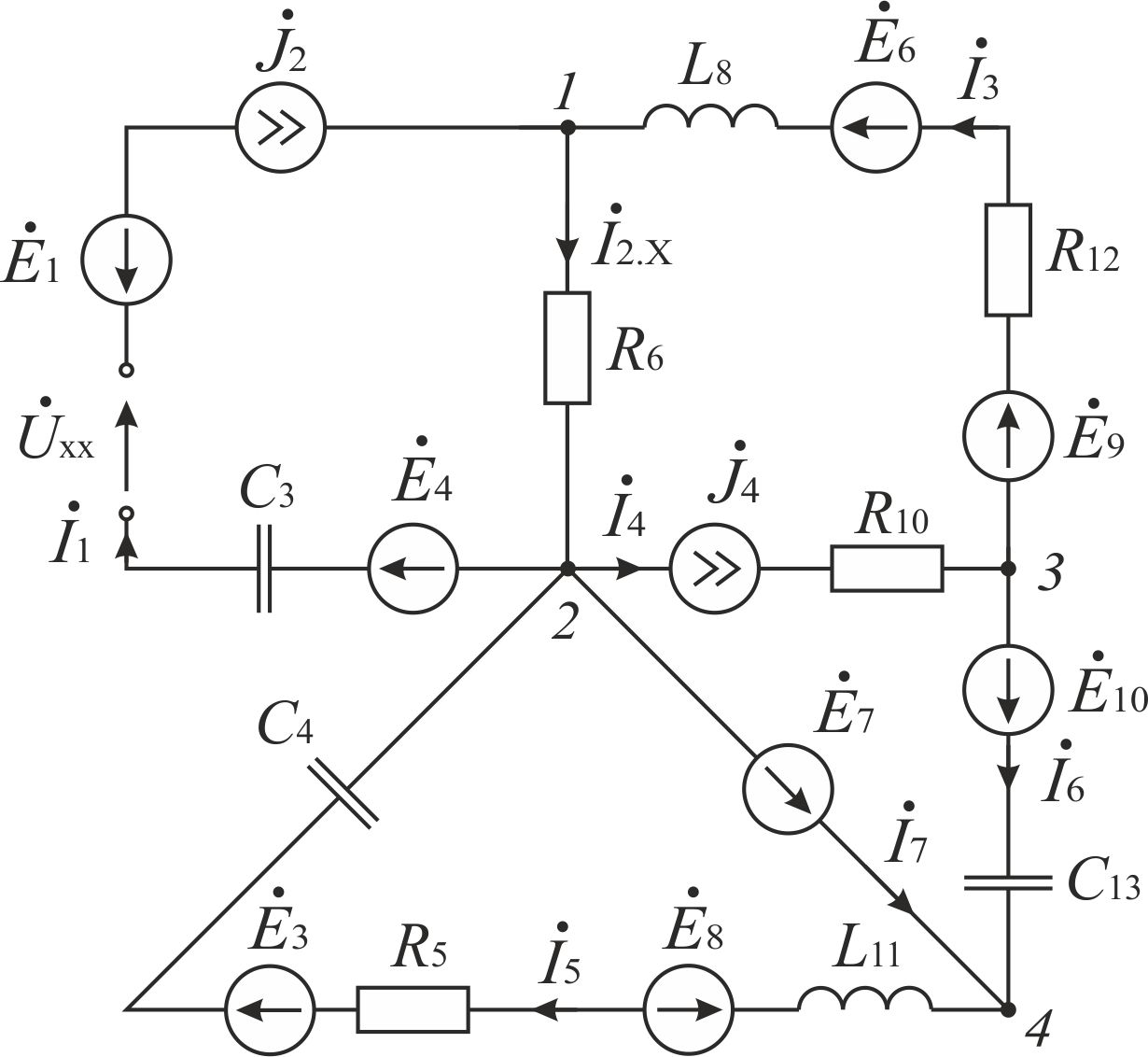 Рисунок 3 – Расчетная схема для метода эквивалентного генератора На основании второго закона Кирхгофа имеем: Определим ток I2.Х по рассмотренному ранее методу узловых потенциалов. Также примем 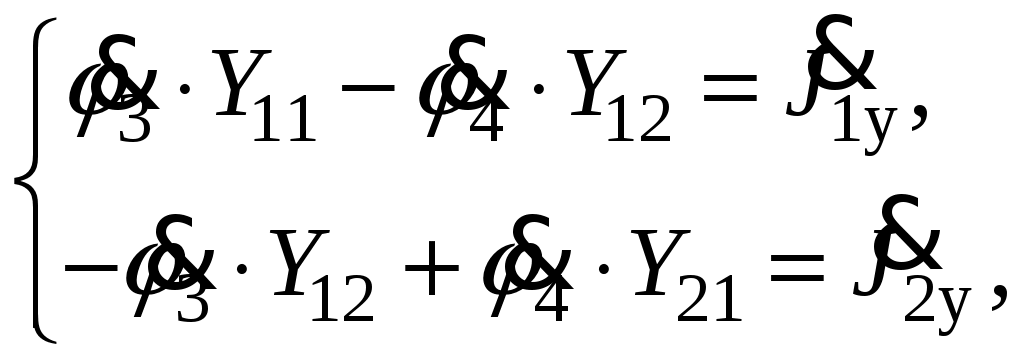 (24) (24)Так как потенциал то систему (24) упрощается до одного уравнения: 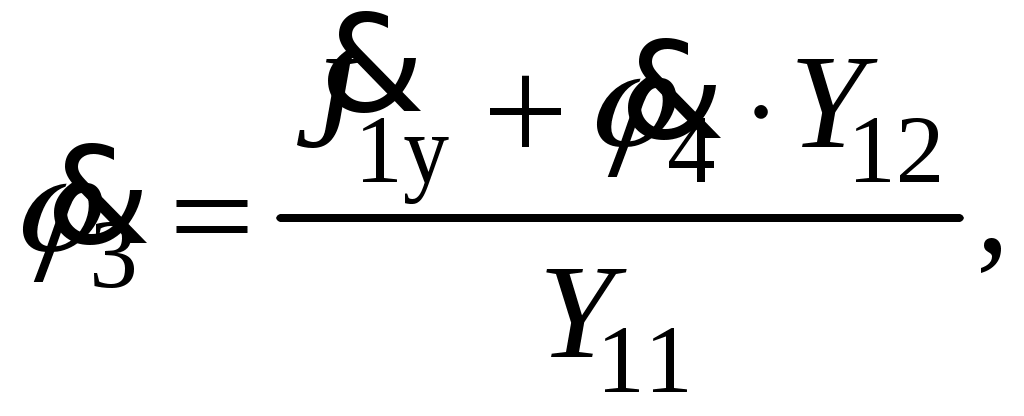 (27) (27)где 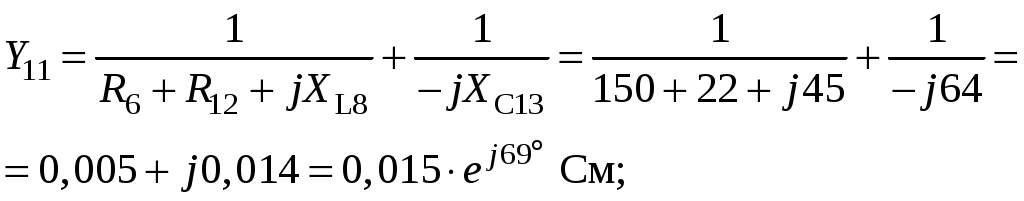 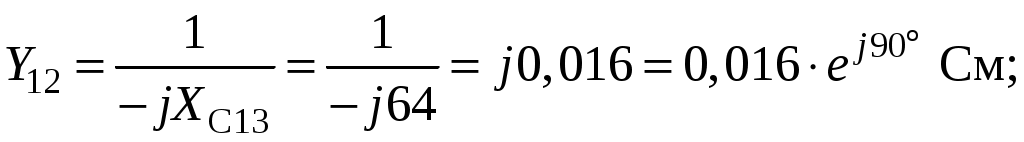 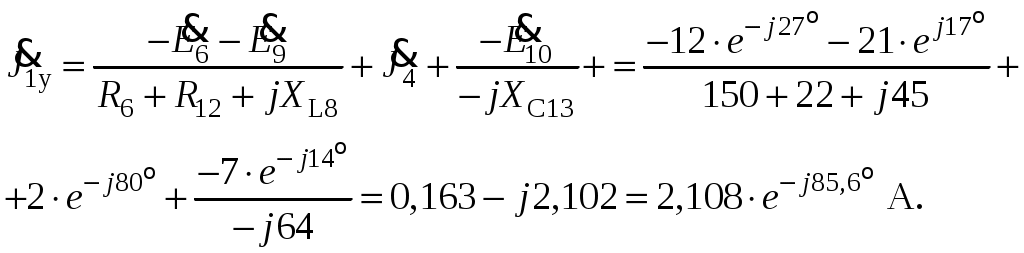 Определяем потенциал точки 3 по (27): 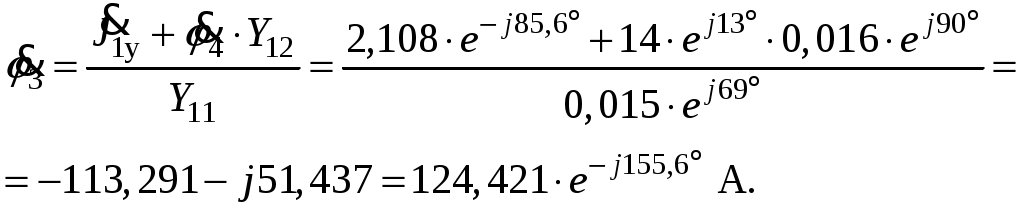 Определяем ток I2.Х по (21): 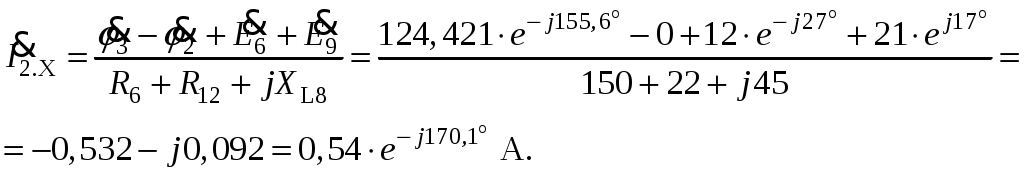 Рассчитываем напряжение холостого хода методом эквивалентного генератора по (23): 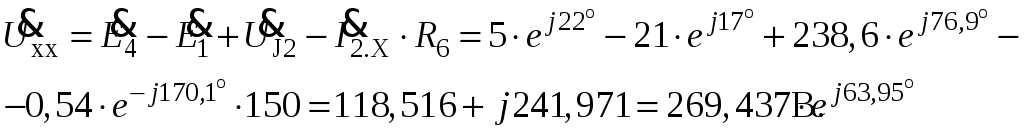 Схема для расчета сопротивления эквивалентного генератора Zэг имеет вид, представленный на рисунке 4. 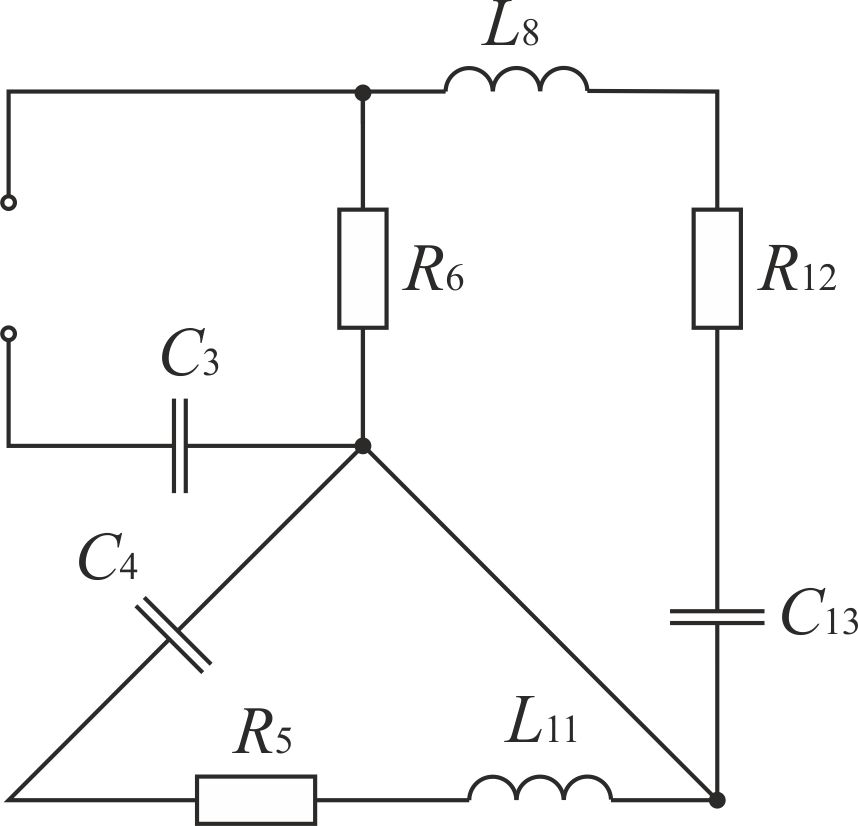 Рисунок 4 – Схема к определению эквивалентного сопротивления Комплекс полного сопротивления эквивалентного генератора определяется выражением: 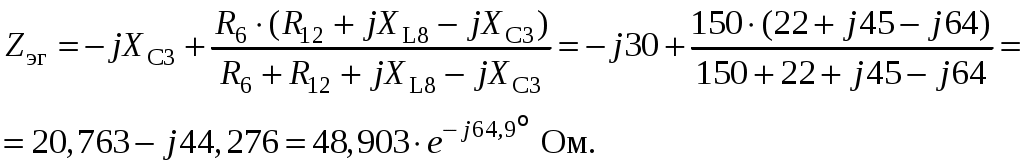 Комплекс тока искомой ветви находим по выражению: 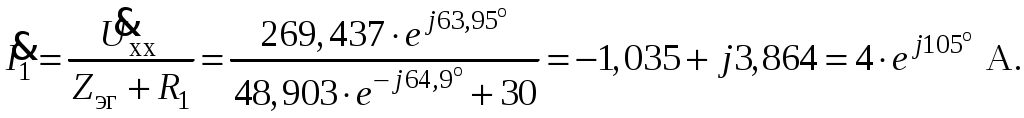 По полученному комплексу тока в ветви получаем амплитудное значение 7 ПОСТРОЕНИЕ ГРАФИКА МГНОВЕННОГО ЗНАЧЕНИЯ ТОКА ВЕТВИДля заданного тока, определенного по методу эквивалентного генератора, построим график мгновенного значения (рисунок 5). 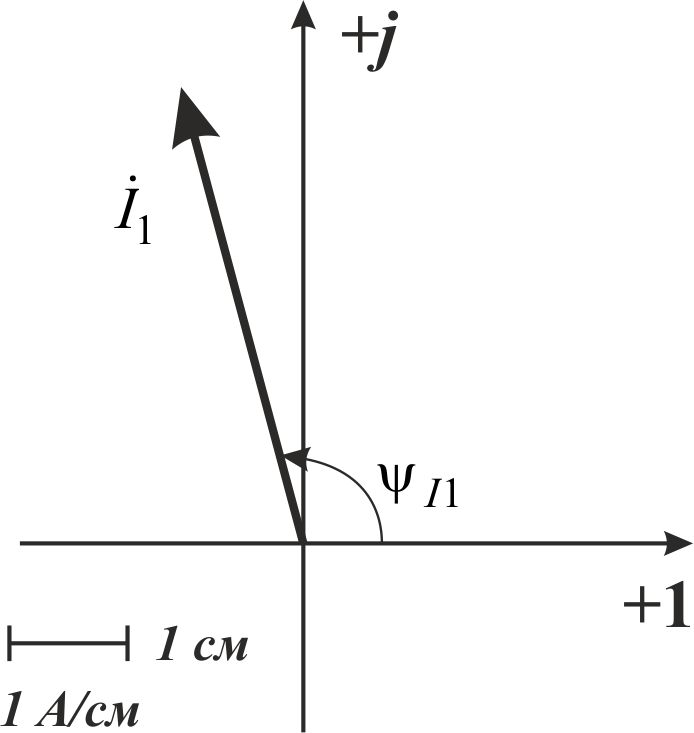 Рисунок 5 – График мгновенного значения тока 8 ОПРЕДЕЛЕНИЕ ПОКАЗАНИЙ ВАТТМЕТРАВ задании указано, что ваттметр должен быть включен между точками 1 и 2. Между этими узлами расположена ветвь с сопротивлением R6. Ваттметр должен быть подключен так, чтобы положительное направление тока ветви совпадало с направлением тока от клеммы I* к клемме I, а положительное направление падения напряжения U12 совпадало с направлением от клеммы U* к клемме U. Подключение ваттметра изобразим на рисунке 6. 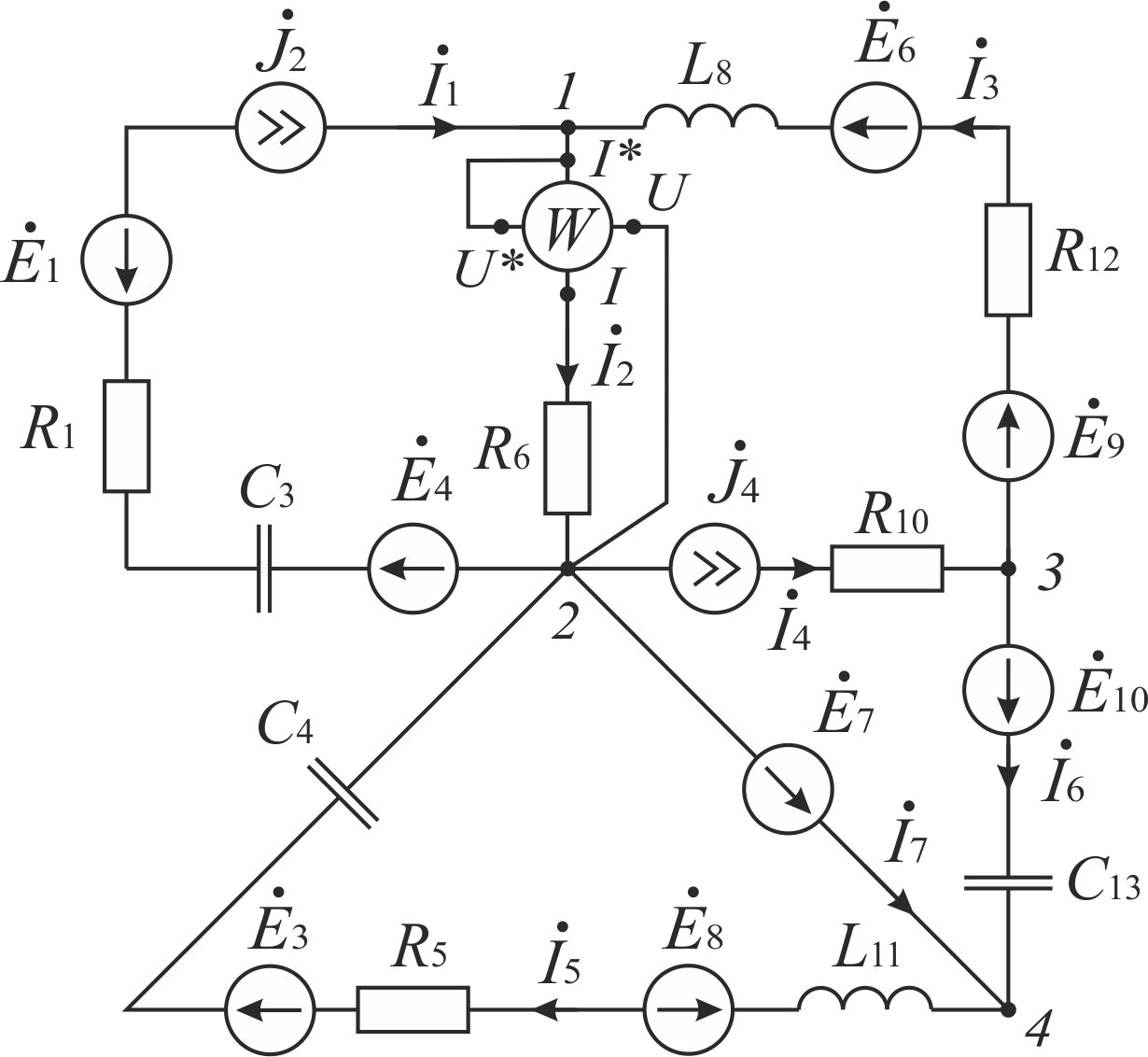 Рисунок 6 – Схема подключения ваттметра Мощность, измеряемая ваттметром, определяется выражением: где U12 – действующее значение напряжения между узлами 1 и 2; I2 – действующее значение тока в выбранной ветви; Действующие значения и начальные фазы А комплекс напряжения Таким образом, показание ваттметра: 9 ПОСТРОЕНИЕ ВЕКТОРНОЙ ДИАГРАММЫ ТОКОВ И НАПРЯЖЕНИЙДля ветви, в которой включен ваттметр, построим векторную диаграмму токов и напряжений (см. рисунок 7). 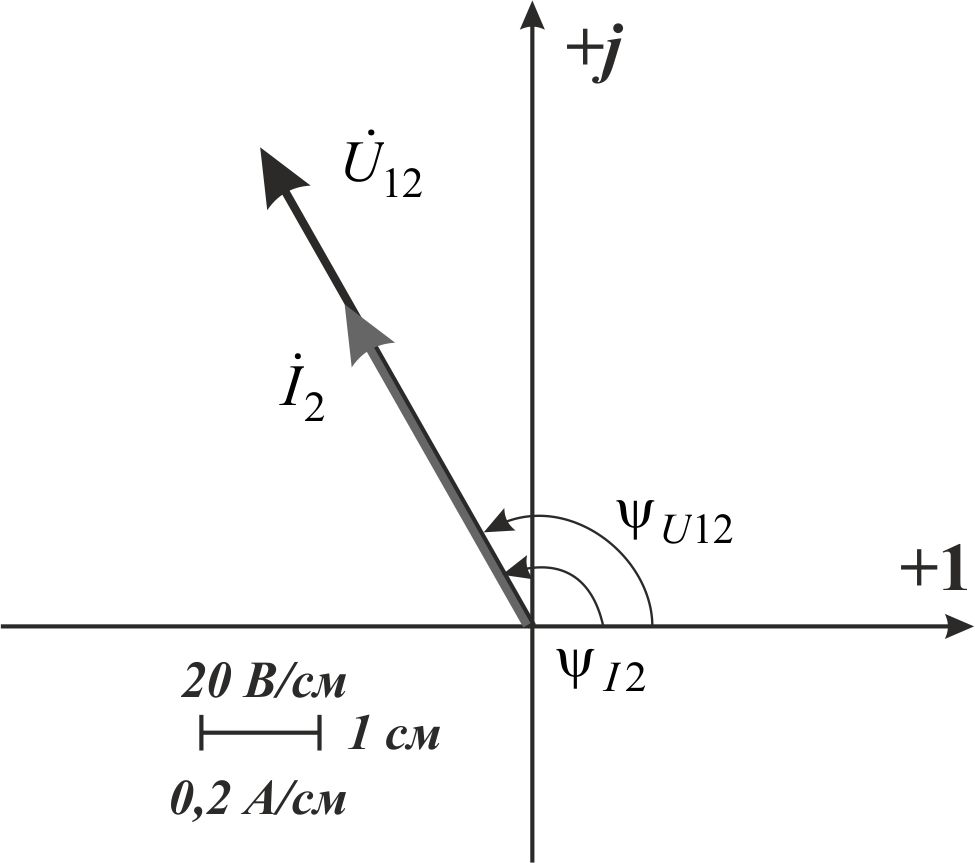 Рисунок 7 – Векторная диаграмма токов и напряжений для ветви с ваттметром СПИСОК ЛИТЕРАТУРЫ1. Демирчян К. С. Теоретические основы электротехники : учебник для вузов : доп. М-вом образования РФ. Т.1 / К. С. Демирчян, Л. Р. Нейман, Н. В. Коровин. – 5-е изд. – Санкт-Петербург : Питер, 2009. – 512 с. 2. Арсеньев Г. Н. Основы теории цепей : учебное пособие : рек.гос. образ. учрежд. / Г. Н. Арсеньев, В. Н. Бондаренко, И. А. Чепурнов; под ред. Г. Н. Арсеньева. – Москва : ИД "ФОРУМ" – ИНФРА-М, 2011. – 448 с. 3. Основы теории цепей. Часть 1 : учебное пособие / П. А. Попов, И. В. Лазарев, С. С. Никулин, С. Л. Анисимов. – Воронеж : Воронежский институт МВД России, 2009. – 153 с. 4. Основы теории цепей. Часть 2 : учебное пособие / П. А. Попов, И. В. Лазарев, С. С. Никулин, С. Л. Анисимов. – Воронеж : Воронежский институт МВД России, 2009. – 127 с. 5. Астайкин А. И. Основы теории цепей : учебное пособие для студентов высших учебных заведений. – Москва : Академия, 2009.− 304 с. 6. Попов В. П. Основы теории цепей: учебник для вузов. 6-е изд., перераб. и доп. – Москва : Высшая школа, 2008. – 575 с. 7. Бакалов В. П. Основы теории цепей: учебник для вузов / В. П. Бакалов, В. Ф. Дмитриков, Б. Е. Крук; под ред. В. П. Бакалова. –Москва : Радио и связь, 2000. – 592 с. 8. Белецкий А. Ф. Теория линейных электрических цепей. – Москва : Радио и связь, 1986. – 544 с. 9. Лосев А. К. Теория линейных электрических цепей. – Москва : Высшая школа, 1987. – 512 с. |
