правила кирхгофа 2. Электрические цепи постоянного тока Задание 1

• Название: Электрические цепи постоянного тока Задание 1
• Дата: 23.11.2020
• Размер: 0.5 Mb.
• Имя файла: правила кирхгофа 2.docx
• Тип: Закон; #153064
• страница: 2 из 5

Пример2.1. Для электрической цепи переменного тока (рис. 2.1) с разомкнутыми переключателями S1и S2 по заданным параметрам потребителей и действующему значению ЭДС (табл. 2.2) выполнить следующее:

1) Изобразить схему замещения, соответствующую разомкнутому положению переключателей S1, S2 и параметрам потребителей;

2) определить ток и напряжения на всех элементах схемы замещения;

3) определить активную, реактивную и полную мощность цепи, показания ваттметра и вольтметра, включенного между точками a и b на схеме.

4) построить топографическую диаграмму напряжений по внешнему контуру.

Таблица 2.2

Е1, В	f, Гц	Z1	Z4
R1, Ом	L1, мГн	С1, мкФ	R4, Ом	L4, мГн	С4, мкФ
120	50	4	57,3	-	2	-	318,5

Решение. Схема замещения приведена на рис. 2.3. Так как переключатели S1, S2 разомкнуты, Z2 и Z3 не подключены и на схеме не изображены. В соответствии с условно-положительным направлением на схеме указаны направление тока I и напряжений на элементах схемы замещения.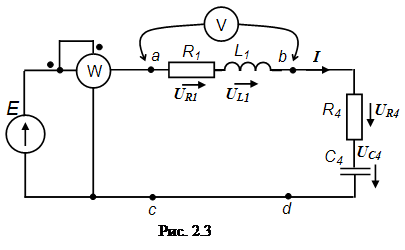



Определяем индуктивное и емкостное сопротивления данной цепи: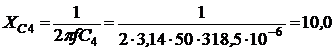

 Ом;

 Ом.

Комплексные сопротивления приемников Z1:

Z₁=R₁ + jX_L1=4 + j18,

и Z₄:

Z₄=R₄ - jX_C4=2 – j10.

Уравнение, составленное по второму закону Кирхгофа в комплексной форме:



или

где Z – комплексное сопротивление цепи,



Комплексное сопротивление цепи записано в алгебраической форме. Здесь действительной составляющей соответствует активное сопротивление цепи, R=R₁+R₄=6 Ом, а мнимой составляющей – реактивное сопротивление X=X_L1-X_C4=8 Ом. Для последующих вычислений целесообразно перейти к показательной форме:



где Z – полное сопротивление цепи (модуль комплексного сопротивления):   Ом;

φ – аргумент комплексного сопротивления цепи, соответствует углу фазового сдвига между ЭДС и током в данном случае:



Находим ток: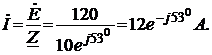



Мощность цепи в комплексной форме определяется, как произведение комплексной ЭДС Ė на сопряженный комплекс тока 

 .

В полученном выражении модуль комплексного числа, S=1440 ВА – полная мощность цепи; действительная часть комплексного числа,   Вт – активная мощность цепи; мнимая часть -   вар – реактивная мощность цепи.

Показания ваттметра соответствуют активной мощности Р=864 Вт.

Показания вольтметра на участке ветви между точками а и b соответствуют действующему значению напряжения, приложенному к приемнику Z₁:

 В.

Показания вольтметра можно определить, пользуясь топографической векторной диаграммой, построенной на комплексной плоскости. Каждой точке схемы на топoграфической диаграмме будет соответствовать точка с определенным значением потенциала. Разность потенциалов любых двух точек укажет на напряжение между этими точками.

Для построения топографической диаграммы (рис. 2.3) примем потенциал точки с равным нулю:   . Потенциал точки d также равен нулю (   ). Тогда потенциал точки b, выраженный через потенциал точки с равен:



Аналогично потенциал точки а:



ЭДС равна сумме напряжений на элементах схемы замещения:



Напряжение на отдельных элементах схемы замещения:

 ;

 ;

 ;



[Примечание:   , т.е. умножение на j соответствует повороту вектора в комплексной плоскости на 90⁰ против часовой стрелки, а умножение на - j соответствует повороту вектора на 90⁰ по часовой стрелки.]



Напряжение между точками а и b указано на векторной диаграмме вектором, проведенной пунктирной линией. Длина вектора соответствует показаниям вольтметра.

Рассмотрим применение символического метода для расчета разветвленных электрических цепей.

Пример2.2. Для электрической цепи переменного тока (рис. 2.5) по заданным параметрам потребителей и действующему значению ЭДС (табл. 2.3) выполнить следующее:

1) определить токи во всех ветвях электрической схемы;

2) составить баланс активной и реактивной мощностей

3) определить показания ваттметра и вольтметра, включенного между точками b и c на схеме.

4) построить на комплексной плоскости векторную диаграмму токов и потенциальную векторную диаграмму напряжений по внешнему контуру.

Таблица 2.3

Е1, В	f, Гц	Z1	Z2	Z3
R1, Ом	L1, мГн	С1, мкФ	R2, Ом	L2, мГн	С2, мкФ	R3, Ом	L3, мГн	С3, мкФ
120	50	4	25,5	-	3	-	796,2	8,0	50,9	318,5

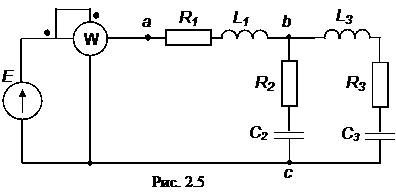Решение. Схема замещения приведена на рис. 2.5. Так как переключатели S1 разомкнут, Z2 и Z3 не подключены и на схеме не изображены. В соответствии с условно-положительным направлением на схеме указаны направление тока I и напряжений на элементах схемы замещения.

Определяем индуктивные и емкостные сопротивления данной схемы: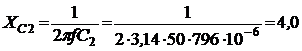

 Ом;

 Ом;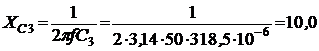

 Ом;

 Ом.

Комплексные сопротивления приемников:

Z₁=R₁ + jX_L1=4 + j8;

Z₂=R₂ – jX_C2=3 – j4;

Z₃=R₃ + j(X_L3–X_C3) =8 + j(16–10)=8+j6.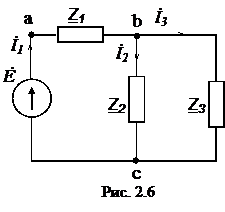

 Схема цепи с комплексными сопротивлениями приведена на рис.2.6.

Расчет такой схемы можно выполнить любым известным методом, но при наличии одного источника ЭДС целесообразно использовать метод эквивалентных преобразований сопротивлений. Заменим параллельные ветви с сопротивлениями одной ветвью с эквивалентным сопротивлением Z_bc. Для удобства расчетов представим Z₂ и Z₃ в показательной форме: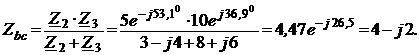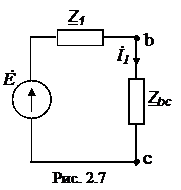

 (     )

 (   )



 Уравнение, составленное по второму закону Кирхгофа в комплексной форме для одноконтурной цепи (рис. 2.7):



или

где Z – комплексное сопротивление цепи,



Находим ток: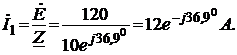



Для определения I₂, I₃ определим напряжение U_bc:



Тогда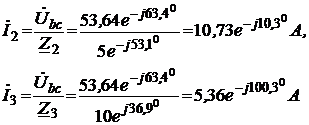



Мощность цепи в комплексной форме определяем, как произведение комплексной ЭДС Ė на сопряженный комплекс тока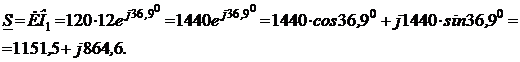 



В полученном выражении модуль комплексного числа – полная мощность цепи:

S=1440 ВА ;

действительная часть комплексного числа – активная мощность цепи:

 Вт ;

мнимая часть – реактивная мощность цепи:

 вар.

Правильность расчетов можно оценить с помощью баланса мощности. Потребители активной мощности имеют в сумме мощность

 Вт.

Потребители реактивной мощности имеют суммарную мощность

 вар

Равенства мощностей (Р=Р_Σ и Q=Q_Σ) с допустимой погрешностью соблюдается.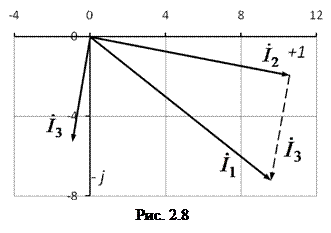

 Показания ваттметра соответствуют активной мощности Р=1152 Вт. Показания вольтметра между точками b и c соответствует ранее определенному напряжению U_bc=53,64 В.

Векторная диаграмма токов на комплексной плоскости приведена на рис.2.8.

Для построения топографической диаграммы (рис. 2.9) примем потенциал точки с равным нулю:   . Тогда потенциал точки b, выраженный через потенциал точки с равен:



Аналогично потенциал точки а:



ЭДС равна сумме напряжений на элементах схемы замещения: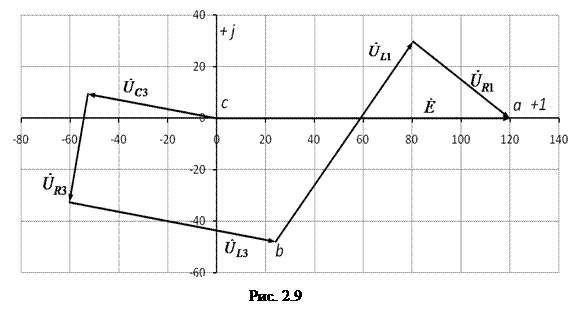





Напряжение на отдельных элементах схемы замещения:

 ;



 ;





[Примечание:   , т.е. умножение на j соответствует повороту вектора в комплексной плоскости на 90⁰ против часовой стрелки, а умножение на - j соответствует повороту вектора на 90⁰ по часовой стрелке.