правила кирхгофа 2. Электрические цепи постоянного тока Задание 1
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Электрические цепи постоянного тока Задание 1 Для заданной электрической схемы по заданным сопротивлениям и ЭДС (табл. 1.1) выполнить следующее: 1) составить систему уравнений, необходимых для определения токов по первому и второму законам Кирхгофа; 2) найти токи во всех ветвях цепи, пользуясь методом контурных токов; 3) проверить правильность расчета токов в ветвях электрической цепи с помощью баланса мощностей; 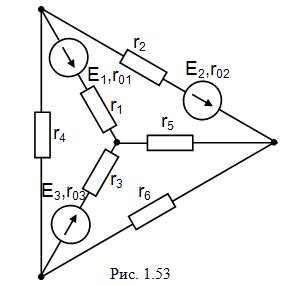
Применение законов Кирхгофа для расчета электрических цепей Для анализа и расчета электрических цепей пользуются законами Кирхгофа, которые устанавливают соотношения между токами ветвей, сходящихся в узлах, и напряжениями элементов, входящих в контуры. Для определения токов и напряжений необходимо составить уравнения цепи с помощью первого и второго законов Кирхгофа. Первый закон Кирхгофа, вытекающий из закона сохранения заряда: алгебраическая сумма токов ветвей, сходящихся в узле электрической цепи, равна нулю: ΣI=0. (1.1) Алгебраическое суммирование осуществляется с учетом направления токов: токи, входящие в узел, считаем положительными, а токи, выходящие из узла - отрицательными. Второй закон Кирхгофа вытекает из закона сохранения энергии: алгебраическая сумма падений напряжений в любом замкнутом контуре равна алгебраической сумме ЭДС в этом контуре: ΣIR=ΣE. (1.2) Суммирование падений напряжений и ЭДС производится с учетом их направлений и выбранного направления обхода контура. Если направление ЭДС и падение напряжения совпадают с направлением обхода контура, то они входят в уравнение (1.2) со знаком плюс, в противном случае – со знаком минус. Метод анализа и расчета электрических цепей на основе первого и второго законов Кирхгофа выполняется в следующем порядке: устанавливается число ветвей и узлов в расчетной цепи; выбираются произвольно условно-положительные направления токов в ветвях и обозначаются на схеме; выбираются произвольно положительные направления обхода контуров для составления уравнений по второму закону Кирхгофа (целесообразно для всех контуров направления обхода выбирать одинаковыми); составляется система из m уравнений по первому и второму законам Кирхгофа, где m - количество неизвестных токов, равное количеству ветвей. По первому закону Кирхгофа можно составить (n-1) независимых уравнений, где n - количество узлов цепи. Остальные [m-(n-1)] уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. контуров, отличающихся хотя бы одной новой ветвью, не вошедшей в предыдущие контуры. Пример 1.1. В качестве примера составим систему уравнений для определения токов в электрической цепи, схема которой изображена на рисунке 1.1,а. Здесь известны сопротивления, величины и направления ЭДС. 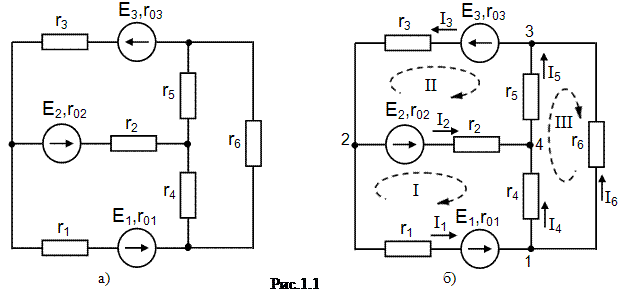 Данная цепь имеет шесть ветвей (m=6) с неизвестными токами и четыре узла (n=4). Необходимо составить шесть уравнений. Выбираем произвольно положительные направления токов в ветвях и положительные направления обхода независимых контуров (по часовой стрелке) (рис, 1.1, б). Чтобы получить линейно независимые уравнения по первому закону Кирхгофа составим три уравнения (n-1=3), а остальные уравнения: m-(n-1)=3, по второму закону Кирхгофа. По первому закону Кирхгофа: - для узла 1 - для узла 2 - для узла 3 . (1.5) По второму закону Кирхгофа: - для контура I: - для контура II: - для контура III:  . (1.8) . (1.8)Полученная система уравнений (1.3 … 1.8) достаточна для определения токов в ветвях цепи, но ее порядок относительно высок. Понизить порядок системы уравнений, а, следовательно, упростить расчеты можно с помощью методов контурных токов и узловых напряжений (потенциалов). Задание 1 1. Составить систему уравнений, необходимых для определения токов по первому и второму законам Кирхгофа (здесь и далее схема развернута); 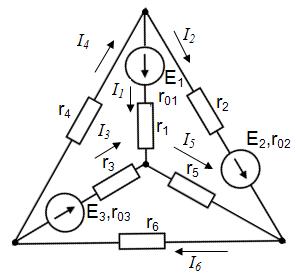 Это самостоятельно! Метод контурных токов этом методе вводят понятие «контурный ток», который протекает по всем ветвям соответствующего независимого контура. Действительные токи ветвей определяются контурными токами. Расчет электрической цепи методом контурных токов выполняют в следующей последовательности: 1. Выбираются произвольно положительные направления контурных токов в независимых контурах и указываются на схеме (целесообразно для всех контуров направления токов выбирать одинаковыми, например, по часовой стрелке); 2. Составляется система уравнений относительно контурных токов на основании второго закона Кирхгофа для каждого независимого контура (направление обхода контура совпадает с направлением контурного тока); 3. Определяются контурные ЭДС (алгебраическая сумма величин ЭДС, входящих в данный контур), собственные сопротивления контуров (сумма сопротивлений ветвей входящих в данный контур), взаимные сопротивления двух смежных контуров (сопротивление ветви входящей одновременно в два рассматриваемых контура); 4. Решается система уравнений относительно контурных токов; определяются действительные токи ветвей по известным контурным токам: токи внутренних (смежных) ветвей схемы определяются как сумма или разность соответствующих контурных токов. Токи внешних ветвей равны соответствующим контурным токам. Метод контурных токов понижает порядок системы уравнений по сравнению с методом непосредственного применения законов Кирхгофа, так как число неизвестных равно числу независимых контуров. 2.Для заданной электрической схемы по заданным сопротивлениям и ЭДС определить токи в ветвях методом контурных токов. Решение. Выбираем произвольно положительные направления контурных токов I11, I22, I33 в независимых контурах. Для электрической цепи с тремя независимыми контурами на основании второго закона Кирхгофа можно записать в формализованном виде эта система уравнений приобретает следующий вид:  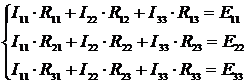 (1.1) (1.1)где: R11, R22, R33 - собственные сопротивления соответствующих контуров: 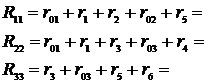 R12, R13, R21, R23, R31, R32 – взаимные сопротивления контуров, т.е. сопротивления смежных ветвей для двух соответствующих контуров, взятые со знаком минус: 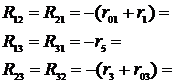 Е11, Е22, Е33 – контурные ЭДС первого, второго и третьего контуров соответственно: 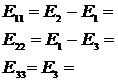 Система уравнений может быть записана непосредственно либо в форме (1.1) либо в матричном виде: 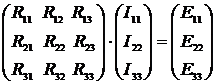 . (1.2) . (1.2)Систему уравнений (1.1) решаем методом Крамера и находим контурные токи: , , , (1.3) где: 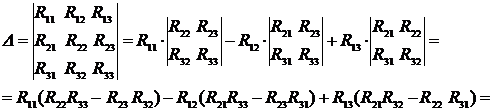 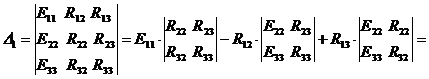 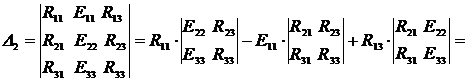 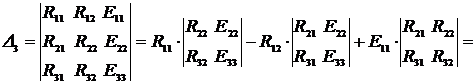 Полученные результаты подставим в (1.3): Если придерживаться направлений токов, принятых для схемы в примере 1, то во внешних ветвях они равны соответствующим контурным токам с учетом направления:  Во внутренних ветвях схемы токи равны разности соответствующих контурных токов: Правильность расчета токов в ветвях электрической цепи можно проверить с помощью уравнения баланса мощности электрической цепи. Из закона сохранения энергии вытекает: в любой электрической цепи сумма мощностей всех источников электрической энергии должна быть равна сумме мощностей всех приемников. Если в электрической цепи имеются только источники ЭДС, то уравнение баланса мощности имеет вид: ΣEI = ΣI2r, (1.19) где ΣEI – алгебраическая сумма мощностей источников ЭДС. Произведение EI входит в сумму со знаком «плюс», если направление тока I, протекающего через источник ЭДС E, совпадает с направлением ЭДС (источник ЭДС отдает энергию в цепь), и со знаком минус, если направления тока I и ЭДС Е не совпадают (источник ЭДС потребляет энергию); ΣI2r - сумма мощностей потребителей резистивного типа, в которых происходит преобразование электрической энергии в тепловую; Если схема имеет не только источники ЭДС, но и источники тока, то при составлении уравнения баланса мощности необходимо учесть их мощность. Общий вид уравнения баланса в этом случае имеет вид: ΣEI+ ΣUJ = ΣI2r, (1.20) где ΣUJ – алгебраическая сумма мощностей источников тока: UJ входит со знаком «плюс», если направления тока J и напряжения U не совпадают, и со знаком «минус», если совпадают. Продемонстрируем проверку результатов расчета токов в ветвях электрической цепи на примере. Задание 1 3) проверить правильность расчета токов в ветвях электрической цепи с помощью баланса мощностей; Проверим с помощью баланса мощностей правильность расчета токов в ветвях электрической цепи Решение. Алгебраическая сумма мощностей источников ЭДС  Сумма мощностей потребителей резистивного типа: Баланс мощностей выполняется. Следовательно, токи в ветвях цепи определены верно. Примечание: При выполнении расчета токов в результате округления чисел возможен небаланс, относительная величина которого δ не должна превышать 0,03: 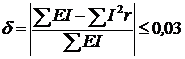 Анализ и расчет электрических цепей синусоидального тока производится с помощью уравнений электрического состояния, составленных с помощью законов Кирхгофа. Первый и второй законы Кирхгофа справедливы для мгновенных значений переменных токов и напряжений. Но тригонометрические преобразования, которые необходимы при анализе разветвленных электрических цепей синусоидального тока, будут очень громоздкими по сравнению с расчетами цепей постоянного тока. Из курса математики и физики известно, что величины, изменяющиеся синусоидально в функции времени, в том числе токи, напряжения и ЭДС, могут быть представлены в виде вращающихся векторов и изображены графически в декартовой системе координат с помощью радиус-векторов. Законы Кирхгофа, записанные в векторной форме, используют для графоаналитического расчета и анализа электрических цепей синусоидального тока. Такие расчеты, выполняемые графически в форме геометрических операций над векторами, просты, наглядны, но не обладают требуемой точностью. Если декартовую систему координат совместить с комплексной плоскостью, то радиус-векторам токов, напряжений и ЭДС будут соответствовать определенные комплексные числа. Это позволяет заменить геометрические операции над векторами алгебраическими операциями над комплексными числами. Законы Ома и Кирхгофа могут быть записаны в комплексной форме. В результате этого, к анализу цепей переменного тока могут быть применены все методы анализа цепей постоянного тока. Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм и высокую точных аналитических расчётов, поэтому рассмотрим этот метод, получивший название символического метода, более подробно. В качестве примера рассмотрим мгновенные значения напряжения u(t), приложенного к приемнику (пассивному двухполюснику), и тока приемника i(t) (рис. 2.2, а). Аналитически они выражаются через синусоидальные функции времени: где Um, Im – амплитуды тока и напряжения, соответственно; ω – угловая частота: ω = 2πf; f – частота переменного тока; ψu , –ψi – начальные фазы напряжения и тока, соответственно. 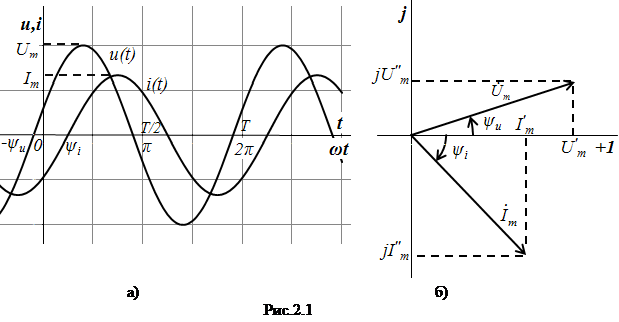 На комплексной плоскости напряжение и ток изображаются радиус-векторами для ωt=0 (рис. 2.2, б). Положение векторов на комплексной плоскости определяется начальной фазой. Так как начальная фаза напряжения больше нуля, то вектор  смещен относительно действительной оси (+1) в положительном направлении (против часовой стрелки) на угол ψu, а вектор тока сдвинут относительно действительной оси на угол -ψi<0 в отрицательном направлении, по часовой стрелке. Радиус-векторам смещен относительно действительной оси (+1) в положительном направлении (против часовой стрелки) на угол ψu, а вектор тока сдвинут относительно действительной оси на угол -ψi<0 в отрицательном направлении, по часовой стрелке. Радиус-векторам представляющие собой координаты точек на концах векторов или проекции векторов на действительную и мнимую оси. Данная форма записи комплексных амплитуд называется алгебраической. Выражая проекции векторов через их длину (модули) и начальную фазу, получим тригонометрическую форму записи комплексных амплитуд:  . (2.4) . (2.4)Из тригонометрической формы комплексного числа вытекает, согласно формулы Эйлера (  (2.5) (2.5)Все три формы записи комплексных амплитуд равнозначны и могут быть использованы при расчетах электрических цепей переменного тока. Выбор формы определяется удобством выполнения требуемой математической операции. На практике при расчетах пользуются действующими значениями. Под комплексом действующих значений синусоидальных токов и напряжений понимают: 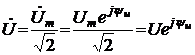 ; (2.6) ; (2.6)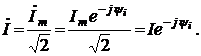 Сопротивление приемника (пассивного двухполюсника), определяемое из закона Ома через комплексы действующих значений напряжения и тока, обозначается Z и называется комплексным сопротивлением: 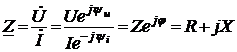 , (2.7) , (2.7)где Z - модуль комплексного сопротивления, ; φ = ψu- (-ψi) = ψu+ ψi – фазовый сдвиг между током и напряжением; R – активное сопротивление приемника: R=Zcosφ; Х – реактивное сопротивление приемника: X=Zsinφ. По первому закону Кирхгофа алгебраическая сумма мгновенных значений токов ветвей, сходящихся в одном узле, равна нулю: . (2.8) В комплексной форме это уравнение запишется как . (2.9) По второму закону Кирхгофа алгебраическая сумма мгновенных значений напряжений любого контура электрической цепи равна нулю: , (2.10) а в комплексной форме (2.11) Если в контуре имеются источники ЭДС, а схемы замещения содержат активные сопротивления R, индуктивные (L) и емкостные(C) элементы, то для замкнутого контура уравнение, составленное по второму закону Кирхгофа, будет иметь в символической форме следующий вид: . (2.12) Мгновенная мощность цепи переменного тока определяется произведением мгновенных значений напряжения и тока Среднее значение мгновенной мощности за период Т называется активной мощностью: 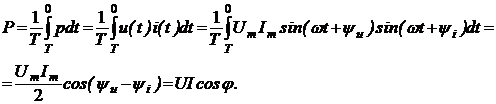 (2.14) (2.14)Активная мощность определяет электрическую энергию, которая необратимо преобразуется в другие виды энергии, в частности, в тепловую: Р=UIcosφ=I2R, Вт. (2.15) В электрической цепи, содержащей индуктивные и емкостные элементы, имеет место непрерывный периодический процесс аккумулирования энергии в этих элементах с последующим разрядом этих элементов. В индуктивном элементе с индуктивностью L энергия аккумулируется в виде магнитного поля: в емкостном элементе с емкостью С в виде электрического поля: Мощность, затрачиваемая на создание этих полей в электрической цепи, определяемая как среднее значение за четверть периода, называется реактивной мощностью Q=UIsinφ=I2X, вар. (2.17) Полная мощность электрической цепи ψI Полная мощность участка цепи в комплексной форме определяется как произведение напряжения на этом участке в комплексной форме на сопряженный комплекс тока Î ( , если ) где φ=ψu – ψi – сдвиг по фазе между током и напряжением. Комплекс полной мощности S в тригонометрической форме состоит из активной мощности Р – действительная часть, и реактивной мощности Q – мнимая часть Для определения мощности источника ЭДС в формулах (2.19) и (2.20) U следует заменить на Е. Рассмотрим применение символического метода на примерах. В качестве примера рассмотрим одноконтурную (неразветвленную) цепь. |
