правила кирхгофа 2. Электрические цепи постоянного тока Задание 1
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
Задание 2 Для электрической цепи переменного тока (рис. 1) с заданным положением переключателей (S1 – разомкнут, S2 – замкнут) по заданным параметрам потребителей Z1, Z3, Z4, и действующему значению ЭДС (табл. 2.1) выполнить следующее: 1) Изобразить схему замещения, соответствующую заданным положениям переключателей S1, S2 и параметрам потребителей; 2) определить токи во всех ветвях цепи; 3) составить баланс активной и реактивной мощностей; 4) определить показания ваттметра и вольтметра, включенного между двумя узлами (по заданию преподавателя между узлами b и с); 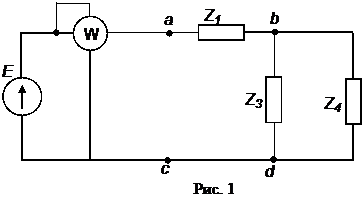
Решение. Схема замещения приведена на рис. 2.2. Так как переключатель S1 разомкнут, Z2 не подключено и на схеме не изображено. В соответствии с условно-положительным направлением на схеме указаны направление токов. 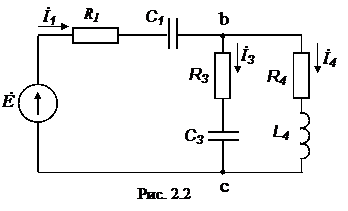 Определяем индуктивные и емкостные сопротивления данной схемы: 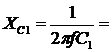 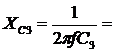 Комплексные сопротивления приемников: Z1=R1 – jXС1= Z3=R3 – jXС3= Z4=R4 +jXL4 = 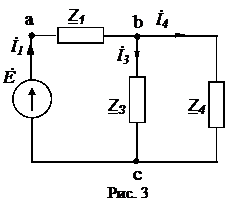 Схема цепи с комплексными сопротивлениями приведена на рис.3. Схема цепи с комплексными сопротивлениями приведена на рис.3.Расчет такой схемы можно выполнить любым известным методом, но при наличии одного источника ЭДС целесообразно использовать метод эквивалентных преобразований сопротивлений. Для удобства расчетов представим Z3и Z4 в показательной форме: где 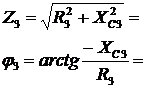 где 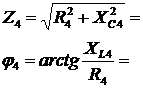 Заменим параллельные ветви с сопротивлениями Z3 и Z4 одной ветвью с эквивалентным сопротивлением Zbc. 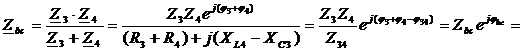 где 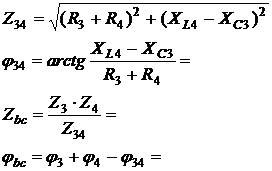 Для последующих расчетов Zbc представим в алгебраической форме где Rbc = Zbc·cosφbc= Xbc = Zbc·sinφbc= 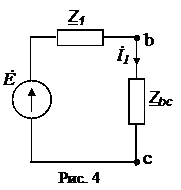 Уравнение, составленное по второму закону Кирхгофа в комплексной форме для одноконтурной цепи (рис. 4): Уравнение, составленное по второму закону Кирхгофа в комплексной форме для одноконтурной цепи (рис. 4):или где Z – комплексное сопротивление цепи,  Находим ток: 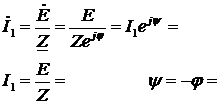 Для определения I3 и I4определим напряжение Ubc:  Тогда  Мощность цепи в комплексной форме определяем, как произведение комплексной ЭДС Ė на сопряженный комплекс тока В полученном выражении модуль комплексного числа – полная мощность цепи: действительная часть комплексного числа – активная мощность цепи: мнимая часть – реактивная мощность цепи: Правильность расчетов можно оценить с помощью баланса мощности. Потребители активной мощности имеют в сумме мощность Потребители реактивной мощности имеют суммарную мощность Равенства мощностей (Р=РΣ и Q=QΣ) с допустимой погрешностью должно соблюдаться. Показания ваттметра соответствуют активной мощности Р. Показания вольтметра между точками b и c соответствует ранее определенному напряжению Ubc. Расчет трехфазных цепей Трехфазная цепь – это совокупность трехфазной системы синусоидальных ЭДС, трехфазной нагрузки и соединительных проводов. Трехфазная система синусоидальных ЭДС: ЕА, ЕВ, ЕС, создаваемая трехфазным генератором, имеет одинаковую амплитуду и частоту. Эти ЭДС сдвинуты по фазе относительно друг друга на 1200. Порядок чередования ЭДС (фаз) таков: если ЕА имеет начальную фазу равную 0, то ЕВ отстает от нее на 1200, а ЕС еще на 1200 (или опережает ЕА на 1200). Обмотки генераторов соединяют либо по схеме «звезда» либо по схеме «треугольник». Аналогично соединяют обмотки трехфазных трансформаторов и трехфазные потребители (приемники). Соединение звездой При соединении обмоток трехфазных генераторов звездой концы фазных обмоток, являющихся источниками трехфазных ЭДС, соединяют в нейтральную точку N. Аналогично в нейтральную точку n соединяют концы фаз приемников Za, Zb, Zc (рис. 3.1). начала фаз обмоток генератора А,В,С и, соответствующие им, начала фаз приемников а,b,с соединяют проводами, которые называют линейными. Провод, соединяющий нейтральные точки генератора N и приемников n, называют нейтральным проводом. Напряжения  , , между началом и концом каждой фазы генератора, и напряжения , , между началом и концом фаз приемника называют фазными напряжениями. , , между началом и концом каждой фазы генератора, и напряжения , , между началом и концом фаз приемника называют фазными напряжениями.Если пренебречь сопротивлениями линейных и нейтрального проводов, то ; ; . Напряжения между линейными проводами , , называют линейными напряжениями. Комплексные действующие значения линейных и фазных напряжений связаны между собой следующими уравнениями:  . (3.1) . (3.1)Векторы фазных напряжений, равны по модулю UA=UB=UC=UФ и сдвинуты по фазе относительно друг друга на угол 1200 (2π/3 рад): ; Здесь приведена показательная форма записи комплексных фазных напряжений. В соответствии (3.1) и (3.2) на рис 3.2 приведена векторная диаграмма фазных и линейных напряжений на комплексной плоскости .  Из диаграммы и из уравнений (3.1) и (3.2) следует, что Из диаграммы и из уравнений (3.1) и (3.2) следует, чтогде UЛ – действующее значение линейного напряжения, . (3.4) Таким образом, четырехпроводная линия позволяет получить две системы: трехфазных напряжений: UФ и UЛ. При известном линейном напряжении сети UЛ и известных сопротивлениях потребителей (Za, Zb, Zc) токи в каждой фазе приемника (фазные токи) в комплексной форме определяются по формулам: 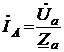 ; ; 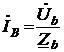 ; , (3.5) ; , (3.5)где 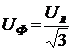 . (3.6) . (3.6)Из схемы (рис 3.1) видно, что при соединении приемников звездой токи линейных проводов , , равны соответствующим фазным токам приемника. В общем виде: . (3.7) Ток в нейтральном проводе: При симметричной нагрузке (Za=Zв=Zc) фазные токи равны по модулю (IA=IB=IC=IФ) , углы сдвига фаз токов по отношению к соответствующим фазным напряжениям одинаковы (φА= φВ= φС= φ), а ток в нейтральном проводе равен нулю: В этом случае нейтраль может отсутствовать. Если нейтраль будет отсутствовать при несимметричной нагрузке (например, в результате обрыва), то это приведет к возникновению разности потенциалов UN между нейтралью источника N и нейтральной точкой потребителя n: 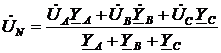 , (3.10) , (3.10)где YA=1/Za; YB=1/Zb; YC=1/Zc. (3.11) В результате фазные напряжения потребителей 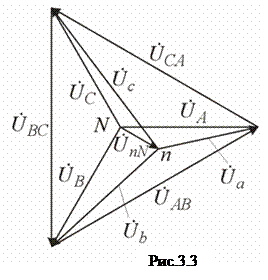 На рис. 3.3 приведена топографическая векторная диаграмма, соответствующая (3.12). Из диаграммы видно, что фазные напряжения потребителей при отсутствии нейтрали заметно отличаются друг от друга, причем напряжение некоторых фаз может существенно превысить номинальное (на диаграмме Uc). Это может привести к выходу из строя оборудования. На рис. 3.3 приведена топографическая векторная диаграмма, соответствующая (3.12). Из диаграммы видно, что фазные напряжения потребителей при отсутствии нейтрали заметно отличаются друг от друга, причем напряжение некоторых фаз может существенно превысить номинальное (на диаграмме Uc). Это может привести к выходу из строя оборудования.Активная и реактивная мощности каждой фазы определяется по формулам: PФ = UФIФcosφ; QФ = UФIФsinφ, (3.1) где – сдвиг по фазе между фазным током и соответствующим фазным напряжением потребителя . Активная мощность трехфазной цепи равна сумме активных мощностей отдельных фаз потребителей: P = Pа + Pb+ Pc; (3.14) Реактивная мощность соответственно: Полная мощность цепи: При симметричной нагрузке: P = 3PФ = 3UФIФcosφ; Q = 3QФ = 3UФIФsinφ. (3. Так как при соединении звездой Активные и реактивные фазные мощности можно определить в комплексной форме пользуясь формулами (2.19), (2.20). ли три фазы приемника с фазными сопротивлениями ZАВ, ZВС, ZСА включить между линейными проводами, как показано на рис. 3.4,то получится соединение фаз приемника треугольником. 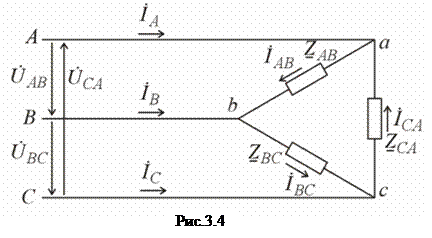 Характерной особенностью такого соединения является равенство фазных напряжений приемника, соответствующим линейным напряжениям линии электропередачи (сети): UФ=UЛ (3.18) Если не учитывать сопротивление проводов сети, то можно считать, напряжение приемника равно линейному напряжению источника. Фазные токи IAВ, IBС, ICА определяются линейными напряжениями сети и фазными сопротивлениями: 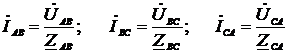 (3.19) (3.19)Линейные токи можно определить через фазные, применяя первый закон Кирхгофа в комплексной форме к узловым точкам а, в, с:  На рис. 3.5 приведена векторная диаграмма токов, исходя из ранее построенной векторной диаграммы напряжений (рис. 3.2). На рис. 3.5 приведена векторная диаграмма токов, исходя из ранее построенной векторной диаграммы напряжений (рис. 3.2).Зная, что вектора линейных напряжений сдвинуты относительно друг друга по фазе на 1200, и, используя соотношения (3.20), можно построить векторные диаграммы токов и напряжений, как это показано ниже (пример 8 рис. 3.11). При симметричной нагрузке Из векторной диаграммы следует, что при симметричной нагрузке линейный и фазный токи связаны отношениями: (3.21) Активная мощность трехфазного приемника равна сумма мощностей отдельных фаз: При симметричной нагрузке: Учитывая, что при симметричной нагрузке можно выразить мощность через линейные токи и напряжения: Аналогично, можно вывести формулы для реактивной мощности Q : Полная мощность в общем случае равна: Для симметричной нагрузки: |
