КОНТРОЛЬНАЯ РАБОТА. Электрической
 Скачать 184.57 Kb. Скачать 184.57 Kb.
|
|
КОНТРОЛЬНАЯ РАБОТА Составить схему замещения электрической системы. Выбрать положительные направления токов ветвей. Определить параметры схемы замещения. Построить направленный граф сети. Выделить в нем дерево и хорды. Проверить правильность выделения дерева и хорд. Пронумеровать узлы и ветви в установленном порядке (базисный узел имеет последний номер). Составить первую и вторую матрицы соединений. Нагрузки представить в виде задающих токов. Составить вектор задающих токов в узлах. 6 Составить матрицу сопротивлений ветвей. Выполнить расчет установившегося режима электрической схемы указанным в задании методом. Полученные в результате расчета токи ветвей и напряжения узлов нанести на граф сети. Уточнить направления ветвей по результатам расчета. Нагрузки представить в виде мощностей. На основании полученных токов в ветвях и напряжений в узлах получить мощности начала и конца ветви и соответственно потери мощности в сети. Проанализировать уровни напряжения на участках сети и уточнить фактические напряжения в узлах нагрузки с учетом коэффициента трансформации. Нанести на граф сети мощности начала и конца ветви, а также напряжения узлов. Проанализировать полученные результаты. Исходные данные Вариант 12 № схемы 4 Номинальное напряжение сети ВН 35 кВ Номинальное напряжение сети НН 10 кВ Метод на основе обобщенного уравнения состояния 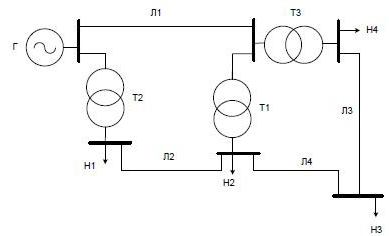 Рисунок 1 – Схема системы №4 Данные линий
Данные трансформаторов
Нагрузки
Решение Заменяем исходную схему схемой замещения, которая представляет собой совокупность схем замещения отдельных элементов. Сопротивления Л1, Л2, Л3, Л4, Т1, Т2, Т3, входящие в схему замещения при расчетах считаем постоянным, при этом схема замещения сети будет представлять собой линейную электрическую цепь. 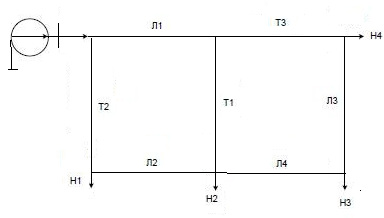 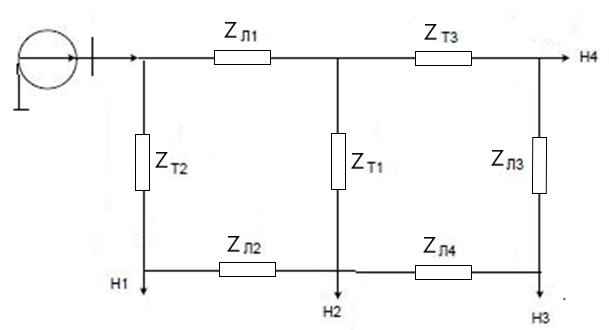 Количество узлов в схеме замещения у нас получилось 6. Обозначим их цифрами в кружочках. Принимаем за нулевой (балансирующий) тот узел, к которому подключен источник питания. Нумеруем узлы и ветви в установленном порядке (базисный узел имеет последний номер). 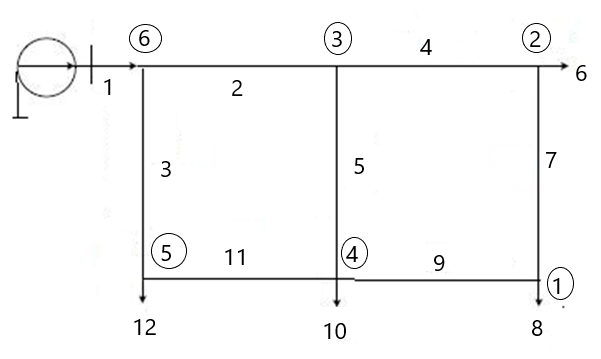 На схеме замещения выбираем положительное направление токов ветвей. 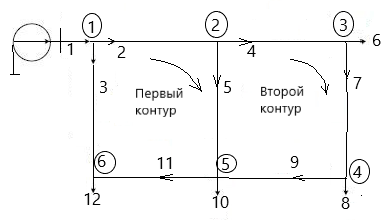 Определяем параметры схемы замещения. Воспользуемся справочными данными линий и трансформаторов. 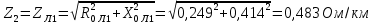 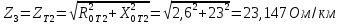 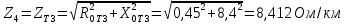 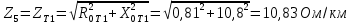 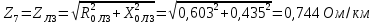 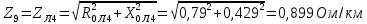 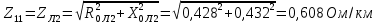 Состояние линейной электрической цепи описываются уравнениями на основе законов Кирхгофа и закона Ома. Согласно первому закону Кирхгофа, который определяет баланс токов в каждом узле электрической цепи, алгебраическая сумма токов в узле равна нулю. Для любого произвольного узла можно записать первый закон Кирхгофа так: 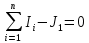 Запишем согласно первого закона Кирхгофа для каждого узла: Для узла 6: 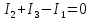 Для узла 5: 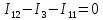 Для узла 4: 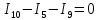 Для узла 3: 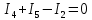 Для узла 2: 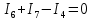 Для узла 1: 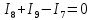 Второй закон Кирхгофа определяет баланс напряжений в контурах электрической цепи, алгебраическая сумма падений напряжений на ветвях контура равна 0. Применим к нашей схеме замещения второй закон Кинхгофа. Для первого контура: 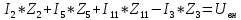 Для второго контура: 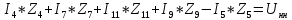 Построение графа сети. Дерево выделено жирной линией, хорды прерывистой линией. Проверить правильность выделения дерева и хорд. Пронумеруем узлы и ветви в установленном порядке (базисный узел имеет последний номер). 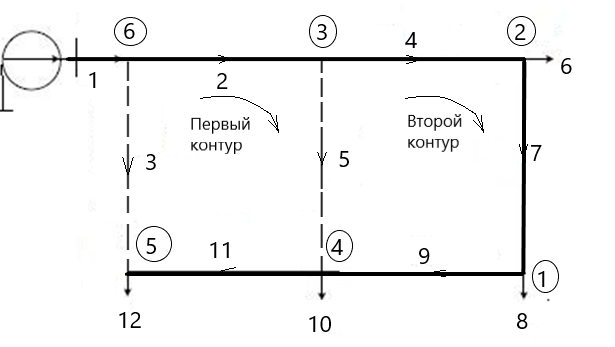 Проверяем правильность выделения дерева и хорд. Число ветвей, входящих в состав дерева на единицу меньше числа узлов всех схемы. Число ветвей 5 (номера ветвей 2,4,7,9 и 11), число узлов 6, итого 6-5=1. Условие выполняется. Число хорд равно числу независимых контуров схемы. У нас два контура, две хорды (пунктирными линиями на схеме хорды 3 и 5). Составляем первую и вторую матрицы соединений. Первая матрица соединений – это матрица соединений ветвей в узлах, число строк которой равно числу вершин графа, а число столбцов равно числу ребер. Номера строк соответствуют номерам вершин (узлов n), номера столбцов – номерам ребер (ветвей m). 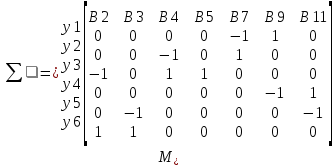 Столбцы матрицы М показывают, с какими узлами соединяется ветвь и кокой из них является началом, а какой концом ветви. Строки показывают, какие ветви присоединяются к данному узлу – началом и концом. Вторая матрица соединений – матрица соединений ветвей в независимые контуры, число строк которой равно числу независимых контуров k, а число столбцов равно числу ветвей m. 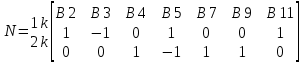 Матрицу N можно разделить на матрицу дерева 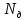 и матрицу хорд и матрицу хорд 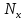 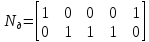 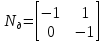 Матрица задающих токов: 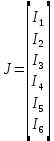 Матрица сопротивлений ветвей: 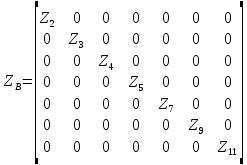 Расчет установившегося режима электрической схемы. Обобщенное уравнение состояния. 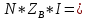 = 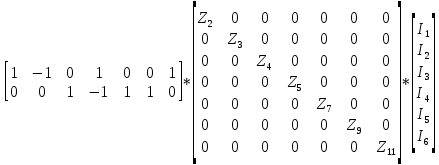 Получаем матричную форму записи второго закона Кирхгофа. Используя матричную форму записи первого и второго законов Кирхгофа, мы получили обобщенное уравнение состояния электрической сети 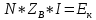 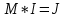 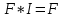 Пользуясь алгоритмом расчета установившегося режима для замкнутой сети, на основе уравнения состояния, осуществляя операцию умножения полученных матриц, получили в среде Mathcad следующие результаты: |

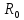 , Ом/км
, Ом/км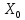 , Ом/км
, Ом/км