вопросы. Электромагнитное поле и его описание
 Скачать 0.93 Mb.
|
|
2.4. Резонанс. Частотные характеристики. Резонанс – такой режим цепи синусоидального тока, содержащей индуктивные и емкостные элементы, при котором реактивное сопротивление и проводимость равны нулю. При резонансе приложенное напряжение и входной ток совпадают по фазе. Цепи, в которых возникает явление резонанса, называют резонансными цепями или колебательными контурами. Под резонансным режимом пассивного двухполюсника понимают режим, при котором напряжение и ток на его входе совпадают по фазе. Условием резонанса является равенство нулю реактивного сопротивления X или реактивной проводимости B цепи, что предполагает наличие в цепи реактивных элементов различного характера (индуктивного и емкостного). В разветвленных цепях, где количество реактивных элементов N>3, возможны несколько резонансных режимов. Резонансный режим логично достичь либо изменением параметров элементов цепи, либо изменением частоты приложенного к цепи напряжения, либо сочетанием этих двух факторов. Резонансный режим в цепи с последовательным соединением участков, содержащих реактивные элементы различного характера, носит название резонанс напряжений. Признаком резонанса напряжения является равенство реактивных составляющих напряжений на последовательно включенных реактивных элементах различного характера. Резонансный режим с параллельным соединением таких участков называется резонансом токов. Характерным признаком резонанса токов является равенство реактивных составляющих токов в параллельных ветвях, содержащих реактивные элементы различного характера. 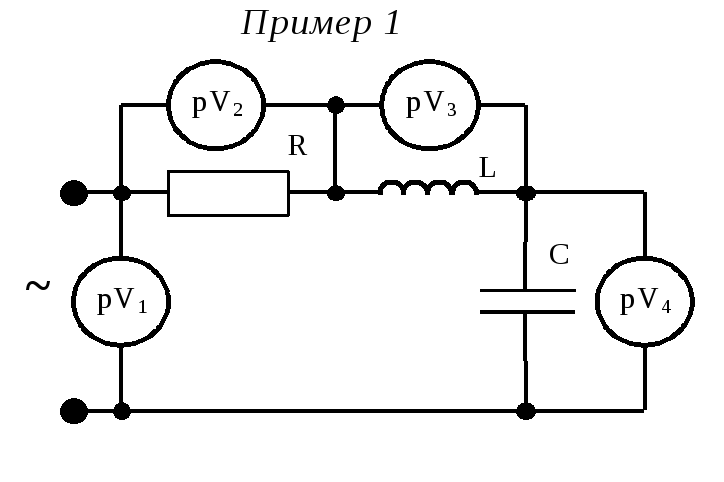 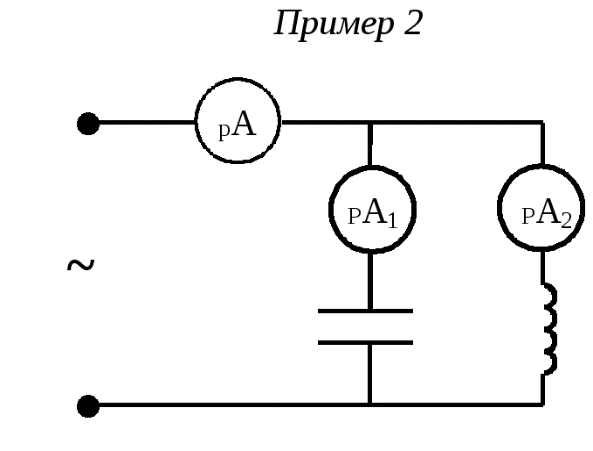 Частотные характеристики– зависимость от частоты параметров цепи. Резонансные кривые– зависимость действующих и амплитудных значений напряжений и токов от частоты или параметров цепи. Вид резонансных кривых определяется видом частотных характеристик. 2.5. Мощности. Одним из основных показателей любого электроприбора является такая физическая величина, как электрическая мощность. Ею принято называть интенсивность или скорость генерации, передачи либо преобразования электроэнергии в другие виды энергии, например, тепловую, световую, механическую. Мгновенной мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи. По определению, электрическое напряжение — это отношение работы электрического поля, совершенной при переносе пробного электрического заряда из точки A в точку B, к величине пробного заряда. То есть можно сказать, что электрическое напряжение равно работе по переносу единичного заряда из точки A в точку B. Другими словами, при движении единичного заряда по участку электрической цепи он совершит работу, численно равную электрическому напряжению, действующему на участке цепи. Умножив работу на количество единичных зарядов, мы, таким образом, получаем работу, которую совершают эти заряды при движении от начала участка цепи до его конца. Мощность, по определению, — это работа в единицу времени. Введём обозначения: U — напряжение на участке A-B (принимаем его постоянным на интервале \Delta t), Q — количество зарядов, прошедших от A к B за время \Delta t, A — работа, совершённая зарядом Q при движении по участку A-B,  P — мощность.Записывая вышеприведённые рассуждения, получаем:  Для единичного заряда на участке А-В : Для всех зарядов: 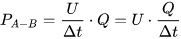 Поскольку ток есть электрический заряд, протекающий по проводнику в единицу времени, то есть 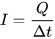 по определению, в результате получаем: Полагая время бесконечно малым, можно принять, что величины напряжения и тока за это время тоже изменятся бесконечно мало. В итоге получаем следующее определение мгновенной электрической мощности: мгновенная электрическая мощность p(t), выделяющаяся на участке электрической цепи, есть произведение мгновенных значений напряжения u(t) и силы тока i(t) на этом участке:  Если участок цепи содержит резистор c электрическим сопротивлением R, то 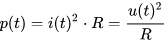 2.6. Трехфазные цепи. Схемы. Трехфазные цепи переменного тока по сей день служат для обеспечения генерации, передачи и распределения электрической энергии. Данные цепи, как следует из их названия, строятся каждая из трех электрических подцепей, в каждой из которых действует синусоидальная ЭДС. ЭДС эти генерируются общим источником, имеют равные амплитуды, равные частоты, однако смещены по фазе друг относительно друга на 120 градусов или на 2/3 пи (треть периода). Каждая из трех цепей трехфазной системы именуется фазой: первая фаза – фаза "А", вторая фаза – фаза "В", третья фаза – фаза "С". Начала этих фаз обозначаются соответственно буквами А, В и С, а концы фаз – X, Y и Z. Данные системы отличаются экономичностью, в сравнении с однофазными; возможностью простого получения вращающегося магнитного поля статора для двигателя, доступностью двух напряжений на выбор — линейного и фазного. Генератор трехфазного тока и асинхронные двигатели  Итак, трехфазный генератор представляет собой синхронную электрическую машину, предназначенную для создания трех гармонических ЭДС, смещенных на 120 градусов по фазе (по сути - во времени) друг относительно друга. На статоре генератора для этой цели установлена трехфазная обмотка, у которой каждая фаза состоит из нескольких катушек, причем магнитная ось каждой «фазы» обмотки статора физически в пространстве повернута на треть окружности относительно двух других «фаз». Такое расположение обмоток позволяет получать он них систему трехфазных ЭДС в процессе вращения ротора. Ротором здесь служит постоянный электромагнит, возбуждаемый током обмотки возбуждения, расположенной на нем. Турбина на электростанции вращает ротор с постоянной скоростью, магнитное поле ротора вращается вместе с ним, магнитные силовые линии пересекают проводники обмоток статора, в итоге получается система индуцированных синусоидальных ЭДС одинаковой частоты (50 Гц), смещенных друг относительно друга во времени на треть периода. 2.7. Соединение «звездой». Симметричные и несимметричные режимы. Симметричным режимом трехфазной цепи называют режим, при котором трехфазные системы токов и напряжений в этой цепи одновременно симметричны. Для реализации такого режима необходимо, чтобы сопротивления всех фаз были одинаковы. На рис. 11.3 приведены векторные диаграммы, характерные для цепи при симметричном режиме в случае соединения нагрузки звездой (рис. 11.3а) и треугольником (рис. 11.3б). 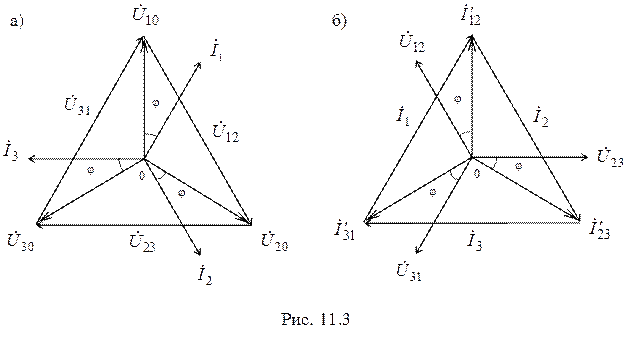 Из приведенных диаграмм следуют простые соотношения, связывающие фазные и линейные токи и напряжения в симметричных режимах. Вектора  ,  и  на рис. 11.3а образуют равнобедренный треугольник с углом 30 градусов при основании, следовательно или  Аналогичные соотношения связывают другие линейные и фазные напряжения, а также фазные токи с линейными в случае соединения треугольником, поэтому  - при соединении звездой, - при соединении треугольником .Активная мощность в случае симметричной трехфазной нагрузки определяется в виде:  или  где  - угол сдвига между фазным напряжением и фазным током.Аналогичный вид имеют выражения для реактивной и полной мощностей: 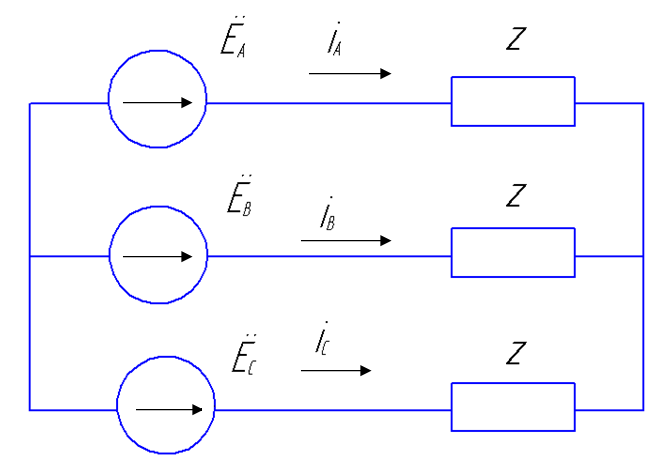 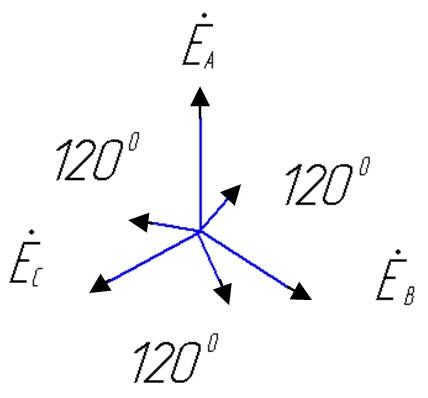  а) б) Рис. 9. Симметричный режим работы трехфазной цепи. а — трехфазная цепь; б — векторная диаграмма. 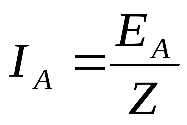 в симметричном режиме могут быть соединены как имеющие одинаковые потенциалы:2.8. Переходные процессы. Общие вопросы. При всех изменениях в электрической цепи: включении, выключении, коротком замыкании, колебаниях величины какого-либо параметра и т.п. – в ней возникают переходные процессы, которые не могут протекать мгновенно, так как невозможно мгновенное изменение энергии, запасенной в электромагнитном поле цепи. Таким образом, переходный процесс обусловлен несоответствием величины запасенной энергии в магнитном поле катушки и электрическом поле конденсатора ее значению для нового состояния цепи. При переходных процессах могут возникать большие перенапряжения, сверхтоки, электромагнитные колебания, которые могут нарушить работу устройства вплоть до выхода его из строя. С другой стороны, переходные процессы находят полезное практическое применение, например, в различного рода электронных генераторах. Все это обусловливает необходимость изучения методов анализа нестационарных режимов работы цепи. Основные методы анализа переходных процессов в линейных цепях: Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи. Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам. Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза. Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия. Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши). Первый закон коммутации обусловлен непрерывностью изменения магнитного поля катушки индуктивности и гласит: в любой ветви индуктивностью ток и потокосцепление в момент коммутации сохраняют те же значения, которые они имели непосредственно перед коммутацией, и далее начинают изменяться именно с этих значений, т.е.:  (11.1)Второй закон коммутации обусловлен непрерывностью изменения электрического напряжения и гласит: в любой ветви с ёмкостью напряжение на ёмкости и электрический заряд в момент коммутации сохраняет те значения, которые они имели непосредственно перед коммутацией, и далее начинают изменяться именно с этих значений, т.е.:  (11.2)2.9. Классический метод расчета переходных процессов. Классическим называют метод расчета переходных процессов, в котором решение дифференциального уравнения представляет собой сумму принужденной и свободной составляющей. Порядок решения задач классическим методом: Для цепи после коммутации составить систему дифференциальных уравнений по I и II законам Кирхгофа. Определить независимые начальные условия (uC иiL) из расчета режима цепи до коммутации с применением законов коммутации. Записать искомые величины в виде суммы принужденных и свободных составляющих. Найти принужденные составляющие, рассчитав установившийся режим цепи после коммутации. Составить характеристическое уравнение и вычислить его корни. В зависимости от вида корней характеристического уравнения записать свободные составляющие и искомые решения в общем виде. Для определения постоянных интегрирования записать искомые величины, их производные и систему дифференциальных уравнений для момента t=0. Подставить вычисленные постоянные интегрирования в искомые решения. Построить графики изменения токов и напряжений во время переходного процесса. Переходные процессы в Rl-цепях постоянного тока Пусть катушка индуктивности включается на постоянное напряжение (рис. 45). Определить законы изменения тока и падений напряжений на индуктивности и резисторе во время переходного процесса. По 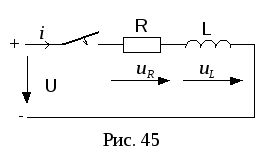 II закону Кирхгофа для послекоммутационной схемы: . ; ; .Ток переходного процесса будем искать в виде суммы принужденной и свободной составляющих. Для нахождения принужденной составляющей тока необходимо рассчитать установившийся режим после коммутации.  , т.к. в установившемся режиме при протекании постоянного тока индуктивность ведет себя как идеальный провод, падения напряжения на ней не происходит.Характеристическое уравнение:  ; его корень .Свободную составляющую тока будем искать в виде:  , где А– постоянный коэффициент, определяющийся из начальных условий.  .По первому закону коммутации: 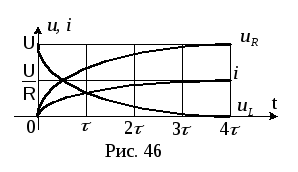 , т.к. до коммутации цель была отключена от источника ЭДС. Отсюда ; . Тогда ток через индуктивность во время переходного процесса будет изменяться по закону:  (рис. 46).Обозначим  - постоянная времени, которая определяет скорость изменения тока или напряжения во время переходного процесса. Для данной электрической цепи.  Единицы измерения постоянной времени:  |