вопросы. Электромагнитное поле и его описание

• Название: Электромагнитное поле и его описание
• Анкор: вопросы
• Дата: 06.03.2023
• Размер: 0.93 Mb.
• Имя файла: вопросы.docx
• Тип: Документы; #971390
• страница: 1 из 3

Вопросы для подготовки к зачету (экзамену)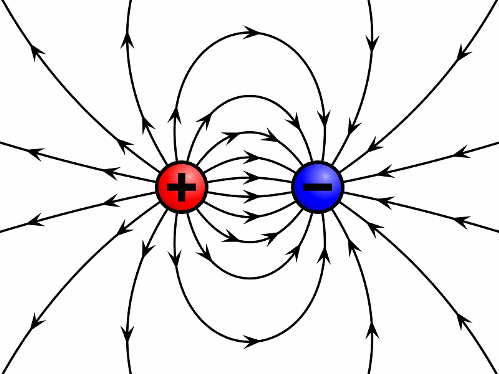

1. 
   Электромагнитное поле и его описание.
   

Электромагнитное поле – это особая форма материи, посредством которой осуществляется взаимодействие между электрически заряженными частицами.

Электрическое поле характеризуется напряженностью электрического поля (обозначение «E», размерность СИ – В/м, вектор).

Магнитное поле – создается при движении электрических зарядов по проводнику.

Магнитное поле характеризуется напряженностью магнитного поля (обозначение «H», размерность СИ – А/м, вектор). Измерению обычно подвергается модуль (длина) вектора. Электромагнитные волны характеризуются длиной волны (обозначение «l», размерность СИ - м), излучающий их источник – частотой (обозначение – «n», размерность СИ - Гц). На рисунке Е – вектор напряженности электрического поля, H– вектор напряженности магнитного поля.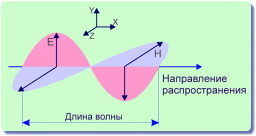

Физической причиной существования электромагнитного поля является то, что изменяющееся во времени электрическое поле возбуждает магнитное поле, а изменяющееся магнитное поле – вихревое электрическое поле. Непрерывно изменяясь, обе компоненты поддерживают существование электромагнитного поля. Поле неподвижной или равномерно движущейся частицы неразрывно связано с носителем (заряженной частицей).

При частотах 3 – 300 Гц в качестве характеристики магнитного поля может также использоваться понятие магнитной индукции (обозначение «B», размерность СИ - Тл).

, , , , ,

1.1. Электрические и магнитные цепи.

Электрической цепью называется совокупность устройств, предназначенных для передачи, распределения и взаимного преобразования электромагнитной электроэнергии, образующих путь для электрического тока.

Магнитной цепью называется устройство, отдельные участки которого выполнены из ферромагнитных материалов, по которым замыкается магнитный поток. Примерами простейших цепей могут служить магнитопроводы кольцевой катушки и электромагнита.

Для того чтобы заряды перемещались им необходимо передать некоторую энергию и устройство, выполняющее эту функцию, называется источником электрической энергии. Источник электрической энергии является составным элементом электрической цепи. Энергия, передаваемая источником движущимся зарядам, может быть получена только путём преобразования других видов энергии (тепловой, химической, механической, световой) или путём воздействия на электрические заряды магнитным полем, возбуждаемым другим источником. Создаваемый источником электрический ток может вызывать различные явления: нагревать элементы, по которым он протекает, вызывать свечение веществ, создавать механические усилия. Технические устройства, в которых получают требуемый эффект от протекания электрического тока называют приёмниками электрической энергии, т.к. в них происходит преобразование электрической энергии в другие виды. Совместная работа источника и приёмника возможна только при наличии путей движения зарядов между ними. Причём, перемещение зарядов должно происходить с минимальными потерями энергии. Эту функцию в электрических цепях выполняют соединительные линии или провода.

Таким образом, электрическая цепь в общем случае состоит из трёх элементов: источника электрической энергии, приёмника и соединительных проводов.


1.2. Связи характеристик поля и цепей.

Любая электрическая цепь и каждый ее элемент в отдельности обладают тремя параметрами: сопротивлением R, индуктивностью L и емкостью С. Сопротивление R характеризует способность цепи преобразовывать электромагнитную энергию в тепловую. Индуктивность L характеризует способность цепи накапливать энергию магнитного поля. Такой способностью обладает любой проводник с током или система проводов. Емкость С характеризует способность цепи накапливать энергию электрического поля. Такой способностью обладают любые два провода, разделенные диэлектриком, например провод, висящий над землей, любые два провода линии передачи.

Примеры нелинейных характеристик для нелинейных резисторов, индуктивностей и конденсаторов

представлены на рис.3.1.

Математический аппарат для расчета линейных цепей – это линейные алгебраические и

дифференциальные уравнения. Для расчета нелинейных соответственно – нелинейные

алгебраические и дифференциальные уравнения.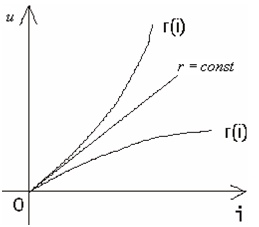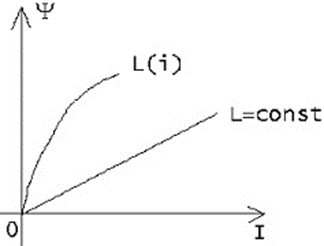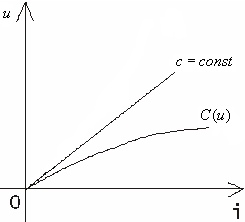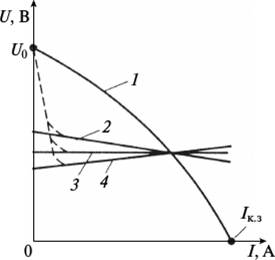


1.3. Внешние характеристики источников.

Внешняя характеристика отражает зависимость напряжения на зажимах источника от величины нагрузки - тока источника, заданного нагрузкой. Напряжение на зажимах источника меньше ЭДС на величину падения напряжения на внутреннем сопротивлении источника (1):




В зависимости от конструкции источников питания внешние характеристики могут быть (рис. 1.5) крутопадающими 1, пологопадающими 2, жесткими 3 и возрастающими 4.
Этому уравнению соответствует внешняя характеристика источника ЭДС (рис. 1). построенная по двум точкам:

1) при I=0 E=U;

2) при U=0 E=R0I .

Очевидно, что напряжение на зажимах источника ЭДС тем больше, чем меньше его внутреннее сопротивление.

В идеальном источнике ЭДС R0=0, U=E (напряжение не зависит от величины нагрузки). Однако не всегда при анализе и расчете цепи источник электрической энергии удобно представлять в качестве источника ЭДС. Если внутреннее сопротивление источника значительно превышает внешнее сопротивление цепи, что, например, имеет место в электронике, то получим, что ток в цепи I=U/(R+R0) и при R0>>R практически не зависит от сопротивления нагрузки. В этом случае источник энергии представляют в качестве источника тока.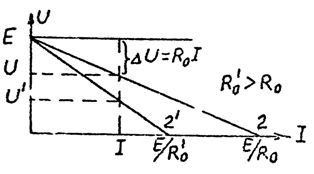



1.4. Условия эквивалентности источников.

Теорема об эквивалентном источнике

Применяется, когда требуется найти ток в заданной одной ветви. Суть теоремы в том, что по отношению к выделенной ветви Z_ab , вся остальная часть любой сложной схемы заменяется одним эквивалентным генератором с ЭДС E_э и внутренним сопротивлением Z_э .

Покажем это. Пусть Z_ab -связь и входит в контур 1. Тогда Z₁₁ = Z_ab + Z⁰₁₁ и Z⁰₁₁ есть собственное сопротивление контура при Z_ab  0 .Так как Z_ab -связь, то она не входит ни в какие другие элементы матрицы контурных сопротивлений.
В соответствии с теоремой об эквивалентном источнике ток произвольной ветви линейной электрической цепи не изменится, если автономный двухполюсник, к которому подключена данная ветвь, заменять эквивалентным линеаризованным источником, который может быть представлен последовательной или параллельной схемами замещения.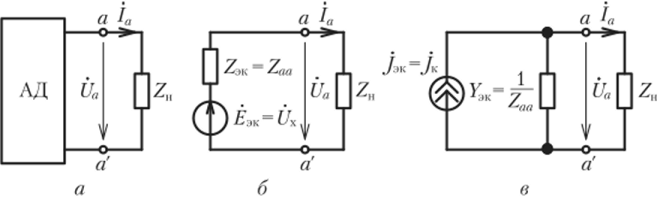



1.5. Гармонические напряжения, токи.

Гармонические колебания тока или напряжения могут быть описаны одной из функций





Обе записи равноправны, однако при решении задач следует придерживаться какой-либо одной из них. Мы будем пользоваться первой.

Наибольшее по абсолютному значению отклонение колеблющейся величины называется её амплитудой и обозначается 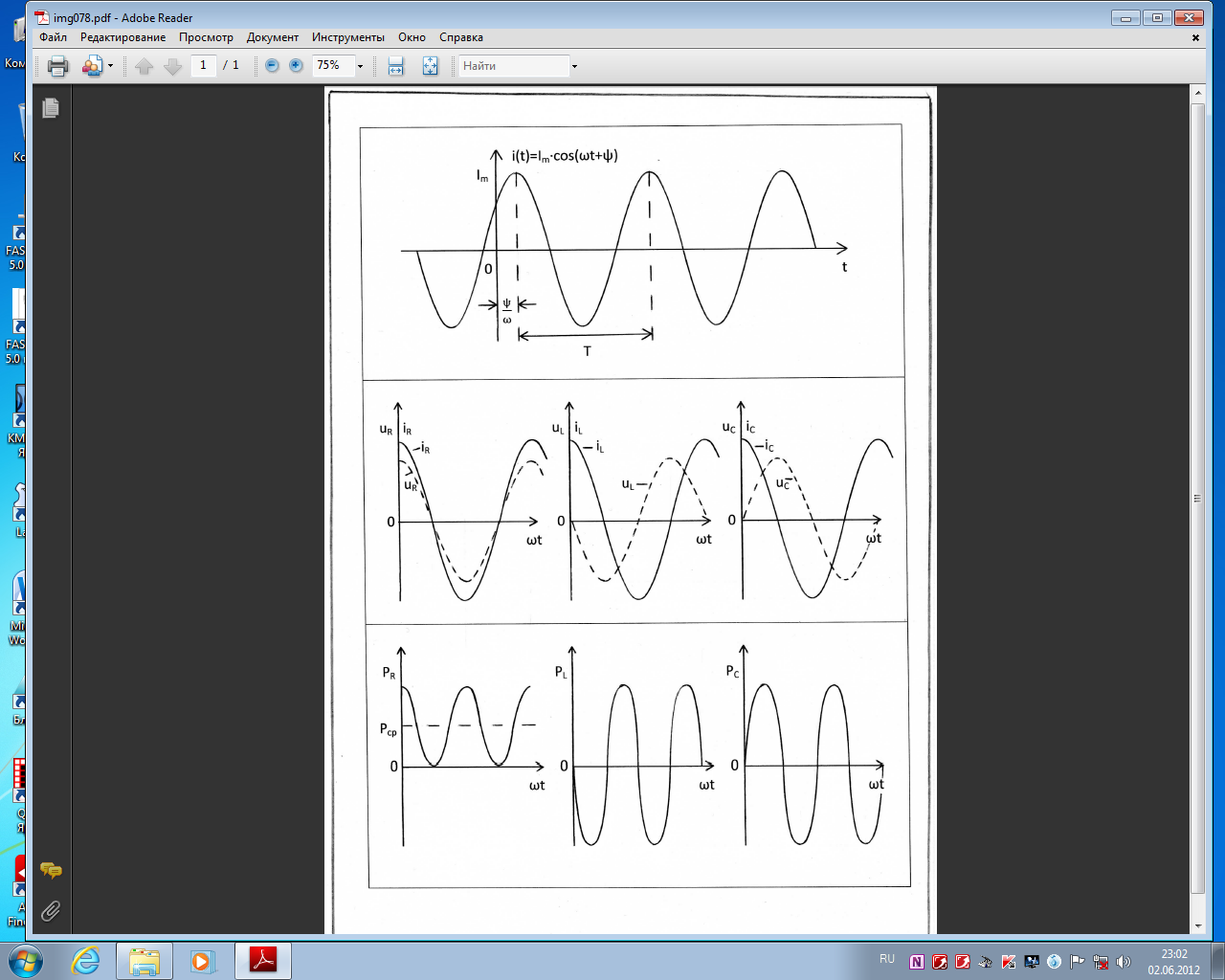  (   ). Наименьшее значение времени, после которого процесс полностью повторяется (время одного цикла колебания), называется периодом колебания Т (рис. 3.1). Число циклов колебания в единицу времени называется циклической частотой колебания   или просто частотой. Частота измеряется в герцах (Гц). Герц – одно колебание в секунду. Число циклов колебания в интервале, равном 2π единицам времени, называется угловой частотой

 

Величина   называется фазой колебания. Значение фазы колебания в момент времени   называется начальной фазой колебания.

Действующим значением любого периодического тока (напряжения) называется его среднеквадратичное значение за период 

 

1.6. Связи между напряжениями и токами на пассивных элементах.

В теории электрических цепей различают активные и пассивные элементы. Первые вносят энергию в электрическую цепь, а вторые ее потребляют.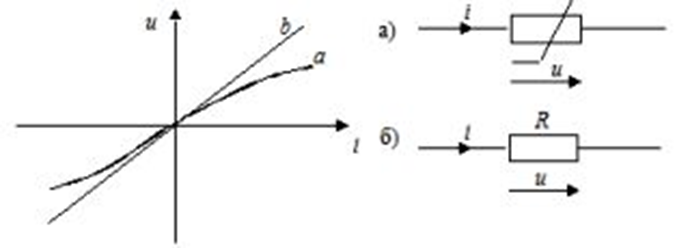

Резистивным сопротивлением называется идеализированный элемент электрической цепи, обладающий свойством необратимого рассеивания энергии. Графическое изображение этого элемента и его вольт-амперная характеристика показана на рисунке (а - нелинейное сопротивление, б -линейное сопротивление).

Напряжение и ток на резистивном сопротивлении связаны между собой зависимостями: u = iR, i = Gu. Коэффициенты пропорциональности R и G в этих формулах называются соответственно сопротивлением и проводимостью и измеряются в омах [Ом] и сименсах [См]. R = 1/G.

Активные элементы электрических цепей

Активными называются элементы цепи, которые отдают энергию в цепь, т.е. источники энергии. Существуют независимые и зависимые источники. Независимые источники: источник напряжения и источник тока.

Источник напряжения - идеализированный элемент электрической цепи, напряжение на зажимах которого не зависит от протекающего через него тока.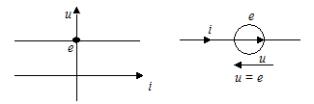



Внутреннее сопротивление идеального источника напряжения равно нулю.

Источник тока – это идеализированный элемент электрической цепи, ток которого не зависит от напряжения на его зажимах.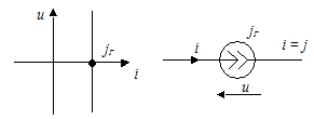



Внутреннее сопротивление идеального источника тока равно бесконечности.

Источники напряжения (тока) называются зависимыми (управляемыми), если величина напряжения (тока) источника зависит от напряжения или тока другого участка цепи. Зависимыми источниками моделируются электронные лампы, транзисторы, усилители, работающие в линейном режиме.

1.7. Законы теории цепей.
Основные законы теории электрических цепей – это закон Ома и законы Кирхгофа.

Согласно закону Ома, для участка цепи, не содержащего ЭДС, ток I прямо пропорционален напряжению U на этом участке и обратно пропорционален сопротивлению R этого участка

.

Если на участке цепи имеются эдс, то для расчёта тока применяют обобщённый закон Ома:

,

где 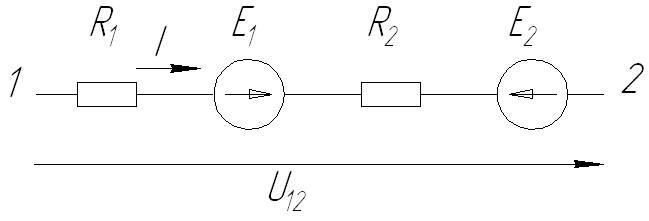 – алгебраическая сумма эдс на участке 1–2 (см. рис.);

– напряжение на участке 1–2;

– арифметическая сумма сопротивлений всех резисторов участка 1–2.



Если эдс и напряжения совпадают по направлению с условно положительным направлением тока, они берутся со знаком плюс, если они противоположны условно положительному направлению тока, то со знаком минус. Для схемы, представленной выше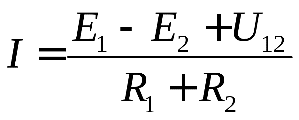

.

1. Первый закон Кирхгофа

Алгебраическая сумма мгновенных значений токов ветвей, сходящихся в одном узле, равна нулю: .

Токи, входящие в узел, берутся с одним знаком, а выходящие – с противоположным.

2. Второй закон Кирхгофа

Алгебраическая сумма мгновенных значений напряжений на всех элементах контура равна нулю: .

Выбирают направление обхода контура и тогда напряжения, совпадающие с направлением обхода контура, берут со знаком плюс, а направленные навстречу – со знаком минус. Так как напряжение на источнике ЭДС в точности равно самой ЭДС, а направлено в обратную сторону, удобно применять другую формулировку второго закона Кирхгофа: Алгебраическая сумма мгновенных значений напряжений на всех элементах контура, кроме источников ЭДС, равна алгебраической сумме мгновенных значений ЭДС этого же контура.

1.8. Граф. Топологические матрицы.
Режим электрической цепи произвольной конфигурации полностью оп­ределяется первым и вторым законами Кирхгофа. Вид уравнений электри­ческого состояния цепи, составленных по этим законам, зависит только от схемы соединения элементов (ветвей), т. е. от топологической структуры цепи, и не зависит от вида и параметров самих эле­ментов. В таком случае ветви, содержащие различные элементы, можно представлять просто линиями, а структуру цепи – совокупностью этих линий, которая называется графом электрической цепи.

При машинном способе формирования уравнений, описывающих элект­ромагнитные процессы в электрических цепях, иногда рассматривают каж­дый двухполюсный элемент как отдельную ветвь. В этом случае принимают во внимание все узлы, включая устранимые. Такое топологическое описа­ние цепи называется расширенным. При сокращенном топологи­ческом описании группы последовательно соединенных элементов рассмат­ривают в качестве отдельных ветвей, а устранимые узлы в расчет не принимаются.

Любой двухполюсный элемент или группа последовательно соединен­ных элементов на графе электрической цепи изображается отрезком ли­нии, который называется ветвью или ребром. Точки соедине­ния ветвей являются узлами (вершинами) графа. Таким образом,  граф есть совокупность узлов, соединенных друг с другом ветвями. В теории электрических цепей в основном на­ходят применение направленные (ориентированные) графы, у которых каждая ветвь имеет определенную ориента­цию, указанную стрелкой. Для графов электрических цепей направ­ление каждой ветви выбирается совпадающим с положительным направлением тока в соответствующей ветви электрической схемы.

Если ветвь и узел графа соприкасаются, то говорят, что они инцидентны.

Граф электрической цепи строят по ее эквивалентной схеме. Каждой ветви схемы соответствует ветвь (ребро) графа, а каждому узлу схемы – узел (вершина) графа. Ветви графа с помощью стрелок ориентируют в со­ответствии с положительным направлением токов, протекающих по соот­ветствующим ветвям схемы. На топологической схеме источники ЭДС и тока не изображаются. При этом ветви с источниками ЭДС сохраняются. Ветви же с идеальными источниками тока вообще не включаются в граф схемы, т.к. сопротивление таких ветвей бесконечно велико.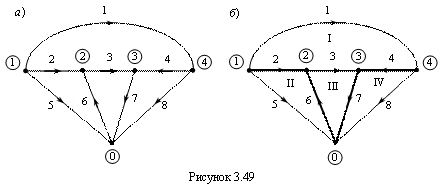



Топологические матрицы

Для аналитического описания структуры электрической цепи, ее гра­фа и основных законов токораспределения применяют топологические матрицы.

Аналитическое представление графа необходимо для формирования уравнений сложной цепи с помощью ЭВМ.

В соответствии с видом уравнений Кирхгофа различают три топологичеcкие­ матрицы: соединений (узловую матрицу) [А], контурную (главных кон­туров) [В] и главных сечений [Q].

Полное описание структуры направленного графа дает [nУ × nВ]-матрица соединений, nУ строк которой являются поряд­ковыми номерами узлов, а nВ столбцов – номерами ветвей. Она представ­ляет собой таблицу коэффициентов уравнений, составленных по первому закону Кирхгофа для узлов схемы. Элемент матрицы aij, расположенный на пересече­нии i-й строки и j-го столбца, равен +1, если ветвь j графа соединена с узлом i и направлена от узла. Элемент матрицы aij = –1, если ветвь j соединена с узлом i и направлена к узлу. Элемент матрицы aij = 0, если ветвь j не присоединена к узлу i. Для графа на рисунке 3.49 полу­чим полную матрицу соединений:

   (3.42)

В каждом столбце матрицы [а0] имеется только два ненулевых элемента: +1 и –1, т. к. каждая ветвь инцидентна двум узлам и направлена от од­ного к другому. Сумма элементов каждого столбца матрицы [А0] равна ну­лю, т. е. строки полной матрицы являются линейно зависимыми. Из этого следует, что достаточно заполнить таблицу для (nУ – 1) узлов, которая является редуцированной (сокращенной) матрицей соеди­нений [А]. Она получается из полной матрицы соединений путем вычерки­вания строки, соответствующей выбранному базисному узлу. Вычеркивая последнюю строку в матрице (3.42), получим редуцированную матрицу соединений (узловую матрицу) [а]:

  (3.43)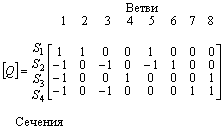

Матрица главных сечений [Q] представляет собой таблицу коэф­фициентов, составленных по первому закону Кирхгофа для главных сечений. Стро­ки матрицы [Q] соответствуют сечениям, столбцы – ветвям. Элемент мат­рицы qij = +1, если ветвь j содержится в сечении i и ее ориентация совпадает с ориентацией сечения, т. е. ориентацией соответствующей ветви дерева относительно линии сечения. Элемент матрицы qij = –1, ес­ли ветвь j содержится в сечении i и направлена противоположно направ­лению сечения. Элемент матрицы qij = 0, если ветвь j не содержится в сечении i. Запишем матрицу главных сечений для рисунка 3.50:

  (3.44)

Матрица главных контуров (контурная матрица) [B] – это таблица коэффициентов уравнений, составленных по второму закону Кирхгофа. Стро­ки матрицы [B] соответствуют главным контурам, столбцы – ветвям. Элемент мат­рицы bij = +1, если ветвь j содержится в сечении i и направление ветви совпадает с направлением обхода контура. Элемент матрицы bij = –1, ес­ли ветвь j содержится в сечении i и направление ветви противоположно направ­лению обхода контура. Элемент матрицы bij = 0, если ветвь j не содержится в контуре i. Составим контурную матрицу для рисунка 32.3.9:

   (3.45)