вопросы. Электромагнитное поле и его описание
 Скачать 0.93 Mb.
|
|
1.9. Полная система уравнений цепи. Для вычисления всех токов и напряжений в эл. цепи в общем случае нужно решить систему уравнений. Онаназывается полной системой расчетных уравнений эл. цепи. Ее можно записывать в разных формах. Мы рассмотрим классический вариант, когда система состоит из уравнений узлов и уравнений контуров. При этом ограничимся цепями, образованными соединением двухполюсников. Прежде чем записывать уравнения, на всех ветвях схемы поставим стрелки тока и на всех элементах схемы поставим (или мысленно представим себе) стрелки напряжения. Затем составим уравнения системы, которые вначале разделим на три группы.
2) Уравнения контуров – это уравнения, составленные по 2-му закону Кирхгофа для всех независимых контуров эл. цепи. Для цепи, схема которой нарисована без пересечения проводов, независимые контуры могут быть выбраны с помощью штриховки, линии которой не пересекают провода и элементы эл. цепи (рис.7.2). Согласно штриховке рис. 7.2 на схеме рис. 7.1 выберем контуры, образованные ветвями, соединяющими узлы: 1-2, 2-3, 3‑1 (контур №1); 1-2, 2-4, 4-1 (контур №2); 3-2, 2‑4, 4-3 (контур №3). Запишем уравнения этих контуров:
3) Уравнения элементов. В полную систему расчетных уравнений цепи включаются уравнения всех ее элементов. Пример: Уравнения элементов для цепи, изображенной на рис. 7.1:  (7.3)Всего для схемы рис. 7.1 получаем 14 уравнений с 14 неизвестными. Это наиболее общая, но и самая громоздкая запись полной системы расчетных уравнений цепи. Уравнения элементов (7.3) часто сразу подставляют в уравнения контуров (7.2), выражая напряжения через токи. В результате вместе с уравнениями узлов (7.1) получается классическая форма полной системы расчетных уравнений цепи. Ее часто называют системой уравнений Кирхгофа для эл. цепи:   (7.4)2.0. Расчет установившихся процессов во временной области. Под установившимся режимом электрической сети понимается такой нормальный или послеаварийный режим, в котором токи, напряжения и мощности в ее элементах принимаются неизменными. Расчет установившегося режима подразумевает определение этих токов, напряжений и мощностей, которые характеризуют режим электрической сети называются параметрами режима. Целями и задачами расчета установившегося режима электрической сети являются: •проверка допустимости параметров режима для элементов сети, в частности проверка допустимости величин напряжений по условиям работы изоляции, величин токов − по условиям нагрева проводов, величин мощностей − по условиям работы источников активной и реактивной мощности; •оценка качества электроэнергии путем сравнения отклонений напряжений в сети с допустимыми отклонениями напряжений от номинальных значений; •определение экономичности режима по величинам потерь мощности и электроэнергии в электрической сети. Исходными данными для расчета установившегося режима электрической сети являются: •принципиальная схема электрической сети, характеризующая взаимную связь между отдельными ее элементами; •расчетная схема замещения электрической сети, состоящая из схем замещения отдельных элементов, т.е. из сопротивлений, проводимостей, коэффициентов трансформации, называемых параметрами схемы замещения электрической сети; •значения активных и реактивных мощностей в узлах нагрузки; •значения активных и реактивных мощностей источников питания, кроме одного, называемого балансирующим по мощности и покрывающим небаланс между вырабатываемой и потребляемой в ЭЭС мощностями; •значение напряжения в одном из узлов электрической сети, называемом базисным узлом по напряжению. Электрическая сеть с позиций теоретической электротехники является электрической цепью и для ее расчета справедливы законы Ома и Кирхгофа и все методы расчета электрических цепей, известные из теоретической электротехники. Электрическая сеть (электрическая цепь) состоит из ветвей, узлов и контуров. Ветвью называется участок сети, состоящий из последовательно соединенных элементов, по которым протекает один и тот же ток. Узлом называют место соединения двух или более ветвей. Контуром называют замкнутый участок сети, состоящий из нескольких ветвей. Электрическая сеть, не содержащая контуров, называется разомкнутой (рис. 3.4,а,б). В такой сети каждый узел нагрузки получает питание с одной стороны (от одного источника). Замкнутая сеть содержит контуры. Простейшая замкнутая сеть – это кольцевая сеть (рис. 3.4,в), в которой каждый узел нагрузки получает питание с двух сторон. В сети с двухсторонним питанием (рис. 3.4,г) каждый узел нагрузки получает питание с двух сторон от разных источников питания. Сложнозамкнутая сеть (рис. 3.4,д) содержит не менее двух контуров с общими ветвями. Нагрузки в такой сети могут получать питание с двух и более сторон. Наибольшее распространение для расчета любых электрических сетей получил итерационный метод или метод последовательных приближений. В этом методе искомые величины определяются в результате повторяющейся вычислительной процедуры (итерации). На первой итерации осуществляется переход от начальных приближений к более точным значениям искомых величин. На последующих итерациях эти значения последовательно уточняются. Вычислительная процедура заканчивается при достижении заданной точности вычислений. Начальные приближения могут задаваться на основании тех или иных представлений о возможных значениях искомых величин. Так, в частности, начальные значения искомых напряжений в узлах электрической сети могут быть заданы равными номинальному напряжению этой сети. 2.1. Расчет установившихся режимов с помощью комплексных чисел. Поскольку на практике выполнять математические операции с гармоническими (синусоидальными) функциями неудобно, в расчетах используется преобразование, позволяющее представить реальную синусоидальную величину, являющуюся функцией времени (оригинал), в виде некоторой эквивалентной величины на комплексной плоскости (изображение). Синусоидальный ток можно представить, как «след» вектора, вращающегося против часовой стрелки с угловой скоростью w. Тогда от операций с синусоидальными величинами можно перейти к операциям с векторами. (Рисунок 1) 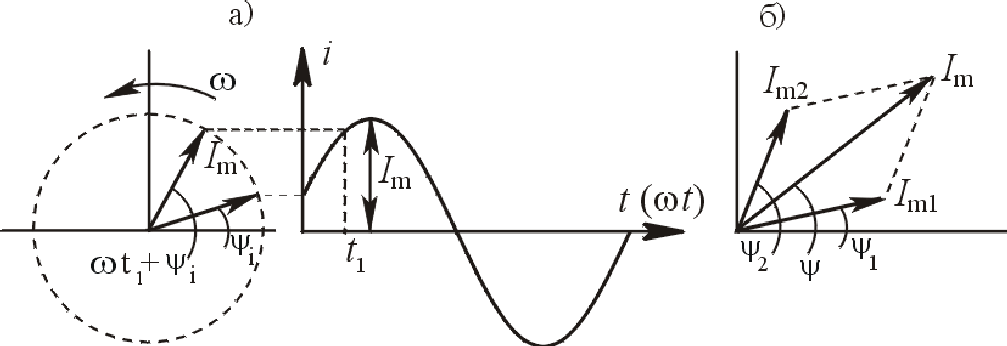 Рисунок 1 – Представление синусоидального тока Поскольку в одной цепи у всех токов и напряжений угловая частота ω будет одинаковой (соответствует частоте приложенного воздействия), самим фактом вращения вектора можно пренебречь и перейти от синусоидальной величины к вектору на комплексной плоскости. Общий вид вектора на комплексной плоскости представлен на рисунке 2: 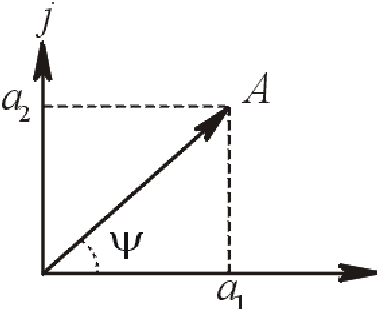 Рисунок 2 – общий вид вектора на комплексной плоскости По горизонтальной оси откладывается действительная часть a1= Re(A), по Вертикальной – мнимая часть a2= Im(A). Само числоA может быть записано в виде: A = a1+ ja2, где j — мнимая единица: j =  Комплексные числа можно записывать в трех различных формах. Основными формами записи являются алгебраическая: A=a1+ ja2 Экспоненциальная: A=  , |A|= ,ψ=arctg  Связь между ними обеспечивает тригонометрическая форма записи: A=∣A∣cos(ψ)+ j∣A∣sin(ψ) В электротехнике для того, чтобы отличать комплексные изображения токов и напряжений их принято обозначать «точечкой» или «кружочком» над величиной (старый стандарт) или подчеркивать снизу (новый стандарт): Ů , I̊ или U,I Переход от оригинала к изображению: u (t)=Um sin(ω t+ψu)→Ům=Um  2.2. Методы узловых напряжений и контурных токов. 1. Метод контурных токов. Число уравнений, составленных по законам Кирхгофа, равно числу ветвей с неизвестными токами b n . Для уменьшения числа уравнений в качестве переменных цепи используют другие величины контурные токи и узловые напряжения или узловые потенциалы. Метод контурных токов (МКТ) основан на использовании уравнений равновесия напряжений в контурах, в которых протекают независимые друг от друга контурные токи. Идея метода контурных токов: уравнения составляются только по второму закону Кирхгофа, но не для действительных, а для воображаемых токов, циркулирующих по замкнутым контурам, т.е. в случае выбора главных контуров равных токам ветвей связи. Число уравнений равно числу независимых контуров, т.е. числу ветвей связи графа  . Первый закон Кирхгофа выполняется автоматически. Контуры можно выбирать произвольно, лишь бы их число было равно  и чтобы каждый новый контур содержал хотя бы одну ветвь, не входящую в предыдущие. Такие контуры называются независимыми. Их выбор облегчает использование топологических понятий дерева и ветвей связи.Направления истинных и контурных токов выбираются произвольно. Выбор положительных направлений перед началом расчета может не определять действительные направления токов в цепи. Если в результате расчета какой-либо из токов, как и при использовании уравнений по законам Кирхгофа, получится со знаком “-”, это означает, что его истинное направление противоположно. 2. Метод узловых потенциалов Данный метод вытекает из первого закона Кирхгофа. В качестве неизвестных принимаются потенциалы узлов, по найденным значениям которых с помощью закона Ома для участка цепи с источником ЭДС затем находят токи в ветвях. Поскольку потенциал – величина относительная, потенциал одного из узлов (любого) принимается равным нулю. Таким образом, число неизвестных потенциалов, а следовательно, и число уравнений равно  , т.е. числу ветвей дерева  .Как и по методу контурных токов, система уравнений по методу узловых потенциалов может быть составлена формальным путем. При этом необходимо руководствоваться следующими правилами: 1. В левой части i-гоуравнения записывается со знаком “+”потенциал  i-го узла, для которого составляется данное i-е уравнение, умноженный на сумму проводимостей  ветвей, присоединенных к данному i-му узлу, и со знаком “-”потенциал  соседних узлов, каждый из которых умножен на сумму проводимостей  ветвей, присоединенных к i-му и k-му узлам.Из сказанного следует, что все члены  , стоящие на главной диагонали в левой части системы уравнений, записываются со знаком “+”, а все остальные – со знаком “-”, причем  . 2. В правой части i-гоуравнения записывается так называемый узловой ток  , равный сумме произведений ЭДС ветвей, подходящих к i-му узлу, и проводимостей этих ветвей. При этом член суммы записывается со знаком “+”, если соответствующая ЭДС направлена к i-му узлу, в противном случае ставится знак “-”. Если в подходящих к i-му узлу ветвях содержатся источники тока, то знаки токов источников токов, входящих в узловой ток простыми слагаемыми, определяются аналогично.В заключение отметим, что выбор того или иного из рассмотренных методов определяется тем, что следует найти, а также тем, какой из них обеспечивает меньший порядок системы уравнений. При расчете токов при одинаковом числе уравнений предпочтительнее использовать метод контурных токов, так как он не требует дополнительных вычислений с использованием закона Ома. Метод узловых потенциалов очень удобен при расчетах многофазных цепей, но не удобен при расчете цепей со взаимной индуктивностью. 2.3. Принцип наложения. Чтобы составить общее выражение для тока в k-ветви сложной схемы, составим уравнения по методу контурных токов, выбрав контуры так, чтобы k-ветвь входила только в один k-контур (это всегда возможно). Тогда согласно (2.5) ток в k-ветви будет равен контурному току Ikk. Каждое слагаемое правой части (2.5) представляет собой ток, вызванный в k-ветви соответствующей контурной ЭДС. Например, E11 Δk1/Δ есть составляющая тока k-ветви, вызванная контурной ЭДС E11. Каждую из контурных ЭДС можно выразить через ЭДС ветвей Е1, E2, E3, ... , Ek, ... , En, сгруппировать коэффициенты при этих ЭДС и получить выражение следующего вида: Ik = E1gk1 + E2gk2 +E3gk3 + ... + Ekgkk + Engkn (2.7) Если контуры выбраны таким образом, что какая-либо из ЭДС, например Еm, входит только в один m-контур, а в другие контуры не входит, то gkm = Δkm/Δ. Уравнение (2.7) выражает собой принцип наложения. Принцип наложения формулируется следующим образом: ток в k-ветви равен алгебраической сумме токов, вызываемых каждой из ЭДС схемы в отдельности. Этот принцип справедлив для всех линейных электрических цепей. Принцип наложения положен в основу метода расчета, получившего название метода наложения. При расчете цепей данным методом поступают следующим образом: поочередно рассчитывают токи, возникающие от действия каждой из ЭДС, мысленно удаляя остальные из схемы, но оставляя в схеме внутренние сопротивления источников, и затем находят токи в ветвях путем алгебраического сложения частичных токов. Заметим, что методом наложения нельзя пользоваться для подсчета выделяемых в сопротивлениях мощностей как суммы мощностей от частичных токов, поскольку мощность является квадратичной функцией тока (Р = RI2). Если через некоторое сопротивление R протекают согласно направленные частичные токи I1 и I2, то выделяемая в нем мощность Р = R(I1 + I2)2 и не равна сумме мощностей от частичных токов:  . |
Рис. 7.1.
Узел № 2: 
(7.1) Узел № 3: 
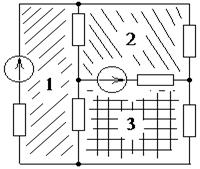Рис. 7.2.
