электротехника. конспект. Электротехника. Электротехника
 Скачать 1.13 Mb.
|
|
Обращая внимание на КПД электроцепи, нужно отметить, что он напрямую зависит от физических величин, определяющих скорость передачи или трансформации электрической энергии. Одной из таких величин является мощность Р (Вт). Формулы мощности: P = U * I = U2/R = I2 * R, где: U – напряжение на нагрузке, В; I – ток, А; R – сопротивление нагрузки, Ом. Для разных цепей значения напряжения и сила тока различаются, следовательно, производимая ими работа будет разной. Когда предстоит оценить скорость передачи и преобразования электрического тока, то обращают внимание на Р. Она соответствует работе, проделанной за единицу времени: P = A/∆t, где: P – мощность, Вт; A – работа, Дж; ∆t – временной интервал, с. Исходя из этой формулы, чтобы найти работу А, нужно умножить Р на время: A=P∙∆t Чтобы найти КПД (η) электроцепи, нужно найти отношение полезно потраченной энергии к количеству всей энергии, поданной в цепь. Формула для расчёта: η = A/Q *100%, где: А – проделанная потребителем работа, Дж; Q – количество энергии, взятой от источника, Дж. Наглядно это можно объяснить на примере электрической цепи, в которую включен проводник, имеющий определённое сопротивление. При прохождении электричества через цепь часть энергии будет рассеиваться на проводнике, превращаясь в тепло и нагревая его. Потери мощности будут зависеть от величины этого сопротивления. 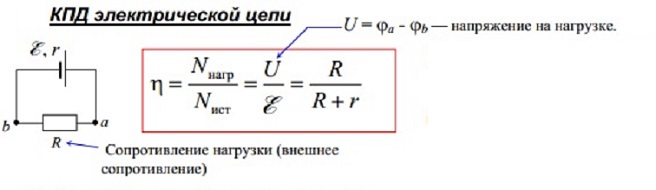 Основными режимами работы электрической цепи (рис. 1.21) являются следующие: 1.Режим номинальной нагрузки (номинальный режим). Номинальный режим характеризуется номинальным напряжением Uн, номинальным током Iн, номинальной мощностью Рн, которые указываются на табличке приемника. Номинальное напряжение сети Uн для большинства приемников постоянного тока составляет 27, 110, 220, 440 В, а также 6, 12, 24, 36 В. Номинальный ток Iн – предельно допустимый ток, при котором приемник может работать длительное время. Номинальная мощность Pн – величина, определяемая номинальным напряжением Uн и номинальным током Iн : Pн = Uн · Iн . В некоторых случаях на приемниках указывается номинальный коэффициент полезного действия – ηн , например, на электродвигателях. 2. Режим холостого хода. Режим холостого хода наблюдается в цепи при Rнагр = ∞, в этом случае I = 0, η = 100%. 3. Согласованный режим. Согласованный режим работы применяется в радиотехнических цепях, устройствах автоматики и телемеханики, в других слаботочных цепях, где необходимо передать от источника к приемнику наибольшую мощность. Это условие выполняется при равенстве сопротивлений линии и нагрузки: Rл = =Rнагр , следовательно, Uл = Uнагр и Pл = Рнагр . Коэффициент полезного действия η = 50%. 4. Режим короткого замыкания. Режим короткого замыкания возникает при коротком замыкании нагрузки (Rнагр= 0). Ток в линии ограничивается сопротивлением проводов и намного превышает номинальный:  .Напряжение сети U = Uл , следовательно, P = Pл и η = 0. При возникновении короткого замыкания линия должна отключаться от сети автоматическими выключателями (автоматами) или плавкими предохранителями. Остальные режимы являются промежуточными. Для всех режимов работы справедливы следующие уравнения. Напряжение на входе линии:  ,где: Uл– падение напряжения в линии; Uнагр – напряжение на нагрузке. Ток в линии:  ,где: Rл – сопротивление проводов линии; Rнагр – сопротивление нагрузки. Мощность, потребляемая всей цепью: P = Pл + Pнагр . где: Pл – мощность, выделяемая в проводах линии; Pнагр – мощность, потребляемая нагрузкой. Коэффициент полезного действия:  .Линии передачи выполняются в основном медными и алюминиевыми проводами. Сопротивление провода зависит от его длины l, площади поперечного сечения S и удельного сопротивления ρ:  [Ом],где l, м; S, мм2; ρ,  .Сопротивление металлического провода зависит также от температуры: с повышением температуры сопротивление провода линии увеличивается:  ,где t – температура провода, оС; α – температурный коэффициент; Rпр – сопротивление провода при 20оС. Основные параметры синусоидально изменяющихся величин. Фаза (мгновенный фазовый угол) гармонической функции в радианах (рад) или градусах – это аргумент синусоидальной функции, отсчитываемый от нулевого значения функции в положительном направлении: ωt + ψu и ωt + ψi и т.д. Начальная фаза - ψ ( начальный фазовый угол) – это значение фазы при t=0. Начальная фаза – алгебраическая величина, т.е. имеет знак. Сдвиг фаз между двумя гармоническими функциями – это разность начальных фаз двух синусоидальных функции, например, U1 и U2, т.е.: ψu = ψu1 - ψu2. Сдвиг фаз φ величина алгебраическая. Мгновенное значение синусоидального напряжения (тока, ЭДС) – это значение функции в рассматриваемый момент времени. Фактически мгновенное значение – это точка на графике функции в любой момент времени. Мгновенное значение тока, напряжения и ЭДС: i(t), u(t), e(t). Амплитуда гармонического напряжения (тока, ЭДС) – наибольшее значение синусоидальной функции, обозначаемое соответствующей прописной буквой с индексом m: Um ( Im, Em ). Амплитуда может быть как положительной, так и отрицательной. Действующее значение гармонической функции - это его среднеквадратичное значение за время Т, т.е.: I = Im / √2 ≈ 0,707Im, U = Um / √2 ≈ 0,707Um, E = Em / √2 ≈ 0,707Em. 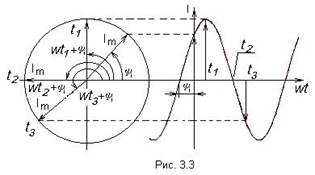 За средние значения тока, ЭДС и напряжения принимают среднее арифметическое значение соответствующей величины за полпериода (среднее значение за период, равно нулю): Eср = 2Em/π = 0,637Em, Iср = 2Iт /π = 0,637Im, Uср = 2Uт /π = 0,637Uт.Формы представления синусоидальных функций. Закон Ома в комплексной форме. Существуют следующие основные формы представления: Тригонометрическая форма:  Недостаток – трудно производить математические операции с несколькими синусоидами. Графическая форма(волновая диаграмма).  Недостаток – трудность точного изображения и большие погрешности при расчетах с помощью графических построений. Векторы на плоскости в Декартовой системе координат. Длина вектора – амплитуда. Угол – начальная фаза.  Векторная диаграмма– это совокупность векторов, изображающих векторы тока, напряжения и э.д.с. цепи, исходящих из одной точки Недостаток: можно легко складывать и вычитать, трудно умножать и делить. 4. Комплексная форма представления.   Для анализа электрических цепей синусоидального тока удобнее применять закон Ома в комплексной форме. В отличие от обычной формы закона Ома, в комплексной форме напряжение, токи, сопротивления и ЭДС записываются как комплексные числа. Данное нововведение основано на том, что в цепях переменного тока существуют активные и реактивные значения напряжений, токов и сопротивлений, что требует определенных корректив.  Приемники R, L, C, в цепи переменного тока. Рассмотрим цепь переменного тока, содержащую индуктивность, ёмкость и резистор, соединённые последовательно. 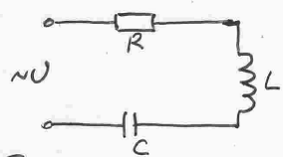 Через все эти элементы протекает один и тот же ток, поэтому в качестве основного выберем вектор тока, и будем строить вектор напряжения, приложенного к этой цепи. U = UL + Uc + UR Мы знаем, что напряжение на резисторе совпадает по фазе с током, напряжение на катушке опережает ток по фазе на 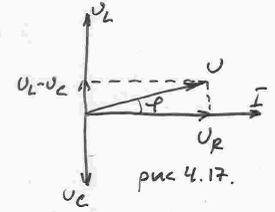 , а напряжение на ёмкости отстаёт от тока по фазе на . Запишем эти напряжения в следующем виде:UR = UmR∙sinωt = ImR∙sinωt UL = UmL∙sin(ωt + π/2) = Im∙ω∙L∙sin(ωt + π/2) (4.35) Uc = Umc∙sin(ωt – π/2) = (Im/ωC)∙sin(ωt – π/2) Построим векторную диаграмму и найдём вектор U. Из этой диаграммы находим модуль вектора приложенного к цепи напряжения и сдвиг фаз φ между током и напряжением: U =  = I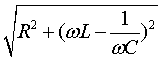Z гдеZ =  называется полным сопротивлением цепи. Из векторной диаграммы tgφ = (UL – Uc)/UR = 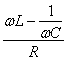 Разность фаз между током и напряжением определяется соотношением векторов UL, Uc и UR. При UL – Uc > 0 угол φ положительный и нагрузка имеет индуктивный характер. При UL меньше Uc угол отрицательный и нагрузка имеет емкостной характер. (См. рис.4.18.) А при UL = Uc нагрузка имеет активный характер. 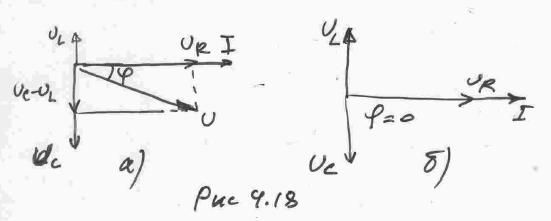 Разделив стороны треугольника напряжений (рис. 4.17) на значение тока в цепи, получим треугольник сопротивлений, в котором R – активное сопротивление, Z – полное сопротивление, а X = XL – Xc – реактивное сопротивление.  Рис.4.19. Кроме того, R = Z∙cosφ; X = Z∙sinφ (4.39). Когда напряжения на индуктивности и ёмкости, взаимно сдвинутые по фазе на 180 градусов, равны по величине, то они полностью компенсируют друг друга (рис.4.18б). Напряжение, приложенное к цепи, равно напряжению на активном сопротивлении, а ток в цепи совпадает по фазе с напряжением.Этот случай называется резонансом напряжений. Резонансные явления в электрических цепях. Резонансом напряжений в электрических цепях называется режим участка электрической цепи, содержащей индуктивный и емкостной элементы, при котором разность фаз между напряжением и током равна нулю  . Режим резонанса может быть получен при изменении частоты  питающего напряжения или изменением параметров элементов L и С. При последовательном соединении возникает резонанс напряжения.  . +Резонанс токов. При параллельном соединении конденсатора и соленоида (смотри рисунок), так же как и при последовательном, сила тока в цепи зависит от значений емкости и индуктивности. При изменении емкости и индуктивности при определенном их соотношении сила тока в неразветвленном участке цепи оказывается минимальной (практически близкой к нулю). При определенной частоте, называемой резонансной, реактивные составляющие проводимости могут сравняться по модулю и суммарная проводимость будет минимальной. Общее сопротивление при этом становится максимальным, общий ток минимальным, вектор тока совпадает с вектором напряжения.Такое явление называется резонансом токов. Мощность в цепи переменного тока. Коэффициент мощности. Способы повышения коэффициента мощности.  Коэффициент мощности 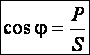 показывает, насколько рационально используется электрическая энергия. Чем ближе  , тем лучше, так как больше удельный вес Р в S, а именно активная мощность Р и совершает полезную работу.Для повышения  существует два способа:1. Естественный способ. Для повышения можно использовать потребители, которые не используют реактивную мощность (машины постоянного тока); асинхронные двигатели, соответствующие требуемой мощности, или специальные электрические машины (синхронные компенсаторы).2. Искусственный способ (рис. 1.21). Для повышения нужно уменьшить угол сдвига фаз между током и напряжением либо к нагрузке, носящей активно-индуктивный характер, параллельно подключить батарею емкостей. Для цепи, показанной на рис. 1.21, а, имеем  ,  .Так как  , то  . |