Линии второго порядка. Элементы аналитической геометрии
 Скачать 289 Kb. Скачать 289 Kb.
|
|
Тема: Элементы аналитической геометрии Количество учебных часов – 3 часа Актуальность темы (мотивация). Знание фундаментальных основ аналитической геометрии способствует формированию специализированных знаний, соединяющих профессиональные знания и умения узких специалистов и широкие общенаучные фундаментальные знания. Геометрический анализ живых форм представляет общий научный интерес. Применением геометрии в медицине является приравнивание природных тел к геометрическим, что позволяет произвести оценку и выносить количественные суждения. Линии, плоскости и поверхности используются при описании форм молекулярных связей, пространственных моделей ДНК, мембранных структур, а также различных их трансформаций, как в норме, так и при патологии. Несложные геометрические соображения должен иметь в виду специалист в области пластической хирургии, собирающийся компенсировать дефект при помощи пересадки или трансплантанта. 4. Цель занятия. Обучения студентов основным понятиям аналитической геометрии. Студент должен знать: Эллипс. Определение и каноническое уравнение. Гипербола. Определение и каноническое уравнение. Парабола. Определение и каноническое уравнение. Студент должен уметь: Исследовать форму эллипса. Исследовать форму гиперболы. Исследовать форму параболы. 5.Вопросы для самоподготовки. а) по базисным знаниям: Квадрат суммы и разности двух чисел. б) по теме занятия: Дайте определение эллипса и напишите его каноническое уравнение. Дайте определение гиперболы и напишите её каноническое уравнение. 3. Дайте определение параболы и напишите её каноническое уравнение. 6. Информационно-дидактический блок (аннотация, пособия): Краткая аннотация по теме: Исследование формы эллипса, гиперболы, параболы. Краткая теория§1.Эллипс Эллипсом называется геометрическое место точек, сумма расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (эта постоянная фокусами).    y y     M MrrrrYrry ii    fffffffff   Рис.1 Ч  тобы составить уравнение эллипса, примем за ось абсцисс прямую, соединяющую две данные точки F1 и F2 , выбрав на ней положительное направление от F2 и F1; начало координат возьмем в середине отрезка, соединяющего две данные точки (рис.1). Обозначим через 2 с расстояние F1 F2 между фокусами. Тогда координаты точек F1 и F2 будет соответственно (с;0) и (-с;0). Обозначая через х и у координаты произвольной точки М эллипса, выразим длины отрезков F1М и F2М по формуле расстояния между двумя точками: тобы составить уравнение эллипса, примем за ось абсцисс прямую, соединяющую две данные точки F1 и F2 , выбрав на ней положительное направление от F2 и F1; начало координат возьмем в середине отрезка, соединяющего две данные точки (рис.1). Обозначим через 2 с расстояние F1 F2 между фокусами. Тогда координаты точек F1 и F2 будет соответственно (с;0) и (-с;0). Обозначая через х и у координаты произвольной точки М эллипса, выразим длины отрезков F1М и F2М по формуле расстояния между двумя точками: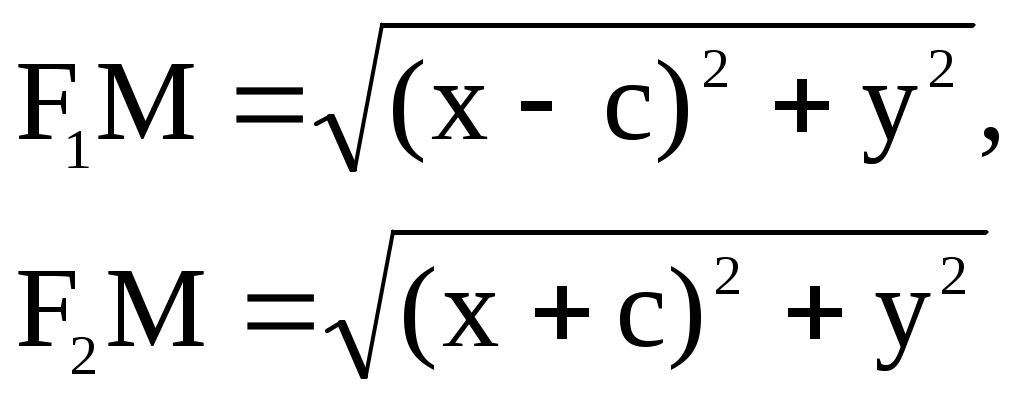 По определению эллипса сумма F1М+ F2М=2а, или Это есть уравнение эллипса в выбранной системе координат. Чтобы найденное уравнение эллипса приняло простейший вид, нужно в этом уравнении освободиться от радикалов. Перенося один радикал направо, получим; Возводя в квадрат обе части, найдем; или т.е. Возводя снова в квадрат, получим: или т.е. Разделив обе части на Так как по условию где положено Уравнение (2) называется каноническим уравнением эллипса. Форма эллипса (мера его сжатия) характеризуется его эксцентриситетом Расстояния некоторой точки эллипса М от его фокусов называются фокальными радиусами-векторами этой точки. Их обычно обозначают r1 и r2 (в силу определения эллипса для любой его точки В частном случае, когда а=в (с=0, е=0, фокусы сливаются в одной точке-центре), эллипс превращается в окружность (с уравнением Взаимное расположение точки 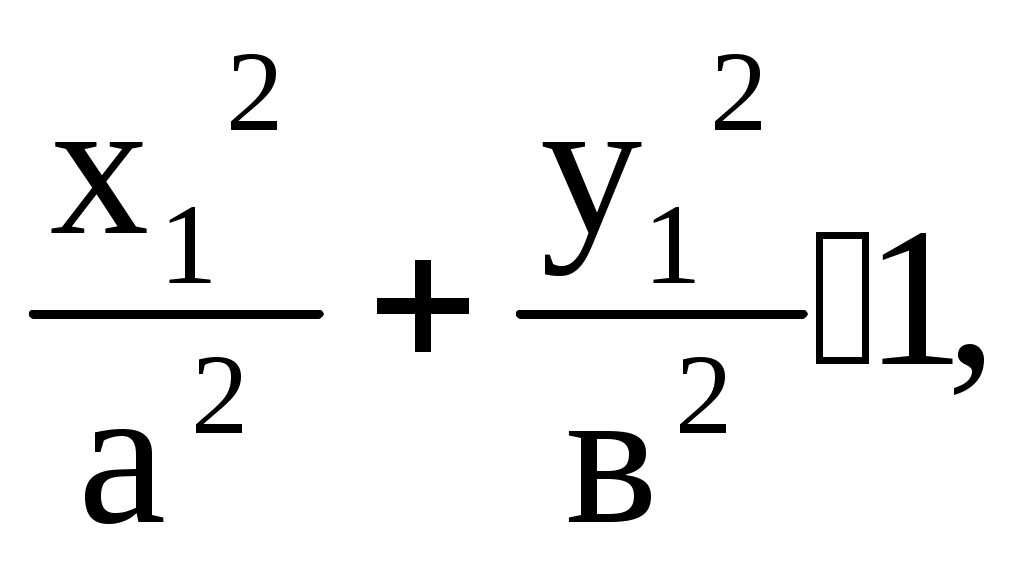 то точка М лежит вне эллипса; если то точка М лежит вне эллипса; если 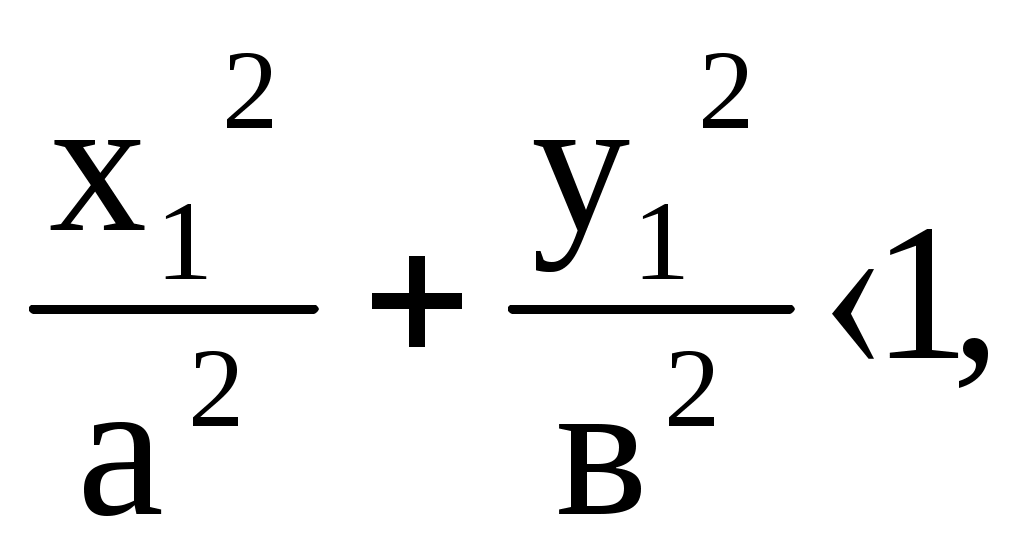 то точка М лежит внутри эллипса. то точка М лежит внутри эллипса.Фокальные радиусы-векторы выражаются через абсциссу точки эллипса по формулам Пример 1. Составить каноническое уравнение эллипса, проходящего через точки Решение: Пусть Отсюда находим а2=10, в2=1. Итак, уравнение эллипса имеет вид Две прямые Пример 2: Найти эксцентриситет и директрисы эллипса х2+2у2=2. Написав уравнение эллипса в виде: заключаем, что а2=2, в2=1. Следовательно, с2=а2-в2=2-1=1, откуда Директрисы проходят на расстоянии §2. Гипербола и ее асимптоты. Гиперболой называется геометрическое место точек, разность расстояний которых до двух данных точек, называемых фокусами, есть величина постоянная (эта постоянная должна быть положительной и меньше расстояния между фокусами). Обозначим эту постоянную через 2а, расстояние между фокусами через 2с. Пусть          Р  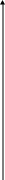   ис. 2. По определению гиперболы В правой части равенства нужно выбрать знак плюс, если 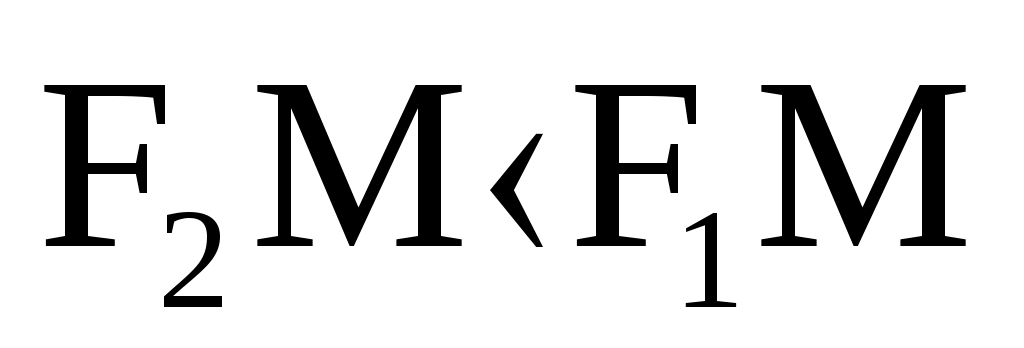 . .Так как, Это и есть уравнение гиперболы в выбранной системе координат. Освобождаясь в этом уравнении от радикалов, можно привести уравнение к простейшему виду. Перенося первый радикал в правую часть равенства и возводя обе части в квадрат, после очевидных преобразований получим: Возведя еще раз обе части равенства квадрат, сделав приведение подобных членов и разделив на свободный член, получим: Так как получим каноническое уравнение гиперболы: Гипербола состоит из двух ветвей и расположена симметрично относительно осей координат. Точки А1(а;0) и А2(-а,0) называются вершинами гиперболы. Отрезок Прямая называется асимптотой гиперболы, если расстояние точки М(х, у) гиперболы от этой прямой стремится к нулю при Для построения асимптот гиперболы строят осевой прямоугольник гиперболы со сторонами х=а, х=-а, у=в, у=-в. Прямые, проходящие через противоположные вершины этого прямоугольника, являются асимптотами гиперболы. На рис. 2. указано взаимное расположение гиперболы и ее асимптот. Отношение Фокальные радиусы-векторы правой ветви гиперболы: Фокальные радиусы-векторы левой ветви гиперболы: Если а=в, то уравнение гиперболы принимает вид Такая гипербола называется равнобочной. Ее асимптоты образуют прямой угол. Если за оси координат принять асимптоты равнобочной гиперболы, то ее уравнение примет вид Уравнение Две гиперболы имеют одни и те же полуоси и одни и те же асимптоты, но действительная ось одной служит мнимой осью другой, и наоборот. Такие две гиперболы называются сопряженными. Пример 1: На правой ветви гиперболы найти точку, расстояние которой от правого фокуса в два раза меньше ее расстояния от левого фокуса. Решение: Для правой ветви гиперболы фокальные радиусы-векторы определяются по формулам Ординату находим из гиперболы: Таким образом, условию задачи удовлетворяют две точки: Пример 2: Эксцентриситет гиперболы равен Решение: Согласно определению эксцентриситета, имеем Другое равенство получим из условия нахождения точки М на гиперболе, т.е. Поскольку Таким образом, уравнение искомой гиперболы имеет вид §3. Парабола. Парабола есть геометрическое место точек, равноотстоящих от данной точки, называемой фокусом, и данной прямой, называемой директрисой (предполагается, что данная точка не лежит на прямой).      Рис. 3. Чтобы составить уравнение параболы, примем за ось ох прямую, проходящую через фокус F перпендикулярно к директрисе, и будем считать ее направленной от директрисы к фокусу; за начало координат возьмем середину 0 отрезка от точки F до данной прямой, длину которого обозначим через р (Рис. 3.). Величину р называют параметром параболы. Координаты фокуса F будут Чтобы придать ему простейший вид, возведем обе части в квадрат. Будем иметь: или откуда Полученное уравнение называется каноническим уравнением параболы. Эта парабола расположена симметрично относительно оси абсцисс (р>0). Уравнение х2=2ру (2) является уравнением параболы, симметричной относительно оси ординат. При р>0 параболы (1) и (2) обращены в положительную сторону соответствующей оси, а при р<0 – в отрицательную сторону. Длина фокального радиуса-вектора параболы у2=2ру определяется по формуле Обозначая через r расстояние любой точки М параболы до фокуса, а через d ее расстояние до директрисы, мы имеем r =d, или        Поэтому эксцентриситет параболы принимают равным единице. Уравнение директрисы параболы будет:    Рис. 4. Пример 1. Составить уравнение параболы, симметричной относительно оси ох, с вершиной в начале координат, если длина некоторой хорды этой параболы, перпендикулярной оси ох, равна 16, а расстояние этой хорды от вершины равно 6. Решение: Так как известны длины хорды и расстояние ее от вершины, то, следовательно, известны координаты конца этой хорды-точки М, лежащей на параболе. Уравнение параболы имеет вид у2=2рх; полагая в нем х=6, у=8, находим 82 =2р·6, откуда Пример2: Составить уравнение параболы с вершиной в начале координат, симметричной относительно оси оу и отсекающей на биссектрисе I и III координатных углов хорду длиной Решение: Искомое уравнение параболы х2=2ру, уравнение биссектрисы у-х. Таким образом, получаем точки пересечения параболы с биссектрисой: О(0,0) и М(2р,2р). Длина хорды определяется как расстояние между двумя точками: 7. Содержание занятия Самостоятельная работа студентов. Построить эллипс Написать каноническое уравнение эллипса, если известно, что: 1) расстояние между фокусами равно 8, а малая полуось b=3; 2) большая полуось a=6, а эксцентриситет Написать каноническое уравнение эллипса, проходящего через точки: 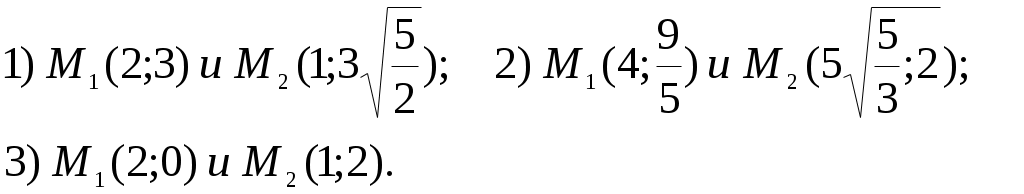 Эллипс проходит через точки Построить гиперболу Построить гиперболу На гиперболе Гипербола проходит через точку Построить параболу Написать уравнение параболы: 1) проходящей через точки (0;0) и (1;-3) и симметричной относительно оси Написать уравнение окружности, имеющей центр в фокусе параболы Написать уравнение параболы и директрисы, если известно, что парабола симметрична относительно оси Составить канонические уравнения прямой, проходящей через две данные точки: 1) (1;- Совместная работа студентов с преподавателем. Преподаватель проводит проверку самостоятельной работы студентов с опросом по теме каждого студента. Обобщает результаты индивидуальной работы, останавливаясь на основных ошибках. Устраняет пробелы в знаниях по теме. Контроль исходного и заключительного уровня знаний. Анализ и итог практического занятия по результатам устных вопросов темы, а также индивидуальных работ студентов. 8. Литература. Шипачев В.С. «Сборник задач по высшей математике», Москва, «Высшая школа», 2000 г Привалов И.И. Аналитическая геометрия, Москва, «Наука», 1966 г. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. Москва, «Высшая школа». Беклемишев Д.В. Курс аналитической геометрии. Москва, «Наука», 1974 г. Лихолетов И.И., Моцкевич И.П. Руководство к решению задач. Минск, «Высшая школа», 1966 г. Погорелов А.В. Аналитическая геометрия. Москва, «Наука», 1978 г. |
