вкр. Лекция. Основы финансовых расчетов. Элементы финансовой математики
 Скачать 171.08 Kb. Скачать 171.08 Kb.
|
|
Элементы финансовой математики Разработка многих разделов бизнес-плана невозможно без элементарных знаний финансовой математики. В широком смысле финансовая математика — это любые финансовые вычисления для достижения какой-либо цели. К основным понятиям финансовой математики относятся: I - проценты — доход от предоставления капитала в долг. P – первоначальная инвестированная сумма. S - наращенная сумма, S = Р + I. M – множитель наращения, S = P*M n - период начисления — промежуток времени, за который начисляются проценты, измеряется в годах. m - количество интервалов начисления в каждом году - минимальный промежуток времени, по прошествии которого происходит начисление процентов. Процентная ставка — величина, которая характеризует интенсивность начисления процентов, имеет различные обозначения. Ставки всегда годовые. Различают два способа начисления процентов: декурсивный и антисипативный. При декурсивном способе проценты начисляются в конце каждого интервала начисления. Декурсивная процентная ставка i называется ссудной. При антисипативном (предварительном) способе проценты начисляются в начале каждого интервала начисления. Антисипативная процентная ставка d называется учетной ставкой. В обоих способах начисления процентов процентные ставки могут быть простыми (в течение всего периода начисления применяются к первоначальной сумме), либо сложными (в каждом интервале начисления применяются к текущей наращенной сумме). Простые ставки используются в краткосрочных операциях до года, сложные – в средне и долгосрочных. Простые ссудные ставки. Для начала рассмотрим простые ссудные проценты, для которых в течение всего периода наращение применяется к первоначальной сумме. Предположим, что первоначальная сумма Р была помещена в банк под iпроцентов годовых (проценты простые). По прошествии 1 года наращенная сумма S = Р (первоначальная сумма) + iP(проценты) = Р(1 + i). По прошествии еще 1 года (всего 2х лет) наращенная сумма S = Р(1 + i) (наращенная сумма после одного года) + iP(проценты) = Р(1 + 2i). По прошествии еще 1 года (всего 3х лет) наращенная сумма S= Р(1 + 2i) (наращенная сумма после двух лет) + iP(проценты) = Р(1 + 3i). Если п — период начисления процентов (в годах), то наращенная сумма через п лет: S = Р(1 + ni) Математическим дисконтированием называется операция, когда по наращенной сумме S, периоду начисления n и простой процентной ставке i определяют первоначальную сумму Р: Р =S/(1+ni) В формуле (1) период начисления n измеряется в годах. Это не всегда удобно, когда период начисления меньше года, поэтому полагают n = t/T, где t— период начисления (в днях), T— продолжительность года (в днях), тогда S= Р(1 + it/T) Дата выдачи и дата погашения ссуды всегда считаются за один день. В немецкой практике начисления процентов один полный месяц равен 30 дням, продолжительность года T = 360 дней. Такие проценты носят наименование обыкновенные проценты с приближенным числом дней ссуды, обозначается 360/360. Во французской практике период начисления процентов равен фактическому сроку, продолжительность года T = 360 дней, называются обыкновенные проценты с точным числом дней ссуды, обозначаются 365/360. В английской практике период начисления процентов равен фактическому сроку, продолжительность года T= 365 дней (невисокосный год) или 366 дней (високосный год), называются точные проценты с точным числом дней ссуды, обозначаются 365/365. Пример. Первоначальная сумма 3000 руб. помещена в банк под 12% годовых, проценты простые ссудные, на срок с 22 мая по 24 декабря того же года. Определить наращенную сумму в каждой из практик начисления процентов. Дано: Р = 3000 руб. i = 12% t: 22.05 – 24.12 Найти: S = ? Решение: В немецкой практике начисления процентов продолжительность года T = 360 дней, t = 10 (май) + 6*30 (июнь, июль, август, сентябрь, октябрь, ноябрь) + 24 (декабрь) - 1 (день открытия и день закрытия счета считаются за один день) = 213 дней. Тогда S= Р(1 + it/Т) = 3000*(1 + 0,12*213/360) = 3213 руб. Во французской практике продолжительность года Т = 360 дней, t= 10 (май) + 30 (июнь) + 31 (июль) + 31 (август) + 30 (сентябрь) + 31 (октябрь) + 30 (ноябрь) +24 (декабрь) - 1 (день открытия и день закрытия счета считаются за один день) = 216 дней. Тогда S = Р(1 + it/Т) = 3000*(1 + 0,12*216/360) = 3216 руб. В английской практике продолжительность года Т = 365 дней,t = 216 дней. Тогда S= Р(1 + it/T) = 3000*(1 + 0,12*216/365) = 3213,04 руб. Погашение задолженности частями. Необходимым условием финансовой или кредитной операции в любой ее форме является сбалансированность вложений и отдачи. Понятие сбалансированности удобно пояснить на графике (рис.1).     R3 R2 R1 P                 T t3 t2 t1  Актуарный метод                  R1 R2 I1 I2         R3 S1 S2   K2 K1          T t3 t2 t1 Правило торговца     R3      S Q1+Q2  Q2          t3 R1 R2 Q1        t1 t2 T Рис.1. Погашение задолженности частями Пусть выдан кредит на срок n в размере Р. На протяжении этого срока в счет погашения задолженности производятся два платежа R1 и R2, а в конце срока выплачивается остаток задолженности в сумме R3 (не имеет значения, какая часть этой суммы идет на выплату процентов, а какая — на погашение долга). Очевидно, что на интервале t1задолженность возрастает (в силу начисления процентов) до величины S1. В конце этого периода выплачивается в счет погашения задолженности сумма R1, долг уменьшается до К1 и т.д. Заканчивается операция получением кредитором в окончательный расчет суммы R3. В этот момент задолженность должна быть равна нулю. Назовем такой график контуром операции. Сбалансированная операция обязательно имеет замкнутый контур. Иначе говоря, последняя выплата полностью покрывает остаток задолженности. В этом случае совокупность платежей точно соответствует условиям сделки. Краткосрочные обязательства иногда погашаются с помощью ряда промежуточных платежей. В этом случае надо решить вопрос о том, какую сумму надо брать за базу для расчета процентов и каким путем определять остаток задолженности. Существуют два метода решения этой задачи. Первый, который применяется в основном в операциях со сроком более года, называют актуарным методом. Второй метод назван правилом торговца. Он используется коммерческими фирмами в сделках со сроком не более года. Если иное не оговорено, то при начислении процентов в обоих методах используются обыкновенные проценты с приближенным числом дней займа (360/360). Актуарный метод предполагает последовательное начисление процентов на фактические суммы долга. Частичный платеж идет в первую очередь на погашение процентов, начисленных на дату платежа. Если величина платежа превышает сумму начисленных процентов, то разница (остаток) идет на погашение основной суммы долга. Непогашенный остаток долга служит базой для начисления процентов за следующий период и т.д. Если же частичный платеж меньше начисленных процентов, то никакие зачеты в сумме долга не делаются. Поступление приплюсовывается к следующему платежу. Для случая, показанного на рис. 1, получим следующие расчетные формулы для определения остатка задолженности К1 = Р(1 + t1i) – R1, если I1 ≤ R1 K2 = K1(1 + t2i) – R2, если I2 ≤ R2 Задолженность на конец срока должна быть полностью погашена, поэтому: K2(1 + t3i) – R3 = 0 Иной подход предусматривается правилом торговца. Здесь возможны два варианта. Если срок ссуды не превышает год, то сумма долга с процентами остается неизменной до полного погашения. В свою очередь накапливаются частичные платежи с начисленными на них до конца срока процентами. Последний взнос должен быть равен разности этих сумм. В случае, когда срок превышает год, указанные выше расчеты делаются для годового периода задолженности. В конце года из суммы задолженности вычитается наращенная сумма накопленных частичных платежей. Остаток погашается в следующем году. Алгоритм можно записать следующим образом: 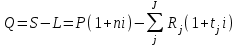 , , где Q — остаток долга на конец срока или года, S — наращенная сумма долга, L — наращенная сумма платежей, R — сумма частичного платежа, J — общий срок ссуды, tj — интервал времени от момента платежа до конца срока ссуды или года. Графическое изображение такой операции при выплате двух промежуточных платежей охватывает два параллельных контура. Первый характеризует наращение задолженности, второй — наращение на суммы поступлений. Заметим, что для одних и тех же данных актуарный метод и правило торговца в общем случае дают разные результаты. Остаток задолженности по первому методу немного выше, чем по второму. Пример 8. Обязательство 1,5 млн.руб., датированное 10 августа текущего года, должно быть погашено 10 июня следующего года. Ссуда выдана под 20% годовых. В счет погашения долга 10 декабря текущего года поступило 800 тыс.руб. Определить погасительный платеж. Дано: Р = 1,5 млн.руб. i = 20% R1 = 0,8 млн.руб. t1 = 4 мес. (с 10.08 по 10.12) Найти: Q = ? Решение: остаток долга на конец срока составит Q= 1,5*(1 + 10*0,2/12) - 0,8*(1 + 6*0,2/12) = 0,87 млн.руб. В свою очередь, при применении актуарного метода получим Q = [(1,5 + 4*0,2/12) - 0,8]*(1 + 6*0,2/12) = 0,88 млн.руб. Сложные ссудные проценты В случае сложных процентов, в конце каждого интервала начисления процентная ставка применяется к наращенной сумме на начало этого интервала начисления. Предположим, что первоначальная сумма Р была помещена в банк под i процентов годовых (проценты сложные ссудные). По прошествии первого года наращенная сумма S= Р (сумма на начало этого интервала начисления) + iP (проценты) = Р(1 + i). По прошествии второго года наращенная сумма после двух лет S= Р(1 + i) (наращенная сумма после одного года) + iP(1+i) (проценты) = Р(1 + i)(1 + i) = P(1+i)2. По прошествии третьего года наращенная сумма S= Р(1 + i)2 (наращенная сумма после двух лет) + iP(1+ i)2 (проценты) = Р(1+i)(1+i)2 = Р(1 + i)3. Если n — период начисления процентов (в годах), то наращенная сумма через n лет: S= Р(1 + i)n Математическим дисконтированием называется операция, когда по наращенной сумме S, периоду начисления n и сложной процентной ставке i нужно определить первоначальную сумму Р: Р = S/(1 + i)n Сложная номинальная ставка. Начисление сложных процентов может происходить несколько раз в году. В этом случае указывают номинальную процентную ставку j, на основании которой рассчитывают процентную ставку для каждого интервала начисления. Если в году m интервалов начисления, то на каждом из них процентная ставка равна j/m. Тогда наращенная сумма S= Р(1 + j/m)nm Антисипативные ставки (простая и сложная) Рассмотрим антисипативный способ начисления простых процентов. Сумма получаемого дохода рассчитывается исходя из наращенной суммы S. S - это величина погашаемого кредита. Заемщик получает в начале периода начисления процентов сумму Р = S - D, где D - это дисконт (разность между размером кредита S и непосредственно выданной суммой Р). Такая операция называется дисконтированием по простой учетной ставке. На практике учетные ставки применяются при учете (покупке) векселей. Пустьd — простая учетная ставка,п — период начисления процентов (в годах). Тогда D = ndS и Р=S - D = S - ndS => P = S(1 - nd) Если период начисления меньше года, то полагают n = t/T, где T — продолжительность года (в днях), t — период начисления (в днях). Тогда Р = S(1 – td/T). Если d — сложная учетная ставка, n — период начисления процентов (в годах). Тогда D = ndS и Р=S - D = S - ndS P = S(1 -d)n Экивалентность ставок. Очень часто перед инвестором стоит задача выбора одного из этих вариантов инвестирования первоначальной суммы. Возникает задача сравнения между собой различных процентных ставок. Две ставки называются эквивалентными, если при одинаковой первоначальной сумме Р и на одинаковом периоде начисления п они приводят к одинаковой наращенной сумме S. При сравнении двух ставок из разных классов для одной из них находят эквивалентную ей ставку из другого класса и проводят сравнение двух ставок из одного класса. Для примера определим формулу эквивалентности простой ссудной процентной ставки и сложной ссудной процентной ставки. Пусть Р — первоначальная сумма, п — период начисления. При использовании простой процентной ставки i наращенная сумма S1= Р(1 + ni). При использовании сложной процентной ставки iC наращенная сумма S2 = Р(1 + iс)n Так как ставки эквивалентны, то наращенные суммы равны: S1 = S2, то есть Р(1 + ni) = Р(1 + iс)n. Следовательно 1 + ni = (1 + iс)n => i = ((1 + iс)n -1)/n Эквивалентность платежей. На практике часто возникают случаи, когда необходимо заменить одно денежное обязательство другим, например, с более отдаленным сроком платежа, объединить несколько платежей в один (консолидировать платежи) и т.п. Такие изменения не могут быть произвольными. Неизбежно возникает вопрос о принципе, на котором должны базироваться изменения условий контрактов. Таким общепринятым принципом является финансовая эквивалентность обязательств. Эквивалентными считаются такие платежи, которые, будучи “приведенными” к одному моменту времени, оказываются равными. Приведение осуществляется путем дисконтирования (приведение к более ранней дате) или, наоборот, наращения суммы платежа (если эта дата относится к будущему). Если при изменении условий контракта принцип финансовой эквивалентности не соблюдается, то одна из участвующих сторон терпит ущерб, размер которого можно заранее определить. Общий метод решения задач при различных изменениях условий выплат денежных сумм заключается в разработке так называемого уравнения эквивалентности, в котором сумма заменяемых платежей, приведенных к какому-либо моменту времени, приравнивается к сумме платежей по новому обязательству, приведенных к той же дате. Для краткосрочных обязательств приведение осуществляется обычно на основе простых ставок, для средне- и долгосрочных - с помощью сложных процентных ставок. В простых случаях часто можно обойтись без разработки и решения уравнения эквивалентности. При построении уравнения эквивалентности каждый платеж можно рассматривать и как первоначальную сумму, которую необходимо наращивать к определенному более позднему моменту времени, и как наращенную сумму, которую будем дисконтировать, приводя ее к более ранней дате. Поэтому целесообразно обозначать каждый платеж переменной D. Одним из распространенных случаев изменения условий контрактов является консолидация (объединение) платежей. Пусть платежи D1, D2,..., Dm со сроками n1, n2,…,nmзаменяются одним в сумме D0 и сроком n0. В этом случае возможны две постановки задачи: если задается срок n0, то находится сумма D0 и наоборот, если задана сумма консолидированного платежа D0, то определяется срок n0. Рассмотрим обе постановки задачи. При решении задачи определения размера консолидированного платежа уравнение эквивалентности имеет простой вид. В общем случае, когда n1 При применении простых процентных ставок 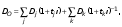 где Dj – размеры объединяемых платежей со сроками nj < n0, Dk – размеры объединяемых платежей со сроками nk > n0; tj = n0 – nj, tk = nk – n0. Консолидацию платежей можно осуществить и на основе сложных процентных ставок. Для общего случая (n1< n0< nm) получим 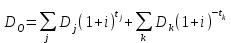 Если при объединении платежей задана величина консолидированного платежа, то возникает проблема определения его срока n0. В этом случае уравнение эквивалентности удобно представить в виде равенства современных стоимостей соответствующих платежей. При применении простой ссудной ставки это равенство имеет вид 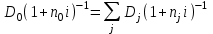 , следовательно: , следовательно: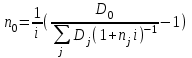 Определим срок консолидированного платежа, если проценты сложные. Уравнение эквивалентности будет выглядеть следующим образом 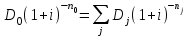 . .Для упрощения дальнейшей записи пусть 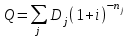 , тогда , тогда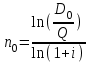 (31) (31)Учет инфляции Влияние инфляции на финансовые операции удобно показать, если ввести следующие обозначения. Пусть S — это сумма денег, для которой рассматривается покупательная способность при отсутствии инфляции. Sα — это сумма денег, покупательная способность которой с учетом инфляции равна покупательной способности суммы S при отсутствии инфляции, то есть один и тот же набор товаров можно купить на суммы S (при отсутствии инфляции) и Sα (с учетом инфляции). Понятно, что Sα > S. Обозначим ΔS = Sα - S. Тогда величина α = ΔS/S = (Sα - S)/S называется уровнем (темпом) инфляции. Это индекс прироста. Он показывает, на сколько процентов в среднем выросли цены за рассматриваемый период. ΔS = Sα - S => Sα = S + ΔS. Ho α = ΔS/S => ΔS = αS. Тогда Sα = S + ΔS = S + αS = S(1 + α). Величину Iи = 1 + α называют индексом инфляции. Это индекс роста. Он показывает, во сколько раз в среднем выросли цены за рассматриваемый период. Рассмотрим расчет ставки, учитывающей инфляцию, для случая простых процентов. Пусть Р — первоначальная сумма, n — период начисления, i — годовая простая ставка ссудного процента. Наращенная сумма для простых процентов S = Р(1 + ni). Эта сумма не учитывает инфляцию. Пусть уровень инфляции за рассматриваемый период п равен α. Sα — это сумма денег, покупательная способность которой с учетом инфляции равна покупательной способности суммы S при отсутствии инфляции. Тогда Sα = S(1 + α) = Р(1 + ni)(1 + α) Но сумму Sα можно получить, поместив первоначальную сумму Р на срок п под простую ставку ссудных процентов iα, учитывающую инфляцию: Sα = Р(1 + niα) Следовательно, Р(1 + ni)(1 + α) = Р(1 + niα) => (1 + ni)(1 + α) = (1 + niα) => 1 + ni + α + αni = 1 + niα => iα = (ni + α + αni)/n Именно под такую простую ставку ссудных процентов нужно положить первоначальную сумму на срок n, чтобы при уровне инфляции α за рассматриваемый период обеспечить реальную доходность в виде годовой простой ставки ссудных процентов i. Если n = 1 год, то iα = i + α + αi. Это формула Фишера, а величина α + αi называется инфляционной премией. ni + α + αni = niα => Формула реальной доходности в виде годовой простой ставки ссудных процентов для случая, когда первоначальная сумма была инвестирована под простую ставку ссудных процентов iα на срок n при уровне инфляции α за рассматриваемый период: i = (niα – α)/(n + αn) Рассмотрим расчет ставки, учитывающей инфляцию, для случая сложных процентов. Пусть Р — первоначальная сумма, п — период начисления, i — годовая сложная ставка ссудного процента. Тогда наращенная сумма S = Р(1 + i)n. Эта сумма не учитывает инфляцию. Пусть уровень инфляции за рассматриваемый период п равен α. Sα— это сумма денег, покупательная способность которой с учетом инфляции равна покупательной способности суммы S при отсутствии инфляции. Тогда Sα = S(1 + α) = Р(1 + i)n (1 + α) Но сумму Sα можно получить, поместив первоначальную сумму Р на срок п под сложную ставку ссудных процентов iα, учитывающую инфляцию: Sα = Р(1 + iα)n Следовательно, Р(1 + i)n(1 + α) = Р(1 + iα)n => (1 + i)n(1 + α) = (1 + iα)n=> 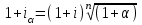 => =>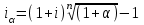 Именно под такую сложную ставку ссудных процентов нужно положить первоначальную сумму на срок n, чтобы при уровне инфляции α за рассматриваемый период обеспечить реальную доходность в виде годовой сложной ставки ссудных процентов i. (1 + i)n(1 + α) = (1 + iα)n => Формула реальной доходности в виде годовой сложной ставки ссудных процентов для случая, когда первоначальная сумма была инвестирована под сложную ставку ссудных процентов iα на срок п при уровне инфляции α за рассматриваемый период: 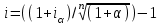 |
