что то. тема 6. Элементы кристаллографии. Основные законы кристаллографии
 Скачать 220.96 Kb. Скачать 220.96 Kb.
|
|
Элементы кристаллографии. Основные законы кристаллографии. В кристалле структурные элементы (ионы, атомные остовы, молекулы), образующие кристалл, располагаются закономерно по разным направлениям (рис. 4.6, а). Обычно пространственное изображение структуры кристаллов представляют схематично (рис. 4.6, б), отмечая точками центры тяжести структурных элементов, включая характеристики решетки.  Рис. 4.6. Расположение элементов в кристалле: а — изображение с размещением объема атомного остова элемента; б — пространственное изображение элементарной ячейки и ее параметры Первый закон кристаллографии – закон постоянства углов был сформулирован датским ученым Н. Стеноном на примере двух веществ – кварца и гематита. Он гласит: углы между соответственными гранями кристаллов данного вещества постоянны и характерны для этого вещества. Французский кристаллограф аббат Р.Ж. Гаюи нашел второй закон кристаллографии – закон рациональных параметров. Если в качестве трех координатных осей кристалла выбрать некоторые его ребра, то отрезки, отсекаемые гранями на осях кристалла, относятся как целые числа. Таким образом, эти отрезки могут быть выражены как кратные некоторых осевых единиц. Наличие таких осевых единиц в трех направлениях приводит к выводу о трехмерной микропериодичности строения кристаллов. Из закона рациональных параметров и представлений об атомизме с необходимостью вытекает утверждение о трехмерно-периодическом атомном строении кристаллов. Макроскопические и микроскопические характеристики кристаллов. Наиболее общими макроскопическими свойствами кристаллического вещества являются однородность, анизотропия и симметрия. Понятие макроскопической однородности означает, что в любых участках кристаллического вещества все свойства его тождественны. Не только кристаллы, но и жидкости, аморфные тела и газы обладают свойством макроскопической однородности. Специфичность кристаллического вещества и отличие его от других состояний проявляется при рассмотрении его анизотропии. С точки зрения симметрии, можно сформулировать понятие кристаллической однородности и анизотропии. Однородность – независимость свойств кристаллического вещества от выбора точки измерения – с позиций симметрии является инвариантностью по отношению к произвольному, параллельному себе его переносу. Анизотропия же кристаллов – зависимость свойств от направлений – сама проявляется в рамках симметрии: функции, описывающие свойства, сами являются симметричными. Таким образом, кристаллическое вещество по своим макроскопическим признакам можно определить как однородную анизотропную симметричную среду Решетка и структура кристаллов Конкретное расположение атомов в кристалле называют структурой вещества. Всякое кристаллическое вещество может быть разбито на тождественные участки (ячейки), содержащие один или несколько определенным образом расположенных в них атомов. Бесконечно протяженное расположение атомов, состоящее из периодически повторяющихся одинаковых ячеек, называют кристаллическим пространством. Математически кристаллическое пространство строят на следующих постулатах. 1. Не все точки кристаллического пространства одинаковы (в любом смысле). 2. Кристаллическое пространство однородно, т.е. существует шар такого постоянного радиуса R (шар однородности), что где бы его ни выбрать, внутри него найдется точка x ′, симметрично равная любой наперед заданной точке пространства x. 3. В пространстве есть такие точки (по крайней мере, одна точка x), что вокруг них в шаре радиуса r (шар дискретности) нет ни одной симметрично равной им точки. Указанные постулаты достаточны для построения всей геометрической кристаллографии и вывода многих геометрических свойств кристаллического вещества. Кристаллографические проекции. Внешняя огранка кристалла является характерным признаком данного вещества. На основании анализа углов между гранями можно определить принадлежность кристалла к тому или иному веществу. Для измерения углов между гранями применяют специальные оптические устройства, называемые гониометрами. Линейная проекция. Для построения линейной проекции используют прямой кристаллографический комплекс, центр которого C располагают на определенном расстоянии D от плоскости проекции P (рис. 1.4) 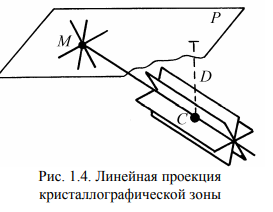 Гномоническая проекция отличается от линейной тем, что вместо прямого комплекса используется обратный. В этом случаеплоскости прямого комплекса изображаются на проекции точками, а прямые – линиями. Зона плоскостей проектируется рядом точек, расположенных на прямой, являющейся проекцией оси зоны (рис. 1.5) 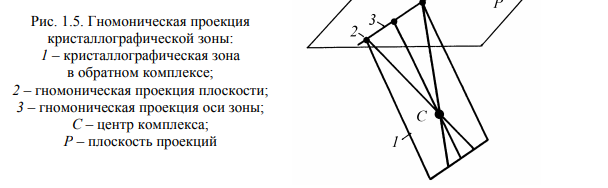 Сферическая проекция получается при проектировании компонентов прямого кристаллографического комплекса, помещенного в центр сферы произвольного радиуса, на сферическую поверхность. Гномосферическая проекция получается при проектировании на сферу компонентов обратного комплекса. В этом случае кристаллографическая зона проектируется рядом точек, расположенных на большом круге, являющемся проекцией оси зоны. Стереографическая проекция. При построении стереографической проекции центр кристаллографического комплекса C совмещается с центром сферы О (рис. 1.6). 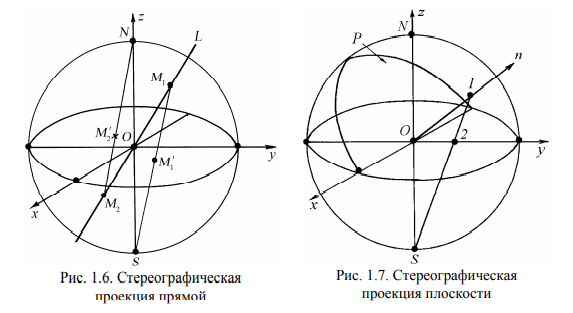 Гномостереографическая проекция (стереографическая проекция обратного комплекса) является более удобной для решения практических задач. На этой проекции плоскости изображаются точками, а прямые – большими кругами. 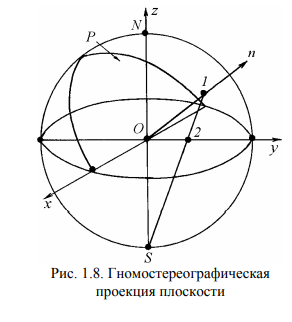 Пространственная решетка. Любой узел пространственной решетки определяется линейной формой: Rm = m1a1 + m2a2 + m3a3, (1.10) где a1, a2, a3 – векторы трансляций, а m1, m2, m3 – целые числа. Начало координат при этом может быть выбрано в любом узле пространственной решетки Пространственная решетка может быть получена бесконечным параллельным повторением параллелепипеда, построенного на векторах кратчайших трансляций (базисных векторах) a1, a2, a3. Такой параллелепипед называют элементарной ячейкой. Можно показать, что при сделанном выборе трансляций элементарная ячейка не содержит узлов, находящихся на ее гранях или внутри объема. Такую ячейку называют примитивной или простой. Длины векторов a1, a2, a3 и углы между ними α1, α2, α3 называют параметрами решетки, иногда их обозначают как a, b, c и α, β и γ соответственно. Для описания кристаллического вещества используют кристаллографическую систему координат с векторами трансляций a1, a2, a3 (a, b, c) В общем случае это шесть параметров: косоугольные координаты с неодинаковыми масштабными отрезками по осям: Элементарная ячейка a ≠ b ≠ c, α ≠ β ≠ γ ≠ 90о . 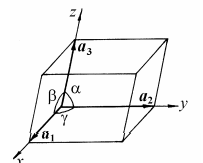 Кристаллографические символы Символы узла. Положение любого узла в пространственной решетке определяется вектором Rmnp Rmnp = ma + nb + p c. (1.16) Три целых числа m, n, p однозначно определяют положение узла и называются индексами данного узла. Совокупность чисел m, n, p, записанная в двойных квадратных скобках [[m1 m2 m3]], называется символом узла. Узлы, лежащие на одной прямой, имеют пропорциональные индексы. Символы узловой прямой. Решетку можно представить как семейство параллельных узловых прямых. Это семейство можно характеризовать прямой, проходящей через начало координат, которое принимается за первую точку, определяющую данную прямую. Второй определяющей точкой является ближайший узел с целочисленными координатами. Координаты этого узла, взятые в квадратные скобки, принимают за кристаллографический символ прямой [mnp]. Индексы важнейших направлений в кубическом кристалле приведены на рис. 1.27. Оси координат имеют символы: ox – [100], oy – [010], oz – [001]. Одно из основных преимуществ кристаллографической символики состоит в неизменности символов осей координат от сингонии кристалла. 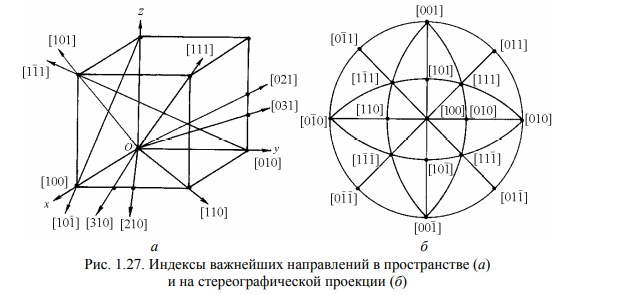 Индексы в угловых скобках используют для обозначения направлений определенного типа, связанных элементами симметрии. Например, для кубической сингонии символ обозначает направления [100], [010] и [001], а также [100], [010], [001], т.е. направления, индексы которых отличаются либо перестановкой, либо знаком. Символы плоскости. Пространственная решетка может быть представлена семейством параллельных узловых плоскостей. Пусть одна из таких плоскостей семейства отсекает на осях координат отрезки A, B, C. Уравнение такой плоскости в отрезках можно записать в виде (x/A) + (y/B) + (z/C) = 1. (1.18) Переменные x, y, z в этом уравнении являются координатами узлов пространственной решетки, лежащих в данной плоскости, поэтому они равны целому числу m, n, p трансляций по каждой из осей: x = m a; y = n b; z = p c. (1.19) Подставляя значения координат в уравнение (1.18), получаем m (a/A) + n (b/B) + p (c/C) = 1. (1.20) Так как правая часть уравнения (1.20) равна единице, то отношения a/A, b/B, c/C представляют собой рациональные числа. В этом случае отношение между ними всегда будет равно отношению трех простых (не имеющих общего множителя) целых чисел h, k, l: 1/(A/a) : 1/(B/b) : 1/(C/c) = h : k : l. |
