База_з_мед_фізики_Мат_стат_;_Диф. Елементи математичної статистики Випадкові величини х поділяються на
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
8. Для перевірки точності визначення білків плазми крові методом електрофорезу на папері було зроблено 8 послідовних аналізів крові однієї людини. Отримані дані про вміст β-глобулінів у плазмі (в %) 7,4; 7,6; 7,7; 7,8; 7,4; 8; 7,8; 7,5. Чому дорівнює точкова оцінка істинного вмісту β-глобуліну у плазмі крові? A) 7,65; 9. Якому закону розподілу підпорядко-вуються такі ознаки: верхній артеріальний тиск, довжина судин, розміри органів, вага та об’єм мозку. B) нормальному закону розподілу (Гауса); 10. Математичне сподівання дискретної випадкової величини розраховується за формулою: B) 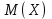 = = 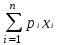 ; ;11. Незалежна випадкова величина X задана рядом розподілу:
Математичне сподівання рівне: A) 4,2; 12. Випадкова величина Х задана функцією щільності розподілу: 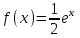 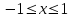 . .Якою формулою виражатиметься функція розподілу випадкової величини? C) 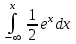 ; ;13. З партії таблеток обсягом n=40 знайдено середню массу m = 0,5г таблетки та оцінки дисперсії 2,5∙10-5 г2. Значення середньо-квадратичного відхилення рівне: E) 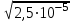 . . 14. При визначення рівня тиску в крові (мм. водн.ст.) в капілярах отримані дані: 16, 16, 15, 20, 20, 18, 35, 17, 19, 38. Чому дорівнює точкова оцінка середнього значення даних вимірювань? A) 19,6; 15. Математичне сподівання випадкових величин M(X)=4, а M(Y)= 1. Математичне сподівання M(X - Y) рівне: C) 3; 1. Ряд розподілу випадкової величини це: B) таблиця, в якій кожному значенню випадкової величини ставиться у відповідність її ймовірність; 2. Неперервна випадкова величина задається функцією: 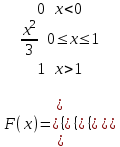 . . Функція щільності розподілу на проміжку 0 ≤ x ≤ 1 дорівнює: D) 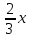 ; ;3. Емпірична функція розподілу F(x) для дискретної випадкової величини визнача-ється як: A) нагромадження відносної частоти 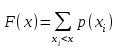 ; ;4. Для контролю якості розчинів в ампулах для ін’єкцій із серії 8000 ампул вибрали 630. Яка із сукупностей є генеральною? A) n = 8000; 5. Математичне сподівання для неперевної випадкової величини розраховують за формулою: B) 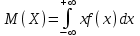 ; ;6. При дослідженні сироватки крові на холестерин (мг %) у n=9 чоловіків (46-50 років) під час гіпертонічного кризу вибіркове середнє значення 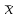 =23%. Чи є дане вибіркове середнє оцінкою математичного сподівання? =23%. Чи є дане вибіркове середнє оцінкою математичного сподівання?B) так; 7. Яка випадкова величина є неперервною? A) яка приймає будь-яке значення з інтервалу в якому вона існує; 8. Якому закону можуть підпорядковуватися неперервні випадкові величини? C) нормальному закону; 9. Що таке точкове оцінювання хара-ктеристик розподілу досліджуваної ознаки? A) визначення оптимальної оцінки статистичної характеристики; 10. Дисперсія неперервної випадкової величини дорівнює 3,5. Чому дорівнює середньоквадратичне відхилення: A) 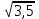 11. Заданий ряд розподілу незалежної випадкової величини Y:
Математичне сподівання рівне: A) 1, 9; 12. Дисперсія від константи 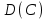 рівна: рівна:C) 0; 13. Вакцина формує імунітет від деякого захворювання з ймовірністю 0,999. Провакциновано 4000 мешканців міста. Якому середньому значенню відповідає число непровакцинованих? D) 4; 14. Випадкова величина X задається функцією щільності розподілу: 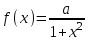 . . 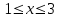 Якою формулою виражатиметься функція розподілу? D) 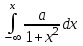 ; ;15. Дисперсія неперервної випадкової вели-чини X дорівнює 9. Чому дорівнює середньо-квадратичне відхилення величини X? D) 3; Поняття про диференціальні рівняння 1. Чи є рівняння 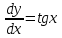 диференціальним? диференціальним?C) так, першого порядку; 2. Загальним розв’язком диференціального рівняння 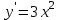 є функція: є функція:B) Y = x3 + C; 3. Для знаходження частинного розв’язку диференціального рівняння з відокремленими змінними необхідно мати початкову умову: C) y (x0) = y0; 4. Диференціальне рівняння записується: 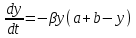 , де β – коефіцієнт пропорційності, а, b – сталі. Якого порядку диферен-ціальне рівняння , де β – коефіцієнт пропорційності, а, b – сталі. Якого порядку диферен-ціальне рівнянняA) першого; 5. Яке рівняння називають диференціальним? C) яке містить похідну; D) яке містить диференціали у і х; 6. Як знайти частинний розв’язок диференціального рівняння першого порядку? E) знайти загальний розв’язок, підставити початкові умови в загальний розв’язок, знайти константу С і підставити у загальний розв’язок. 7. Чи є рівняння 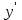 = xy4 диференціальним рівнянням? = xy4 диференціальним рівнянням?А) так; 8. Швидкість скорочення м’язу описується диференціальним рівнянням 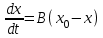 , де В – стала, х0 – повне скорочення м’язу, х – скорочення в момент t. Що виражає загальний розв’язок рівняння? , де В – стала, х0 – повне скорочення м’язу, х – скорочення в момент t. Що виражає загальний розв’язок рівняння?B) закон скорочення м’язу в момент часу t; 9. Загальним розв’язком диференціального рівняння 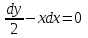 є функція: є функція:B) 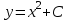 ; ;10. 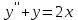 . Якого порядку задане диференціальне рівняння? . Якого порядку задане диференціальне рівняння?D) другого; 11. Що виражає формула 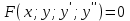 ? ?В) загальний вигляд диференціального рівняння другого порядку; 12. Ріст клітини визначається потоком поживних речовин через її оболонку. На ранніх стадіях, що маса клітини пропорційна до площі поверхні. Нехай клітина має форму кулі. Тоді процес опишеться рівнянням: 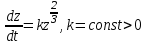 . Що виражає загальний розв’язок? . Що виражає загальний розв’язок?В) залежність маси клітини 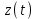 від часу від часу 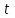 ; ;13. Зміна розміру популяції бактерій 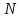 з часом з часом 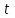 в годинах описується диференціальним рівнянням в годинах описується диференціальним рівнянням 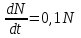 . Яким буде загальний розв’язок? . Яким буде загальний розв’язок?С) 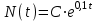 ; ;14. Диференціальне рівняння розвитку епідемії має вигляд 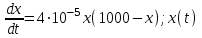 - число носіїв інфекції в момент часу - число носіїв інфекції в момент часу 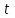 . Що означає загальний розв'язок диференціального рівняння? . Що означає загальний розв'язок диференціального рівняння?А) закон зростання числа носіїв інфекції; 15. Перевірити, яка функція є розв’язком диференціального рівняння: 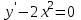 : :Е) 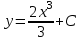 . .1. Задане рівняння 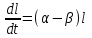 , де l – довжина клітини, α і β – сталі є: , де l – довжина клітини, α і β – сталі є:D) диференціальним рівнянням першого порядку; 2. Розв’язок диференціального рівняння 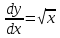 буде: буде:C) у = 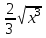 + С; + С;. 3. Задане рівняння виду 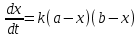 , де , де 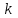 – коефіцієнт пропорційності, а, b – сталі. Чи є рівняння диференціальним? – коефіцієнт пропорційності, а, b – сталі. Чи є рівняння диференціальним? B) диференціальним рівнянням першого порядку; 4. Інтегральна функція концентрації препарату для однокамерної лінійної моделі із всмоктуванням має вигляд 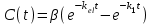 . Що виражає інтегральна функція концентрації препарату? . Що виражає інтегральна функція концентрації препарату?A) рівень концентрації препарату; 5. Як визначається порядок диференціального рівняння? A) порядком похідної у рівняння; B) порядком диференціалу у рівняння; 6. Яка функція є загальним розв’яком диференціального рівняння 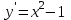 ? ?E) 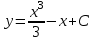 . .7. Рівняння виду 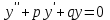 , p, q – константи є: , p, q – константи є:D) лінійним диференціальним рівнянням другого порядку зі сталими коефіцієнтами; . 8. Загальним розв’язком диференціального рівняння 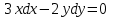 є функція: є функція:E) 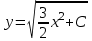 . .9. Популяція бактерій росте так, що швидкість її росту в момент часу t дорівнює розміру популяції N, поділеній на 10. Як опишеться цей процес? C) 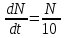 ; ;10. Чи є рівняння 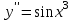 диференціальним рівнянням? диференціальним рівнянням?B) другого порядку; 11. Яка функція є загальним розв’язком диференціального рівняння 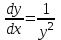 ? ?Е) 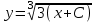 . .12. Множину розв’язків диференціального рівняння 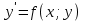 представимо формулою: представимо формулою: 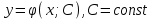 . Що виражає дана формула? . Що виражає дана формула?А) загальний розв’язок диференціального рівняння; 13.Дріжджі в розчині ростуть так, що їх маса збільшується зі швидкістю, яка дорівнює половині маси (час вимірюється в годинах). Описати цей процес. В) 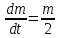 ; ;14. Загальним розв’язком диференціального рівняння 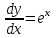 є: є:С) 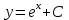 ; ;15. Швидкість зміни порогової сили струму представлена формулою 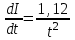 . Що виражає загальний розв'язок рівняння. . Що виражає загальний розв'язок рівняння.А) закон зміни сили струму в момент часу; 1. Загальний розв’язок диференціального рівняння 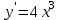 рівний: рівний:C) 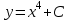 ; ;2. Концентрація деякого лікарського препарату описується диференціальним рівнянням 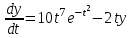 . Якого порядку є дане диференціальне рівняння? . Якого порядку є дане диференціальне рівняння?D) першого порядку; 3. Швидкість зміни маси лікарського препарату однокамерної лінійної фармакокінетичної моделі можна описати диференціальним рівнянням 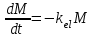 , де kel – константа елімінації. Загальний розв’язок цього рівняння запишеться: , де kel – константа елімінації. Загальний розв’язок цього рівняння запишеться:C) 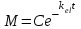 ; ;4. Загальний розв'язок диференціального рівняння 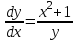 є: є:D) 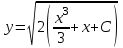 ; ;5. Яке рівняння називається диференціальним першого порядку? A) якщо містить похідну першого порядку; 6. Маса дріжджів в цукрі m (кг) з часом t (год.) змінюється за законом 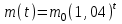 . Чи є дане рівняння диференціальним? . Чи є дане рівняння диференціальним?C) не є диференціальним; 7. Чи є рівняння 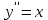 диференціальним рівнянням другого порядку? диференціальним рівнянням другого порядку?A) так; 8. Загальний розв’язок диференціального рівняння 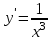 рівний: рівний:D) 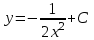 ; ;9. Загальний розв’язок диференціального рівняння 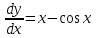 є: є:A) y = 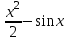 + C; + C;10. Швидкість розпаду пропорційна числу ядер атомів радіоактивної речовини, які не розпалися і записується рівнянням: 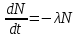 , де N – число ядер атомів, що не розпалися, - постійна розпаду, t – час. Що визначає частинний розв’язок диференціального рівняння при t = 0, N = N0 ? , де N – число ядер атомів, що не розпалися, - постійна розпаду, t – час. Що визначає частинний розв’язок диференціального рівняння при t = 0, N = N0 ?D) кількість ядер атомів, що не розпалися в початковий момент часу; 11. Перевірити, яка з функцій є розв’язком диференціального рівняння 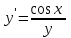 . .А) 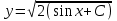 ; ;12. Рівноважний розмір популяції певного виду в окресленому ореалі становить 1000 осіб. Чисельність популяції зазнає флуктуації в околі цього рівноважного розміру і описується диференціальним рівнянням 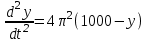 . Якого порядку дане рівняння? . Якого порядку дане рівняння?С) другого; 13. Перевірити, яка з функцій є розв’язком диференціального рівняння 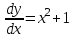 . .Е) 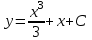 . . |
