База_з_мед_фізики_Мат_стат_;_Диф. Елементи математичної статистики Випадкові величини х поділяються на
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
2. Інтеграл функції 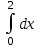 рівний: рівний:B) 2; 3. Інтеграл 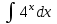 рівний: рівний:D) 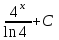 ; ;4. Шлях пройдений тілом при рівномірному русі за проміжок часу [Т0;Т] з швидкістю 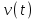 визначається: визначається:A) 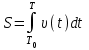 , де υ - швидкість; , де υ - швидкість;5. Невизначений інтеграл 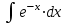 знаходиться методом: знаходиться методом:A) методом підстановки; 6. За допомогою визначеного інтеграла можна обчислити: A) площу фігури обмежену лініями; 7. Швидкість розпаду радіоактивної речовини з таблетки 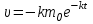 , де k - постійна розпаду, m - маса радіоактивної речовини при t= t0. Як знайти залежність розпаду кількості речовини від часу t? , де k - постійна розпаду, m - маса радіоактивної речовини при t= t0. Як знайти залежність розпаду кількості речовини від часу t?A) треба проінтегрувати швидкість (невизначений інтеграл); 8. Знайти невизначений інтеграл 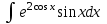 методом: методом:B) методом заміни змінної; 9. Визначений інтеграл обчислюється за формулою Ньютон-Лейбніца: D) 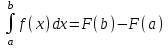 ; ;10. Функція F(x) називається первісною для функції f(x) якщо: B) 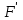 (x) = f(x); (x) = f(x);11. Невизначений інтеграл від алгебраїчної суми двох функцій дорівнює: А) 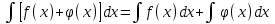 ; ;. 12. Невизначений інтеграл 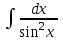 рівний: рівний:А) 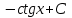 ; ;13. Швидкість утворення продукту хімічної реакції другого порядку описується формулою 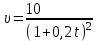 (кг/год). За якою формулою знаходимо кількість продукту реакції, що утворюється за період (кг/год). За якою формулою знаходимо кількість продукту реакції, що утворюється за період 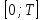 ? ?С) 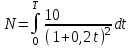 ; ;14. За якою формулою обчислюється площа фігури, обмежена лініями 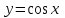 і віссю і віссю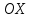 в межах від 0 до в межах від 0 до 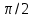 . .В) 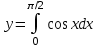 ; ;15. Визначений інтеграл 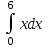 дорівнює: дорівнює:В) 18 ; 1. Невизначений інтеграл це: C) сукупність первісних заданої функції; 2. Інтеграл 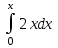 рівний: рівний:C) х2; 3. Формула Ньютона-Лейбніца має вигляд: B) 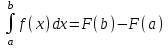 ; ;4. Інтеграл 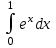 рівний: рівний:E) ≈ 1,7. 5. Інтеграл 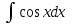 рівний: рівний:C) sin x + C; 6. При вільному падінні швидкість тіла змінюється за законом 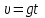 . Яким є рівняння руху тіла? . Яким є рівняння руху тіла?B) 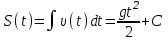 ; ;7. Чому дорівнює вираз 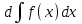 : :E) f(x)dx. 8. Швидкість зміни концентрації препарату з ізотопним індикатором 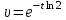 . Як визначити зміну концентрації препарату за період [t1; t2]? . Як визначити зміну концентрації препарату за період [t1; t2]?A) проінтегрувати швидкість υ визначення інтегралом з межами інтегрування [t1; t2]; 9. Визначений інтеграл застосовують для: A) обчислення площі фігур обмежену лініями; 10. Яким методом знайти інтеграл 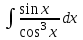 : :B) методом заміни змінної; 11. Невизначений інтеграл від виразу 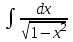 рівний: рівний:А) 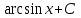 ; ;12. При перестановці місцями меж інтегрування визначений інтеграл: В) змінює знак на „-“; 13. При хімічній реакції вихід речовини відбувається зі швидкістю 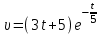 (кг/год), (кг/год), 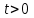 вимірюється в годинах. За якою формулою визначається кількість речовини, що утворюється за період вимірюється в годинах. За якою формулою визначається кількість речовини, що утворюється за період Е) 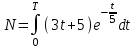 . .14. Фігура обмежена лініями: 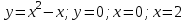 ; за якою формулою обчислити площу? ; за якою формулою обчислити площу?D)  ; ;15. Визначений інтеграл 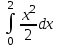 рівний: рівний:А) 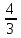 ; ;1. Інтеграл функції 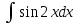 рівний: рівний:D) – 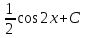 ; ;2. Інтеграл 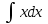 рівний: рівний:E) 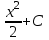 . .3. Інтеграл функції 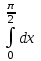 рівний: рівний:C) 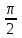 ; ;4. Визначений інтеграл фізично визначає: A) роботу змінної сили; 5. Швидкість росту числа бактерій υ = 2103 t. Як знайти залежність числа бактерій від часу? B) знайти невизначений інтеграл від υ; 6. Чому рівний інтеграл 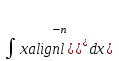 ? (n ≠ –1) ? (n ≠ –1)A) 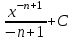 ; ;7. Інтеграл 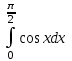 рівний: рівний:D) 1; 8. Якщо існують інтеграли 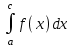 і і 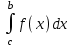 , то: , то:E) 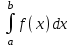 = = 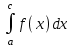 + + 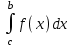 . .9. Обчислення площі фігури, обмеженої лініями 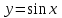 і віссю ОХ при 0 ≤ х ≤ π розраховується за формулою: і віссю ОХ при 0 ≤ х ≤ π розраховується за формулою:C) 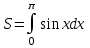 ; ;10. 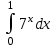 дорівнює: дорівнює:E) 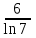 . .11. Невизначений інтеграл від диференціала функції 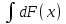 дорівнює: дорівнює:А) 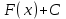 ; ;12. У момент часу 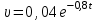 (моль/год). Час (моль/год). Час 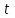 вимірю-ється в годинах. За якою формулою визначається зміна кількості препарату в крові за період вимірю-ється в годинах. За якою формулою визначається зміна кількості препарату в крові за період 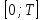 ? ?С) 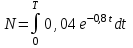 ; ;13. . Фігура обмежена лініями: 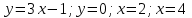 ; за якою формулою обчислити площу? ; за якою формулою обчислити площу?D) 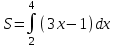 ; ;14. При оберненому розширенні одним молем ідеального газу тиск 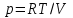 . За якою формулою обчислити виконану роботу при ізотермічному розширенні від . За якою формулою обчислити виконану роботу при ізотермічному розширенні від 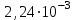 до до 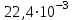 м3 при м3 при 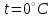 . .В) 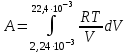 ; ;15. Інтеграл 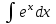 дорівнює: дорівнює:А) 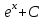 ; ;Елементи теорії ймовірності 1. З 20 людей, які захворіли на грип 12 одужує за три дні. Яка ймовірність того, що випадково вибраний пацієнт не одужає за три дні? C) 2/5; 2. Колонію мікроорганізмів обробляють препаратом B, що дає 60% знищення мікроорганізмів. Надійність даного препарату рівна: D) 0,6; 3. В контрольно-аналітичній лабораторії є один вимірювальний прилад. Ймовірність того, що він працює 0,8. Ймовірність того, що в даний момент часу прилад не працює рівна: D) 0,2; 4. Які події є випадковими? C) події, які відбуваються і можуть не відбуватися за даних умов; 5. З 100 випробувань подія А випадає 10 раз. Ймовірність випадання події А рівна: C) 0,1; 6. Подія А має протилежну 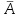 . Ймовірність протилежної події розраховується за формулою: . Ймовірність протилежної події розраховується за формулою:C) 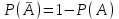 ; ;7. Події А і В залежні. Ймовірність події В при умові, що А відбулася визначають за формулою: C) 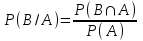 ; ;8. На обстеження прибула група з 10 осіб. Троє із них хворі. Лікар запрошує до кабінету по 2 особи. Знайти ймовірність того, що перших двоє є хворі: D) 1/15; 9. Чому дорівнює відносна частота випадкових подій, де n – кількість випро-бувань, m – реалізації події А з n: B) m/n; 10. Стрілок влучає у ціль при кожному пострілі з ймовірністю 0,8. Визначити ймовірність того, що зробивши два постріли він два рази влучить у ціль. B) 0,64; 11. В полі спостереження мікроскопа біоло-гічна клітина. За час спостереження клітина може поділитися і може не поділитися. Чому дорівнює ймовірність того, що клітина не поділиться? A) 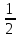 ; ;12. При аварії постраждали 12 людей; 4 з них дістали опіки. Швидка допомога завозить в лікарню по 2 потерпілі. Знайти ймовірність того, що в машині опиняться обидва потерпілих з опіками. C) 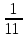 ; ;13. Під час епідемії 12% населення міста захворіло. Кожен четвертий хворий викликає лікаря. Яка ймовірність того, що довільний мешканець цього міста викликатиме лікаря. A) 0,03; 14. Відомо, що 5% чоловіків певної області – дальтоніки. Навмання обирається особа, яка виявилася дальтоніком. Якій ймовірності відповідає дане процентне значення? B) 0,05; 15. У спеціалізовану лікарню поступає в середньому 50% пацієнтів із захворюванням А, 30% – із захворюванням В, 20% – із захворюванням С. Знайти ймовірність того, що пацієнт, який поступив у лікарню не має захворювання С. E) серед відповідей немає правильної. 1. З 400 обстежених чоловіків, що палять, 200 мають захворювання легень. Ймовірність захворювання легень чоловіків, що палять рівна: A) 0,5; 2. Згідно статистики зі 700 новонароджених один хлопчик народжується з зайвою Y-хромосомою. Яка ймовірність того, що новонароджений хлопчик без зайвої хромосоми? C) 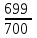 ; ;3. При обстеженні 300 студентів флюоро-графією виявлено наступні захворювання: 5 студентів – плеврит, 8 – залишкові явища після пневмонії. Статистична ймовірність захворювань, виявлених за допомогою флюорографії серед студентів рівна: A) 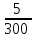 ; ;B) 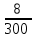 ; ;4. В сім’ї чекають дитину. Ймовірність народження хлопчика 0,55. Ймовірність народження дівчинки рівна: D) 0,45; 5. Два фармацевтичних підприємства виготовляють один і той же препарат. Ймовірність виготовлення препарату на першому підприємстві 0,4, на другому – 0,6. Навмання взято дві упаковки. Яка ймовірність того, що вони з різних підприємств. D) 0,24; 6. Монету підкидають 10 разів. Цифра випадає чотири рази. Статична ймовірність випадання цифри дорівнює: D) 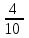 ; ;7. Які події називають незалежними? C) якщо можливість реалізації однієї події не залежить від того, чи відбулася друга у цих можливих випробуваннях; 8. Які значення може приймати ймовірність випадкової події Р(А): D) 0 ≤ Р(А) ≤ 1; 9. Хворому необхідно зробити переливання крові. Ймовірність того, що група крові виявиться придатною дорівнює 0,3. Яка ймовірність того, що у випадково вибраного донора група крові непридатна до переливання? B) 0,7; 10. В ящику знаходиться 5 білих, 3 чорні і 2 червоні кулі. Не дивлячись, з ящика виймають дві кулі. Яка ймовірність того, що обидві кулі чорні, якщо перша вийнята куля повертається назад в ящик до того як буде вийнята друга куля? B) 0,09; 11. Серед усіх родин з двома дітьми обрано одну. Яка ймовірність того, що в цій родині є одна дівчинка? B) 0,5; 12. На певному ареалі є 100 співіснуючих видів тварин. Визначимо 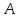 – як множину видів, які живляться вдень, що становить 60%, а – як множину видів, які живляться вдень, що становить 60%, а 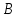 – як множину видів, які живляться вночі, що становить 40%. Яким ймовірностям відповідають ці процентні значення? – як множину видів, які живляться вночі, що становить 40%. Яким ймовірностям відповідають ці процентні значення?C) 0,6; 0,4; 13. В лотереї n= 30 квитків, з яких 4 виграшних. Яка ймовірність виграшу власника одного лотерейного квитка? D) 4/30; 14. При обробці поля певним отрутохімікатом гине 80% жуків. Яка ймовірність того, що при обробці поля даним препаратом жуки не загинуть? B) 0,2; 15. В одній великій спеціалізованій лікарні згідно оцінкам 40% чоловіків мають серйозне порушення серцевої діяльності. Якій ймовірності відповідає дане процентне значення? C) 0,4; 1. Які події називаються залежними? A) події, реалізація яких обумовлена; . 2. Події А і В незалежні і несумісні. Ймовірність появи однієї з цих двох подій визначається формулою: A) 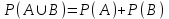 ; ;3. Задані ймовірності 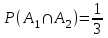 , , 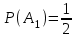 . Ймовірність . Ймовірність 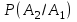 дорівнює: дорівнює:A) 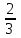 ; ;4. На обстеження прибула група з 20 осіб. Четверо із них хворі. Лікар запрошує до кабінету по одній особі. Знайти ймовірність того, що пацієнт здоровий. D) 4/5; 5. Згідно зі статистичними даними 36,9% населення Європи мають групу крові А. Яка ймовірність того, що випадковий зустрічний має групу крові А? B) 0,369; 6. При захворюванні шлунку ймовірність встановлення правильного діагнозу за допомогою ендоскопії 80%. Якій ймовірності відповідає дане процентне значення? A) 0,8; 7. На фармацевтичному заводі відділом технічного контролю серед 100 перевірених одиниць лікарського препарату 10 не відповідало стандарту. Ймовірність відхи-лення від стандарту рівна: C) 0,1; 8. Які події утворюють повну групу подій? A) не сумісні; 9. У вузі три факультети. Кількості студентів які навчаються на них співвідносяться як 11:15:19. Доля спортсменів-розрядників становить на цих факультатех відповідно 10, 20 і 5 %. Яким ймовірностям відповідає дане процентне співідношення спортсменів-розрядників? B) 0,1: 0,2: 0,05; 10. Серед партії 500 ампул перевірених на герметичність 10 ампул виявились із дефектами. Чому дорівнює статистична ймовірність ампули з дефектом? D) 0,02; 11. 33 букви українського алфавіту написані на картках розрізної азбуки. Яка ймовірність того, що навмання вибрана картка є буква «А»? C) 1/33; 12. В клітці тримають 8 білих і 4 сірих мишей. Яка ймовірність того, що навмання вибрана миша буде біла? B) 2/3; 13. Задані ймовірності 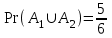 ; ; 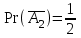 .Знайти ймовірності .Знайти ймовірності 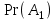 ; ;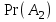 B) 1/3;1/2; 14. Три оператори радіолокаційного приладу проводять спостереження, допускаючи 5%, 4% і 2% помилки. Яким ймовірностям відповідають ці процентні значення? E) 0,05; 0,04; 0,02. 15. Краснуха може бути причиною серйозних вроджених вад розвитку у дітей, якщо мати хворіє нею на ранніх стадіях вагітності. Ймовірність вад оцінюється як 45%. Яка ймовірність того, що новонароджена дитина не матиме вади? B) 0,55; 1. Під час лікування нирок за певною методикою одужує 75 % пацієнтів. Лікується 2307 хворих. Яка надійність даної методики? D) 0,75; 2. Аптечний склад отримує медикаменти з міст А і В. Ймовірність отримання медика-ментів з міста А є такою Р(А) = 0,6. Ймовірність отримання медикаментів з міста D) 0,4; |
