База_з_мед_фізики_Мат_стат_;_Диф. Елементи математичної статистики Випадкові величини х поділяються на
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
Елементи математичної статистики 1. Випадкові величини Х поділяються на: E) дискретні і неперервні. 2. Сила стуму вимірюється амперметром класу точності 1,5. Отримані такі результати: 0,3; 0,28; 0,31; 0,31; 0,3; 0,29; 0,28; 0,32; 0,3 А. Істинне значення сили струму становить: C) 0,3; 3. Дискретна випадкова величина має розподіл:
Математичне сподівання М(х) = 2,3; дисперсія D(х) = 10,4. Яке середньо-квадратичне відхилення? 3,2; 4. Якщо випадкова величина задається біномним законом розподілу, то ця величина B) дискретна; C) інтервальна; 5. Функція розподілу є неспадною при 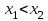 , то має місце нерівність: , то має місце нерівність:C) 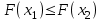 ; ;6. Для яких числових характеристик задається точкова оцінка? B) для математичного сподівання, дисперсії, середньоквадратичного відхилення; . 7. Оцінку дисперсії для дискретної випадкової величини розраховують за формулою: B) 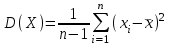 ; ;8. Неперервна випадкова величина задана функцією розподілу: 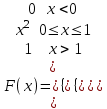 . Чому дорівнює функція щільності розподілу f(x)? . Чому дорівнює функція щільності розподілу f(x)?C) 2х; 9. Якщо випадкова величина задається функцією щільності розподілу: 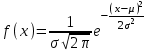 , то це: , то це:B) неперервна випадкова величина; 10. Дисперсія дискретної випадкової величини дорівнює 1,7. Чому рівне середньо-квадратичне відхилення випадкової величини? A) 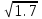 11. Заданий ряд розподілу незалежної випадкової величини Y:
Математичне сподівання рівне: 1,9; 12. Випадкова величина Х задана функцією щільності розподілу: 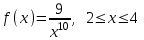 . .Якою формулою виражатиметься функція розподілу? B) 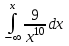 , x є (- , x є (-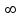 ; ;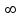 ); );13. Для розрахунку дисперсії неперервної випадкової величини використовують формулу: A) 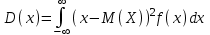 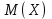 – математичне сподівання; – математичне сподівання; 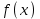 – функція щільності розподілу. – функція щільності розподілу.14. Вимірювання об’єму ампул 1% розчину аскорбінової кислоти в 40% розчині глюкози дало середнє значення 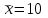 мл з дисперсією мл з дисперсією 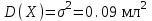 . Чому дорівнює середньоквадратичне відхилення? . Чому дорівнює середньоквадратичне відхилення?B) 0,3; 15. До якого типу випадкових величин можна віднести вагу і зріст людини? C) неперервні; 1. Дано закон розподілу незалежної випадкової величини:
Математичне сподівання випадкової величини дорівнює: C) -0,3; 2. Функція розподілу випадкової величини 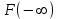 і і 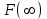 дорівнює: дорівнює:D) 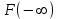 = 0; = 0; 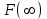 = 1; = 1;3. Для яких випадкових величин має місце функція щільності розподілу? B) неперервних; 4. Яка із заданих формул дозволяє обчислити ймовірність попадання випадкової величини в заданий інтервал 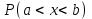 : :E) 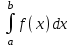 . .5. Для якого варіаційного ряду графічно будують гістограму частот? A) інтервального; B) неперервного;. 6. При визначенні вмісту азоту в даній пробі було отримано результати: 9,28; 9,38; 9,35; 9,43; 9,53; 9,48 %. Якому істинному сере-дньому значенню відповідає вміст азоту в даній пробі? A) 9,41 %; 7. Оцінку середньоквадратичного відхилення розраховують за формулою: A) 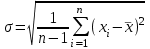 ; ;8. Інтервальною оцінкою для математичного сподівання є проміжок: 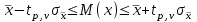 , ,де 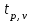 – коефіцієнт Стьюдента, – коефіцієнт Стьюдента, 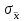 – середньо квадратичне відхилення середнього, – середньо квадратичне відхилення середнього, 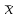 – середнє значення, n – об’єм вибірки. Число ступенів вільності – середнє значення, n – об’єм вибірки. Число ступенів вільності 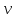 для знаходження коефіцієнта Стьюдента визначається при: для знаходження коефіцієнта Стьюдента визначається при:B) v = n - 1; 9. Функція розподілу безвідмовної роботи медичного приладу має вигляд 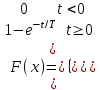 . . Якою є функція щільності розподілу f(t)? E) 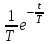 . .10. Дисперсія неперервної випадкової величини рівна 2. Середньоквадратичне відхилення цієї випадкової величини дорівнює: C) 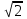 ; ;11. Задані ряди розподілу незалежної випадкової величини X:
Математичне сподівання M(x) рівне: E) 0,1. 12. Випадкова величина задана функцією щільності розподілу: 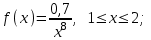 . .Якою формулою виражатиметься функція розподілу? A) 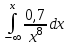 ,x є (- ,x є (-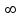 ; ;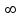 ) )13. Закон розподілу випадкової величини це: A) відповідність між значенням випадкової величини та їх ймовірностей; 14. Функція розподілу випадкової величини виражається формулою: B) 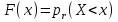 ; ; 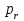 – ймовірність випадкової величини; – ймовірність випадкової величини;15. Згруповані дані про кількість квіток лікарської рослини на одному пагоні утворюють такий ряд розподілу:
Точкова оцінка математичного сподівання дорівнює: A) 3,5; . 1. Ріст людей при статистичному аналізі розглядається як: B) неперервна випадкова величина; 2. Функція розподілу F(x) рівна: D) ймовірності того, що випадкова величина Х приймає значення менше від аргумента; 3. Задано закон розподілу випадкової величини
Дисперсія випадкової величини дорівнює: D) 15,21; 4. Протягом 20 тижнів число невиконаних замовлень фармацевтичною фірмою складає ряд: 12, 15, 18, 16, 12, 15, 18, 16, 14, 12, 14, 12, 16, 13, 13, 14, 16, 15, 4, 8. Як побудувати ряд розподілу? C) поставити значення випадкової величини у порядку зростання з їх ймовірностями; 5. Для контролю якості розчинів в ампулах для ін’єкцій із серії 5000 ампул вибрали 150. Котра із сукупностей є генеральною? A) n = 5000; 6. Математичне сподівання 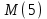 рівне: рівне:B) 5; 7. Ймовірність попадання в інтервал [x1; x2] випадкової величини Х, яка підпорядко-вується нормальному закону розподілу рівна: C) 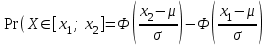 ; ;8. Дискретна випадкова величина має закон розподілу:
Математичне сподівання рівне: B) -0,1; 9. Які параметри визначають розподіл Гауса (нормальний розподіл)? B) математичне сподівання, середньоквадратичне відхилення; 10. Дисперсія незалежної випадкової величини D(X)=16. Середньоквадратичне відхилення дорівнює: A) 4; 11. Незалежна випадкова величина Y задана рядом розподілу:
Математичне сподівання рівне: 7,4; 12. При дослідженні сироватки крові на холестерин (мг %) у чоловіків (46 – 50 рр) під час гіпертонічного кризу отримані наступні результати: 210, 215, 230, 231, 232, 231, 238, 240, 245. Чому дорівнює точкова оцінка середнього значення даних досліджень? B) 230,2; 13. Випадкові величини Х та Y мають математичні сподівання M(X) = 6; M(Y) = 2. Чому рівне M(X+Y)? C) 8; 14. В аптеці 80% лікарських препаратів є у готових формах. В аптеці чотири клієнти. Середнє значення того, що клієнт отримає ліки у готовій формі рівне: B) 3,2; 15. Якщо випадкова велична має нормальний закон розподілу, то … D) величина неперевна; 1. Задано закон розподілу незалежної випадкової величини:
Дисперсія випадкової величини дорівнює: D) 1,44; 2. Інтеграл 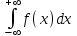 для функції щільності розподілу для функції щільності розподілу 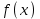 дорівнює: дорівнює:B) 1; 3. Нехай задана неперервна випадкова величина Х і функція розподілу F(x), яка неперервна і диференційована. Тоді функція щільності розподілу f(x) цієї функції визначається: C) 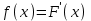 ; ;4. Досліджується ознака Х з математичним сподіванням 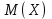 . Нехай n – об’єм вибірки, Δx – ширина класового проміжку; . Нехай n – об’єм вибірки, Δx – ширина класового проміжку; 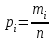 – статистична ймовірність попада-ння в класовий проміжок, тоді значення емпіричної функції щільності розподілу в і-тому проміжку дорівнює – статистична ймовірність попада-ння в класовий проміжок, тоді значення емпіричної функції щільності розподілу в і-тому проміжку дорівнюєA) 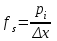 , ,5. Якщо випадкова величина задана законом розподілу Пуассона, то вона: B) дискретна; 6. Якщо k – кількість класів, тоді ширина класового проміжку Δx для інтервального варіаційного ряду рівна: C) 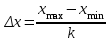 ; ;7. Результати досліджень частоти пульсу людини у стані бадьорості наступні: 76; 73; 68; 83; 71; 62; 55; 63; 46; 59; 54. Середнє значення частоти пульсу рівне: C) 64,6; |
