База_з_мед_фізики_Мат_стат_;_Диф. Елементи математичної статистики Випадкові величини х поділяються на
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
14. При лікуванні на схуднення, одноденні втрати маси були пропорційні масі пацієнта. Яким диференціальним рівнянням описується маса пацієнта, як функція часу? А) 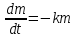 ; ;15. Рівняння виду 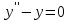 є: є:В) диференціальне рівняння другого порядку; 1. Загальним розв’язком диференціального рівняння 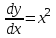 буде: буде:B) 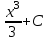 ; ;2. Загальним розв’язком диференціального рівняння 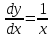 буде: буде:A) у = ln x + C; 3. Рівняння виду 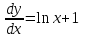 є: є:D) диференціальним рівнянням першого порядку; 4. Якого порядку є диференціальне рівняння 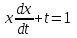 : :A) першого; 5. Загальним розв’язком диференціального рівняння 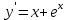 є єE) 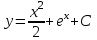 . .6. Швидкість руйнування клітин у постійному звуковому полі записується диференціальним рівнянням 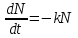 , де N – концентрація клітин, t – час, k – стала. Що виражає розв’язок цього рівняння? , де N – концентрація клітин, t – час, k – стала. Що виражає розв’язок цього рівняння?C) кількість незруйнованих клітин Nв момент часу 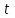 ; ;7. Яке з заданих рівнянь є диференціальним рівнянням другого порядку? D) 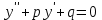 ; ;8. Продукт хімічної реакції першого порядку утворюється зі швидкістю  , де t – час у секундах, m - кількість речовини, що утворюється. Як виразити це диференційним рівнянням? , де t – час у секундах, m - кількість речовини, що утворюється. Як виразити це диференційним рівнянням?A)  ; ;9. Рівняння виду  є. є. C) диференціальним рівнянням другого порядку; 10. Швидкість охолодження тіла записується рівнянням  , де k – коефіцієнт пропорційності, t – час, T, Tc – температура. Який закон виражає загальний розв’язок рівняння? , де k – коефіцієнт пропорційності, t – час, T, Tc – температура. Який закон виражає загальний розв’язок рівняння?B) охолодження тіла в залежності від часу; 11. На дію стимулятора зміни функціональної роботи органу  залежно від часу залежно від часу  (в годинах) моделюється диференціальним рівнянням (в годинах) моделюється диференціальним рівнянням  , ,  - сталі. Який порядок диференціаль-ного рівняння? - сталі. Який порядок диференціаль-ного рівняння?А) перший; 12. Тиск насиченої пари (в області невисокого тиску) при зміні температури на величину 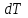 змінюється за законом: змінюється за законом: 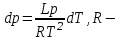 універсальна газова стала; універсальна газова стала;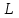 –мольна теплота випаровування. Який зміст загального розв’язку даного диференціаль-ного рівняння. –мольна теплота випаровування. Який зміст загального розв’язку даного диференціаль-ного рівняння.С) залежність тиску насиченої пари від температури; 13. Рівняння виду 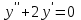 є: є:Е) диференціальне рівняння другого порядку. 14. Загальним розв’язком диференціального рівняння 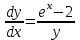 є: є:D) 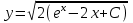 ; ;15. Рівняння виду 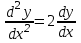 є: є:В) диференціальне рівняння другого порядку; 1. Закон розмноження бактерій з плином часу записується рівняння: 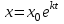 . Чи є задане рівняння диференціальним? . Чи є задане рівняння диференціальним?C) не є диференціальним рівнянням; 2. Розв’язком диференціального рівняння 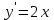 є функція: є функція:B) Y = x2 + C; 3. Яке співвідношення є загальним розв’язком диференціального рівняння 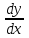 = x = xD) y = 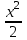 + C; + C;4. Диференціальне рівняння розвитку епідемії записується 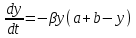 , де β – коефіцієнт пропорційності, а – число носіїв інфекції, b – число здорових осіб сприйнятливих до інфекції. Розв’язок якого є: , де β – коефіцієнт пропорційності, а – число носіїв інфекції, b – число здорових осіб сприйнятливих до інфекції. Розв’язок якого є: 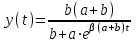 . Що означає розв’язок даного рівняння? . Що означає розв’язок даного рівняння?B) закономірність зменшення здорових осіб з часом; 5. Розв’язком диференціального рівняння 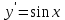 є функція: є функція:A) 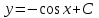 ; ;6. Чи є рівняння 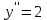 диференціальним рівнянням другого порядку? диференціальним рівнянням другого порядку?B) так; 7. Швидкість розчинення лікарських форм речовини з таблеток описується диференціальним рівнянням першого порядку  , де k – постійна швидкості розчинення, t – час, m – кількість речовини, що нерозчинилася. Який зміст дає загальний розв’язок диференціального рівняння? , де k – постійна швидкості розчинення, t – час, m – кількість речовини, що нерозчинилася. Який зміст дає загальний розв’язок диференціального рівняння?D) маса нерозчиненої лікарської форми речовини з таблетки; 8. Концентрація деякого лікарського препарату в крові після прийому перорально є функцією часу y(t), яка задовольняє диференціальне рівняння:  . Який зміст розв’язку диференціаль-ного рівняння? . Який зміст розв’язку диференціаль-ного рівняння?B) відображає залежність концентрації цієї лікарської речовини в крові від часу; 9. Загальний розв’язок диференціального рівняння  виражається функцією: виражається функцією:E)  . .10. Чи рівняння виду  є диференціальним? є диференціальним?A) ні; . 11. Трансмембранна різниця потенціалів  при поширенні вздовж нервового волокна описується диференціальним рівнянням: при поширенні вздовж нервового волокна описується диференціальним рівнянням:  , ,  – шлях поширення імпульсу; – шлях поширення імпульсу; 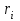 –внутрішній опір; –внутрішній опір; 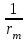 –провідність мембрани. Який порядок рівняння? –провідність мембрани. Який порядок рівняння?С) другий; 12. Яка функція є загальним розв’язком рівняння 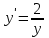 : :С) 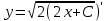 ; ;13. Рівняння виду 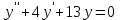 є: є:В) диференціальне рівняння другого порядку; 14. Швидкість розпаду радію пропорційна його кількості. Яким рівнянням виражається цей процес? В) 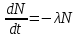 ; ;15. Рівняння 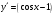 має розв’язок: має розв’язок:Е) 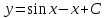 . .Основи диференціального числення 1. Похідною функції називають: границю відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля ; 2. Похідна функції 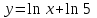 рівна: рівна:Е) 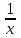 . .3. Похідна функції y = sin3x рівна: В) 3 cos 3x; 4. Мінімум функція 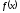 має, коли має, коли 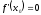 і при переході через точку змінює знак з: і при переході через точку змінює знак з:B) – на +; 5. Диференціювання функції 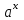 визначається формулою: визначається формулою:В) 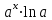 ; ;6. Функція є монотонно спадною, якщо: А) перша похідна < 0; . 7. Похідна від складеної функції 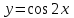 дорівнює: дорівнює:С) 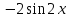 ; ;8. Найбільше значення функції 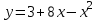 на відрізку на відрізку 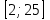 дорівнює: дорівнює:В) 19; 9. Частинна похідна функції двох змінних z = x2 + 2y2 по змінній у рівна: C) 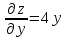 ; ;10. Диференціал y = 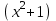 рівний: рівний:B) 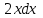 ; ;11. Частинна похідна 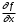 для функції: f(x, y) = x3y2 рівна: для функції: f(x, y) = x3y2 рівна:D) 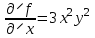 ; ;12. Точка рухається прямолінійно по закону S(t) = 4et (м). Прискорення прямолінійного руху це: B) друга похідна від даного рівняння; 13. Диференціал функції експонентного розподілу F(x) = 1 – e-x дорівнює: C) +e-xdx; 14. Зміщення у відповідь на м’язове подразнення (одиничний імпульс) описується рівнянням y=kte-t/2. Як визначити швидкість процесу: A) знайти першу похідну від виразу; 15. Кількість речовини 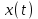 , яка утворюється при хімічних реакціях другого порядку за час , яка утворюється при хімічних реакціях другого порядку за час 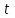 , визначається за формулою: , визначається за формулою: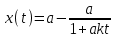 . Якою формулою виразити швидкість реакції? . Якою формулою виразити швидкість реакції?D) v 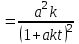 ; ;1. Похідна функції у = е–х рівна: B) –e-x; 2. Похідна функції у = lnх2 рівна: B) 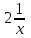 ; ;3. Коливання камертона проходить за законом х = 0,2Аsin800πt. Швидкість коливання камертона знаходиться як: C) перша похідна від заданого рівняння по t; 4. У середовище вносять 1000 бактерій. Чисельність у бактерій зростає за такою залежністю: 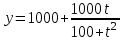 , де t – час. Максимальна кількість бактерій буде коли: , де t – час. Максимальна кількість бактерій буде коли:A) у = 0 і визначивши t підставляємо у початкове рівняння отримаємо у; 5. Формула для диференціювання функції 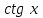 виражається: виражається:D) 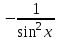 ; ; 6. Функція монотонно зростає, якщо: А) перша похідна > 0; 7. Похідна від складеної функції 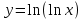 дорівнює: дорівнює:С) 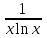 ; ;8. Найменше значення функції 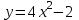 на відрізку на відрізку 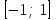 дорівнює: дорівнює:В) 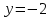 ; ;9. Диференціал від частки двох функцій 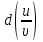 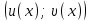 виражається формулою: виражається формулою:C) 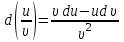 ; ;10. Частинна похідна 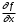 для функції f(x, y) = x2 + y2 рівна: для функції f(x, y) = x2 + y2 рівна:C) 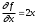 ; ;11. Диференціал функції у = f(x) виражається формулою: 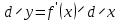 ; ;12. Повний диференціал від функції z(x, y) = х2+2у3 дорівнює: D) dz = 2xdx+6y2dy; 13. Залежність між кількістю х речовини, отриманої врезультаті хімічної реакції і часом t виражається рівнянням x(t) = c(1 – e-kt); k, c – const. Швидкість реакції дорівнює: D) cke-kt; 14. Диференціал функції у = ln(x2 + 1) рівний: C) 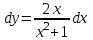 ; ;15. Дріжджі ростуть у цукровому розчині, причому їх маса збільшується на 3 % за кожну годину. Якщо початкова маса становить 1 кг, то маса через 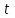 год. буде дорівнювати год. буде дорівнювати 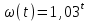 .Як виразиться швидкість зміни .Як виразиться швидкість зміни 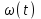 ? ?А) 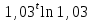 ; ;1. Похідна функції у =е2х – 1 рівна: D) 2е2х – 1; 2. Похідна функції 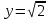 рівна: рівна:A) 0; 3. Перша похідна функції продукту хімічної реакції визначає: A) швидкість хімічної реакції; 4. Хворому роблять ін’єкцію в момент часу t = 0. Концентрація лікарського препарату в крові в момент t описується рівнянням x(t) = c(e-at– e-bt), a, b, c – const, a<b. Для визначення максимального значення концентрації ліків у крові в момент часу t: A) необхідно взяти першу похідну з даного рівняння, прирівняти до нуля і знайти значення t, а потім підставити у вихідне рівняння; |
