База_з_мед_фізики_Мат_стат_;_Диф. Елементи математичної статистики Випадкові величини х поділяються на
 Скачать 0.55 Mb. Скачать 0.55 Mb.
|
|
5. Формула диференціювання складеної функції 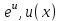 дорівнює: дорівнює:А) 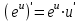 ; ;Е) серед відповідей немає правильної. 6. Диференціал суми двох функцій 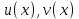 рівний: рівний:С) 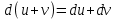 ; ;7. Найбільше значення функції 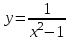 на проміжку на проміжку 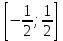 рівне: рівне:D) 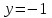 ; ;8. Частинна похідна 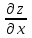 від функції від функції 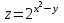 рівна: рівна:А) 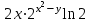 ; ;9. Частинна похідна функції двох змінних z = x2 + 2y2 по змінній у рівна: C) 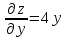 ; ;10. Похідна функції двох змінних z = ln(xy) по змінній х 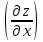 рівна: рівна:B) 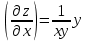 ; ;11. Частинна похідна 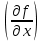 для функції для функції 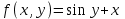 рівна: рівна:C) 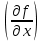 = 1; = 1;12. Диференціал від константи с дорівнює: B) 0; 13. Повний диференціал від функції 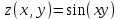 є: є:E) dz = y cos (xy)dx + x cos (xy)dy. 14. Диференціал першого порядку від функції у = 3 cos(x2 + 1) становить: D) dy = –6x sin (x2+1)dx; 15. Розчинення лікарських речовин з таблеток підпорядковується рівнянню 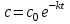 , де , де 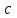 - кількість лікарської речовини в таблетці, яка залишилася до часу розчинення - кількість лікарської речовини в таблетці, яка залишилася до часу розчинення 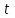 ; ;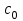 - вихідна кількість лікарської речовини в таблетці; - вихідна кількість лікарської речовини в таблетці; 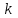 - постійна швидкості розчинення. Чому дорівнює швидкість розчинення лікарських речовин з таблеток? - постійна швидкості розчинення. Чому дорівнює швидкість розчинення лікарських речовин з таблеток?В) v 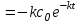 ; ;1. Похідна функції у = х2+3 рівна: D) 2х; 2. Похідна функції 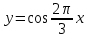 рівна: рівна:A) 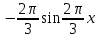 ; ;3. Друга похідна від функції продукту хімічної реакції визначає: B) прискорення хімічної реакції; 4. Максимум функція 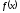 має, коли має, коли 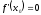 і при переході через точку змінює знак з: і при переході через точку змінює знак з:A) + на –; 5. Диференціал від частки двох функцій 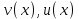 визначається формулою: визначається формулою:А) 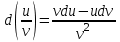 ; ;6. Функція 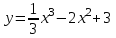 на відрізку на відрізку 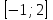 приймає найбільше значення: приймає найбільше значення:А) 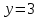 ; ;. 7. Зміщення у відповідь на м’язове подразнення одиничним імпульсом описується рівнянням 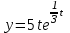 , , 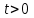 . Як визначити швидкість зміщення залежно від часу? . Як визначити швидкість зміщення залежно від часу?А) знайти першу похідну; 8. Диференціал функції 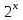 виразиться формулою: виразиться формулою:В) 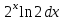 ; ;9. Як знайти максимальну швидкість окиснення азоту, якщо рівняння кінетики має вид v = k(100x2 – x3), де k – стала, х – концентрація окису азоту: D) необхідно з рівняння 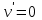 і знайти xі підставити у формулу; і знайти xі підставити у формулу;10. Частинна похідна функції двох змінних z = exy по змінній х рівна: B) 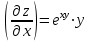 ; ;11. Частинна похідна 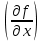 для функції для функції 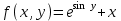 рівна: рівна:D) 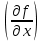 = 1; = 1;12. Диференціал функції 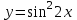 є: є:B) dy = 4sin 2xcos 2xdx; 13. Повний диференціал використовують: C) для визначення граничної похибки посередніх вимірювань; В) 1; 14. Повний диференціал від функції двох змінних z(x, y) виражається формулою: D) 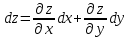 ; ;15. Частинна похідна 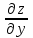 функції функції 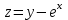 дорівнює: дорівнює:С) У 1. Похідна функції 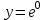 рівна: рівна:C) 0; 2. Перша похідна функції фізично означає: A) швидкість процесу; 3. Похідна функції 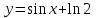 рівна: рівна:A) 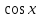 ; ;4. Умовою спадання функції 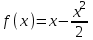 є: є:D) 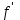 < 0; < 0;5. Похідна функції 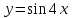 рівна: рівна:D) 4cos 4x; 6. Форму комплексу потенціалів, яка виникає при збуджені сітківки ока світлом виражається рівнянням: 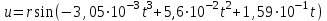 , де r – стала, t – час. Швидкість зміни потенціалів визначається: , де r – стала, t – час. Швидкість зміни потенціалів визначається:першою похідною від даного рівняння; 7. Формула для диференціювання функції 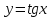 визначається: визначається:С) 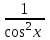 ; ;8. Похідна складеної функції 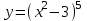 дорівнює: дорівнює:А) 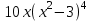 ; ;9. Найменше значення функції 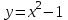 на відрізку на відрізку 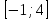 рівне: рівне:С) 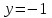 ; ;10. Диференціал добутку двох функцій 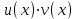 дорівнює: дорівнює:С) 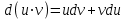 ; ;11. Частинна похідна функції двох змінних 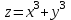 по змінній у рівна: по змінній у рівна:C) 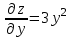 ; ;12. Відомо, що якщо полімерні молекули утворюються шляхом рекомбінації, то мольна доля у молекули полімеру з числом ланцюгів х має вид: 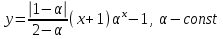 . Для знаходження максимального розподілу по молекулярній масі потрібно спочатку: . Для знаходження максимального розподілу по молекулярній масі потрібно спочатку:B) знайти першу похідну і прирівняти її до нуля; 13. Диференціал функції 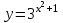 дорівнює: дорівнює:D) 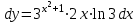 ; ;14. Повний диференціал функції 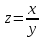 дорівнює: дорівнює:A) 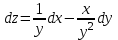 ; ;15. Частинна похідна 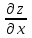 від функції від функції 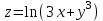 рівне: рівне:А) 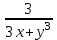 ; ;Основи інтегрального числення 1. Інтеграл функції 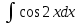 рівний: рівний:A) 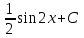 ; ;2. Інтеграл 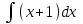 рівний: рівний:E) 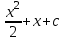 . .3. Інтеграл функції 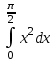 рівний: рівний:C) 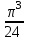 ; ;4. Визначений інтеграл геометрично визначає: D) площу криволінійної трапеції; 5. Методами інтегрування є: C) безпосереднє інтегрування, метод заміни змінної, інтегрування частинами; 6. В умовах необмежених ресурсів харчування швидкість росту популяції 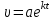 , а – const. Як виразиться чисельність популяції за час від t1 до t2: , а – const. Як виразиться чисельність популяції за час від t1 до t2:B) 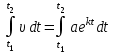 ; ;7. Визначений інтеграл обчислюється за формулою: D) 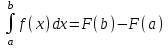 ; ;8. Невизначений інтеграл від виразу 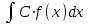 , де С – const рівний: , де С – const рівний:C) 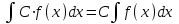 ; ;9. Швидкість руху тіла 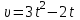 (м/с). Якою формулою виразиться шлях пройдений тілом за 5с від початку руху? (м/с). Якою формулою виразиться шлях пройдений тілом за 5с від початку руху?C) 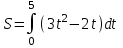 ; ;10. Визначений інтеграл від суми двох функцій 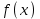 і і 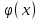 на [a, b] рівний: на [a, b] рівний:D) 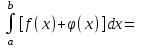 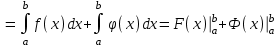 ; ;11. Чому рівний вираз 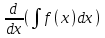 : :А) 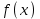 ; ;12. Інтеграл 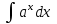 дорівнює: дорівнює:С) 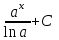 ; ;13. Обчислення площі фігури, обмеженої лініями 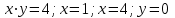 виражається формулою: виражається формулою:А) 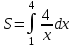 ; ;14. Розвиток епідемії у місті моделюється виразом 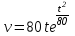 осіб за добу. Час осіб за добу. Час 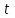 вимірюється днями. Якою формулою запишеться кількість людей, що захворіють за період вимірюється днями. Якою формулою запишеться кількість людей, що захворіють за період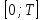 ? ?D) 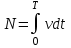 ; ;15. Інтеграл 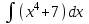 дорівнює: дорівнює:Е) 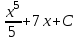 . .1. Приріст чисельності популяції N при заданій швидкості росту 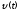 за період Т0 до Т визначається: за період Т0 до Т визначається:D) 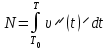 , де – швидкість росту; , де – швидкість росту;2. Інтеграл функції 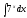 рівний: рівний:D) 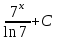 ; ;3. Інтеграл 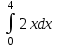 рівний: рівний:D) 16; 4. Інтеграл 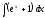 рівний: рівний: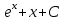 ; ;5. У визначеному інтегралі 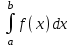 при заміні меж інтегрування з [a, b] на [b, a] отримуємо: при заміні меж інтегрування з [a, b] на [b, a] отримуємо:E) 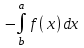 . .6. Швидкість руху тіла виражається формулою 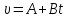 , де А = 5м/с; В = 3м/с2. Шлях пройдений тілом за перші п’ять секунд дорівнює: , де А = 5м/с; В = 3м/с2. Шлях пройдений тілом за перші п’ять секунд дорівнює:D) S = 62,5м; 7. Невизначений інтеграл від f(x) виражається формулою: B) 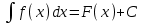 ; ;8. Визначений інтеграл від різниці двох функцій u(x) υ(x) запишеться: B) 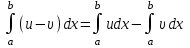 ; ;9. Визначений інтеграл 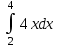 рівний: рівний:B) 24; 10. Інтеграл 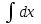 знаходиться методом: знаходиться методом:A) безпосереднього інтегрування; 11. Диференціал від невизначеного інтеграла дорівнює підінтегральному виразу: А) 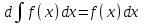 ; ;12. Невизначений інтеграл 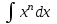 рівний: рівний:С) 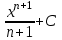 , , 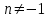 ; ; 13. Інтеграл 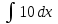 дорівнює: дорівнює:В) 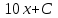 ; ;14. Швидкість приросту популяції описується формулою 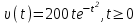 , час вимірюється в роках. За якою формулою знаходимо приріст чисельності популяції за період , час вимірюється в роках. За якою формулою знаходимо приріст чисельності популяції за період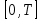 : :D) 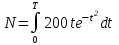 ; ;15. За якою формулою обчислити площу фігури, обмеженою лініями 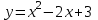 ; ; 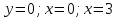 ? ?А) 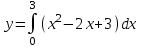 ; ;1. Інтеграл функції 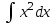 рівний: рівний:A) 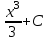 ; ; |
