Вопрос №11. Элементы счисления и их характеристика. Прокладка при отсутствии дрейфа и течения. Счислением координат судна (счислением)

• Название: Элементы счисления и их характеристика. Прокладка при отсутствии дрейфа и течения. Счислением координат судна (счислением)
• Анкор: Вопрос №11.doc
• Дата: 28.05.2018
• Размер: 0.55 Mb.
• Имя файла: Вопрос №11.doc
• Тип: Документы; #19730
• страница: 3 из 4

постоян­ными (элементы течения устойчивые в течение длительного време­ни),

периодическими (элементы течения изменяют направление и скорость в зависимости от приливообразующих сил) и временными (течения, образованные ветром, разностью температур и другими причинами). Сведения об элементах временных течений обычно только ориентировочные.

Рассмотрим плавание на постоянном течении. Под действием упора движителя судно получает движение относительно воды по направлению диаметральной плоскости. Если вода имеет движение относительно Земли, то скорость судна относительно Земли опреде­ляется геометрической суммой



и 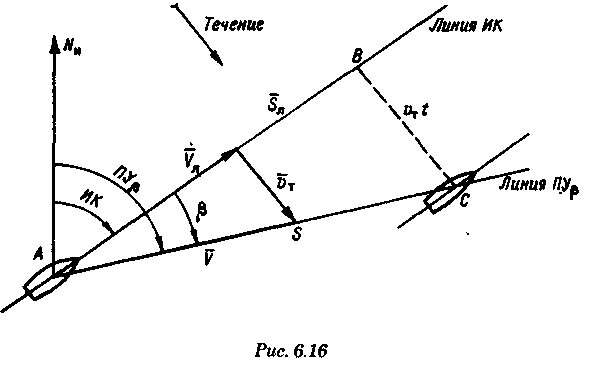судно будет перемещаться по направлению вектора V (рис. 6.16). Если VЛ и vт постоянны по величине и направлению, то V также будет постоянен и судно будет двигаться по прямой АС. Угол ПУβ между северной частью истинного меридиана и направлением движения судна называется путем. Линия АС на­зывается линией пути на течении, а угол β между линией ИК и линией пути называется углом сноса от течения. Скорость V бу­дет являться абсолютной (истинной) скоростью судна (относи­тельно дна).

Из рис. 6.16 видно, что ПУβ = ИК + β.

Знак β зависит от направления сноса. Если течение направлено в левый борт, то β будет иметь знак «плюс», при течении в правый борт — знак «минус». Учет течения сводится к решению треугольни­ка ABC (см. рис. 6.16), который часто называют навигационным. Так же как и при учете дрейфа, различают прямую и обратную задачи. Кроме нахождения угла β, необходимо рассчитать пройденное рас­стояние S. _

П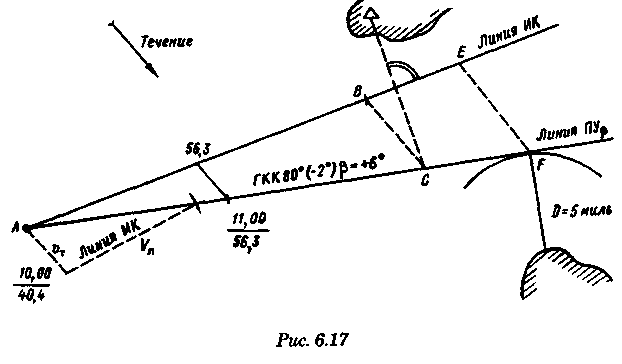рямая задача. В этом случае по заданным ИК, Vл, Кт, и vт требуется рассчитать β, ПУβ и V. Для получения линии пути из точки А прокладываем линию ИК и по ней откладываем скорость судна Vл (скорость, с которой предполагаем следовать данным ИК) в условном масштабе. Обычно берется количество миль в масштабе карты, проходимое за час или полчаса. Из конца вектора V проводим вектор vт в том же масштабе и, соединив точку А с концом вектора vт, получим линию пути судна. Угол β снимается непосредственно с карты. Величину вектора V (истинная скорость) также можно снять с карты. Для получения счислимой точки необходимо отложить исправленную разность отсчета лага по линии ИК и переместить ее по направлению течения на линию пути (точки В и С на рис. 6.17). При длительных переходах, когда курс, и скорость судна, а также элементы тече­ния не меняются, можно вычислять S = Vt (истинное расстояние) и откладывать его по линии пути.

Для расчета отсчета лага или времени прохода судном заданной точки, например точки F (см. рис. 6.17), следует поступить так. Из точки F (судно всегда находится на линии пути) провести линию, па­раллельную течению, до пересечения с линией истинного курса (точ­ка Е). Снять с карты расстояние АЕ, т. е. расстояние, которое судно должно пройти относительно воды. Тогда отсчет лага в точке Е будет равен



Аналогично поступают, когда требуется рассчитать время прихода судна на траверз (или заданный КУ) маяка. Рассчитанный ИП = ИК + КУ проводят до пересечения с линией пути (точка С), затем точку эту по направлению, обратному направлению течения, переносят на линию ИК (точка В). Надписи на карте производятся над линией пути и параллельно ей (см. рис. 6.17). Порядок записи таков: пишется ГКК, в скобках указывается значение принятой по­правки компаса, затем значение угла β с его знаком. Таким образом, направление линии пути равно алгебраической сумме цифр, напи­санной над линией пути судна. У счислимого места на линии пишет­ся время и отсчет лага Значение отсчета лага пишется и на линии истинного курса.

Обратная задача. Необходимо по заданным ПУβ, Vл, Кт, и Vт рассчитать β и ИК.

Задача решается следующим образом. Пусть на карте проложена линия пути судна (см. рис. 6.17). Из начальной точки А прокладыва­ем вектор скорости течения Vт, выраженный количеством миль за полчаса или час. Из конца этого вектора раствором циркуля, равным по абсолютной величине скорости судна Vл за тот же промежуток времени, делаем засечку на линии пути судна. Соединив полученную точку на линии пути с концом вектора течения, получим направле­ние линии ИК судна Полученную линию переносим параллельно в начальную точку А. Если изменятся скорость судна или элементы те­чения, то построение надо делать заново. В этом случае угол β носит название поправки на течение.
Аналитический учет течения

К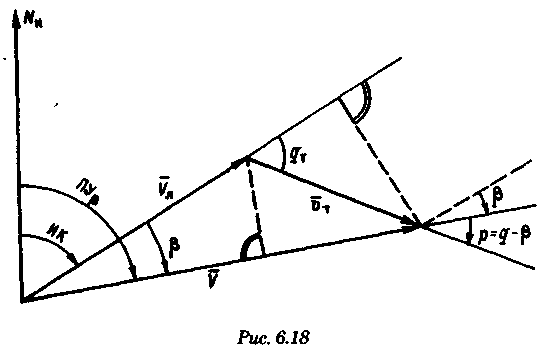роме изложенного графического учета течения существует аналитический учет течения, который принимается при ис­пользовании автоматических счислителей координат. В этом случае угол β выбранный из таблиц вводится как дополнительная поправка курса, а пройденное расстояние получается путем вве­дения дополнительного коэффициента k, т. е. S = Sлk = РОЛ Клk. Получим формулы для β и k прямой задачи (рис. 6.18).

Прямая задача Даны ИК, Vл, Кт, и vт, требуется найти β, ПУβ и V. Построим треугольник скоростей и спроектируем его на линию ИК: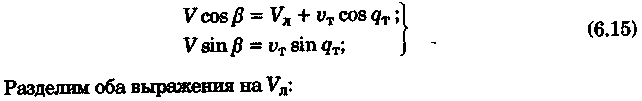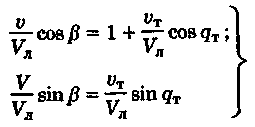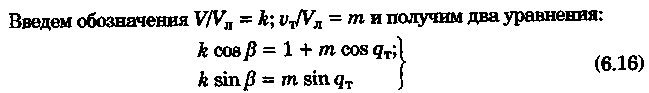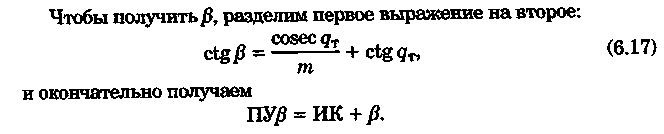








Для получения значения k возведем каждый член уравнения (6.16) в квадрат и сложим:



По формулам (6.17) и (6.18) составляются таблицы, прилагаемые к автосчислителю.
Обратная задача Даны ПУβ, Vл, Кт, и Vт. Требуется найти β, ИК и V.

Спроектируем треугольник скоростей на линию, перпендикулярную линии пути.

О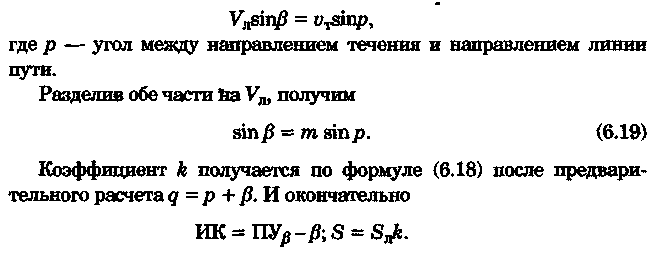бщий катет позволяет написать равенство


Иначе обе задачи могут быть решены так: в соответствии с рис. 6.16, запишем векторное уравнение сложения скоростей Vл, и vт через проекции векторов на меридиан (VNL, VNт, VN) , и параллель (VEL, vEт, VE). Тогда будем иметь следующую систему уравнений:



Иллюстрация связи векторов в координатах показана на рис. 6.19:

Тогда задачи сформулиру­ются следующим образом: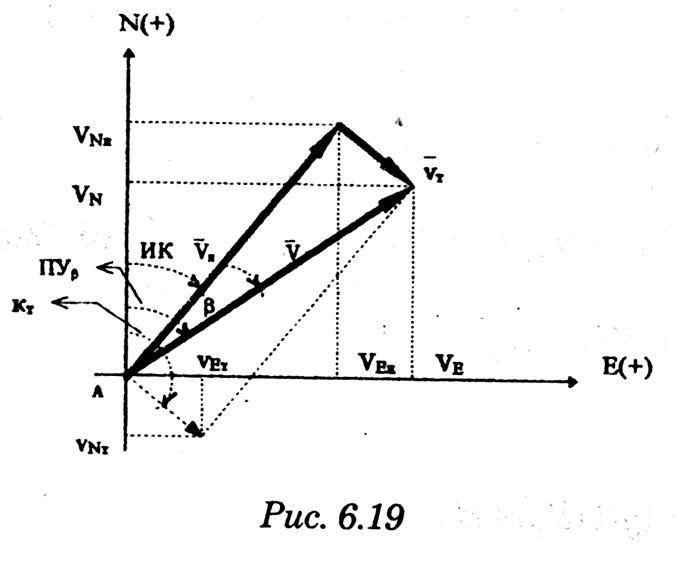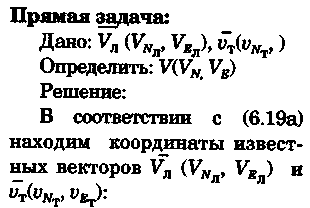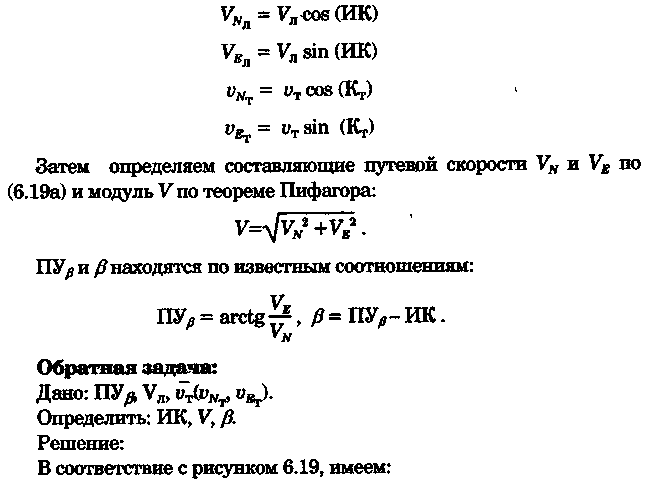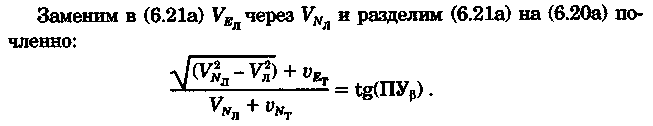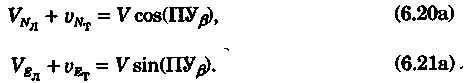














Перейдем к записи в строку, оставив в левой части выражение с радикалом а сумму известных величин обозначим через посто­янную В.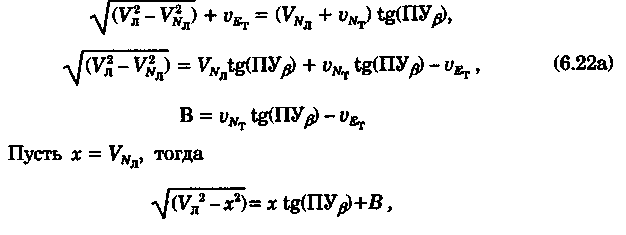



Теперь возведем обе части (6.22а) в квадрат для освобождения от квадратного корня и запишем полученное квадратное уравнение в стандартной форме:



Появление квадратного уравнения формально оправдано, из-за периодичности тригонометрической функции tg (ПУβ). Из практики известно, что для движущегося судна значение угла β обычно не ве­лико и составляет несколько градусов, а поэтому величина х должна быть близка к VN, т. е. ИК не должен намного отличаться от ПУβ. Ис­ходя из этого предположения и выбирается корень уравнения. После определения х, находим остальные неизвестные: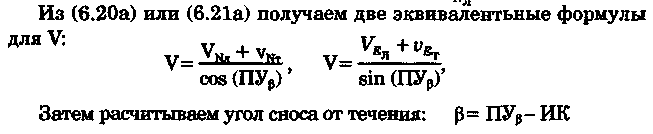




Учет приливо-отливного течения

Направление и скорость приливо-отливного течения меняются от места к месту, а также с течением времени, и поэтому при счис­лении приходится делать допуск на их постоянство на протяжении некоторого промежутка времени. За такой промежуток времени ус­ловно принимают 1 ч. В открытых морях приливо-отливные течения характеризуются малыми скоростями, замкнутыми орбитами, как правило, при ведении счисления не учитываются. Вблизи бере­гов и в узкостях приливо-отливные течения могут достигать 6...8 и даже 10 уз, и поэтому они непременно должны учитываться, осо­бенно при обратной задаче, т. е. при выборе и расчете ИК. Хотя при плавании в узкостях счисление тщательно контролируется обсерва­циями, необходимо так рассчитать ИК, чтобы предотвратить снос течением в опасные для плавания районы.

Сведения о приливо-отливных течениях помещаются непосредственно на навигацион­ных картах, в специальных атласах или приводятся в таблицах. Во всех случаях элементы течения приведены к моменту наступления полной воды в основном пункте. Поэтому для выборки данных о те­чении необходимо знать с достаточной точностью (± 30 мин) время прохождения конкретного района. Это является одной из особенно­стей учета приливо-отливного течения. В атласах и таблицах при­водят две скорости течения — сизигийную и квадратурную.

При­ближенно сизигийными считаются течения за два дня до новолуния и полнолуния и два последующих дня, квадратурными — за два дня до первой и третьей фазы Луны и два последующих дня. В осталь­ные дни течения считаются промежуточными: скорость их берется как средняя арифметическая. Для учета течений необходимо соста­вить таблицу (табл. 6.2).

П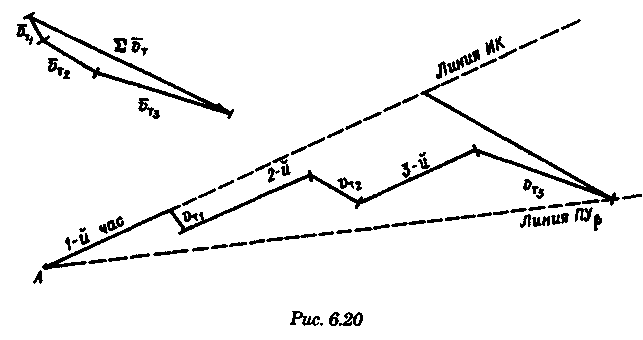ри составлении таблицы интерполяция по времени должна со­ставлять 30 мин, т. е. если, например, Тп.в = 10 ч 20 мин, то 1 ч по­сле наступления воды будет приходиться на промежуток времени от 10 ч 50 мин до 11 ч 50 мин (Tср = 11 ч 20 мин).

После того как будут найдены элементы приливо-отливного тече­ния на каждый час плавания, его учет выполняется способами, изло­женными выше. Вместо того чтобы откладывать течение каждый час, можно найти геометрическую сумму векторов течения за 2, 3, 4 ч и выполнить прокладку построением двух линий: линии ИК и линии ПУ (рис. 6.20). Аналогично можно поступить в случае обратной зада­чи, когда требуется рассчитать ИК.

При значительных скоростях течения может оказаться, что необхо­димо будет сделать второе приближение. Сделав прокладку ИК и со­ставив таблицу элементов течения, делаем прокладку линии ПУ. Ко­ординаты судна и моменты времени могут существенно отличаться от полученных при предварительной прокладке без учета течения. В этом случае корректируются элементы течения в таблице и построение ли­нии пути повторяется.

Скорость и направление временного (ветрового) течения выбира­ют из специальных карт, составленных для типовых полей ветра. Если таких пособий нет, то за основу для расчета скорости и направ­ления течения принимают сведения об истинном ветре, скорость и направление которого должны определяться 1...2 раза каждый час.

Для вычисления скорости ветрового течения, уз, используется формула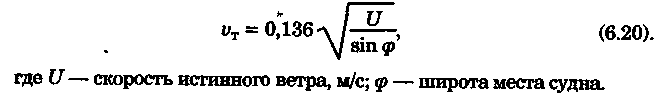



Направление ветрового течения в северном полушарии отклоня­ется вправо от направления ветра на величину около 45°, в южном полушарии — влево. В мелководных районах этот угол равен при­ближенно 25°. Время, за которое течение приобретает скорость, соот­ветствующую вычисляемой по формуле, называется временем разви­тия и зависит от широты места и глубины мора Так, при глубинах 25м ветер силой 4...5 баллов образует течение через 1...2ч, а при глубинах 250м —через 10... 12ч. При длительных ветрах скорость ветрового течения достигает 0,5...0,8уз и его необходимо учитывать при ведении счисления и при анализе невязок счисления.
Совместный учет дрейфа и течения

В практике судовождения часто случается, что течение и ветер действуют на судно одновременно. При совместном учете дрейфа и течения следует различать два случая:

известны угол дрейфа и элементы течения;

известен только суммарный угол сноса, равный алгебраической сумме с = α + β (рис. 6.21).

В 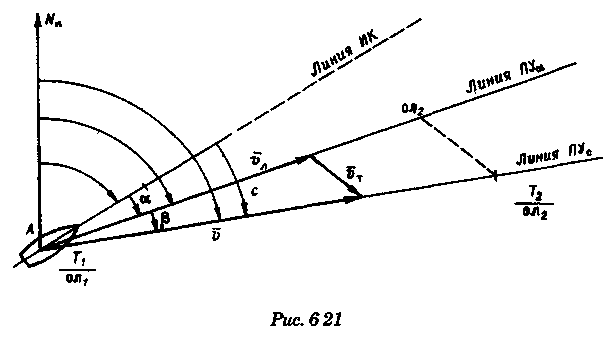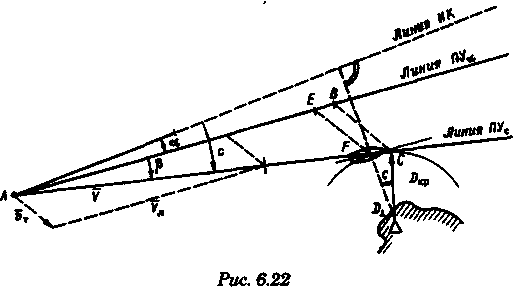первом случае при решении прямой задачи производится по­следовательный учет сначала дрейфа, а затем течения. На карте про­кладывается коротким отрезком линия ИК, затем линия ПУα, по ко­торой следовало бы судно, если бы не было течения. На ней отклады­вается вектор скорости судна по лагу Vл в выбранном масштабе (см. рис. 6.21). Из конца вектора скорости судна откладывается вектор скорости течения. Соединив начальную точку А с концом вектора те­чения, получим линию пути. При больших углах дрейфа
(α > 10°), если лаг жестко связан с корпусом судна, пройденное расстояние от­кладывается по линии ПУα и равно S = SЛ sec α.

При обратной задаче поступают наоборот. Сначала учитывают течение, затем дрейф. Для этого из начальной точки А откладывают вектор течения, из конца этого вектора радиусом, равным скорости судна по лагу, делают засечку на линии ПУс (рис. 6.22). Сняв с карты значение ПУα, рассчитывают ИК = ПУα - α.

В тех случаях, когда известен только суммарный угол сноса, на карте прокладывают две линии: линию ИК и линию пути. Счислимая точка находится перенесением точки с линии ИК на линию пути по направлению общего сноса, который должен быть предварительно определен. Если направление общего сноса неизвестно, то необходи­мо знать истинную скорость судна, например из обсерваций по РНС. Так как изменение курсов часто приурочивается к моменту прохож­дения траверза или моменту кратчайшего расстояния до объекта, следует хорошо различать эти два случая (их иллюстрирует рис. 6.22). Кратчайшее расстояние Dкр откладывается до линии ПУС, а полученная точка С переносится на линию ПУα в точку В по на­правлению, обратному направлению течения. Отрезок АВ равен Sл, пройдя его, судно окажется в точке С. При нахождении маяка на тра­верзе (D_┴) следует восстановить перпендикуляр к линии ИК (провес­ти ИП = ИК ± 90°), а затем полученную точку F следует перенести на линию ПУα в точку Е. Угол между D_┴ и Dкр будет равен углу с. Разность D_┴ и Dкр может быть обнаружена радиолокатором при углах с > 7...10°.
Навигационные методы определения пути судна

И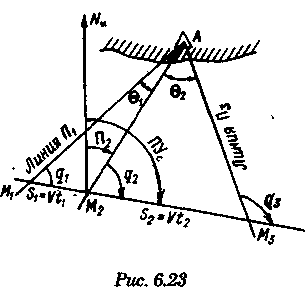зложенные методы определения угла дрейфа по пе­ленгам плавающего ориентира могут быть использованы и для нахождения суммарного угла сноса, но объект в этом случае дол­жен быть неподвижен. Кроме того, судоводителю часто не обяза­тельно знать элементы сноса ветром и течением, гораздо важнее знать элементы движения судна относительно Земли под совокуп­ным действием машины, течения, ветра и волнения. Поэтому во всех случаях, когда это возможно, штурман обязан определять элементы движения судна (путевой угол и истинную скорость) из наблюдений и принимать их в расчет при дальнейшем счислении. Наиболее надежно это можно сделать после получения ряда последовательных определений места судна по береговым ори­ентирам при постоянных курсе и скорости. Если элементы сно­са постоянны, то прямая, соеди­няющая эти точки, будет лини­ей пути, а угол между ней и ли­нией ИК — суммарным углом сноса с. В тех случаях, когда выполнить обсервацию нельзя, например в видимости находит­ся объект, положение которого не определено, можно найти линию, параллельную линии пути, а следовательно, и угол с по пеленгам неподвижного ориентира и промежуткам времени.

Пусть судно следует постоянным курсом и скоростью по линии пути (рис. 6.23), направление которой неизвестно. В произвольные, но фиксированные с точностью до секунды моменты времени взяты три пеленга П1„ П2, П3 неподвижного ориентира А. Если элементы сноса за период наблюдений постоянны, то положение линии пути будет определяться отрезками расстояний, пройденных судном за время между первым и вторым пеленгами (S1 = Vt1) и между вторым и третьим пеленгами (S2 = Vt2). Иными словами, любая прямая, пе­ресекающая все три пеленга так, что ее отрезки между пеленгами от­носятся как


будет параллельна линии пути судна.

Из рис. 6.23 видно, что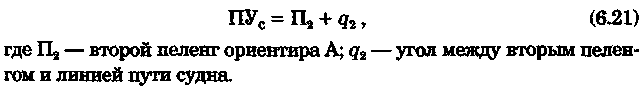



Величина П2 известна из наблюдений, а угол q2 можно вычислить по формуле, полученной при решении двух треугольников. Из тре­угольников M1AM2 и M2AM3 найдем значение АМ2: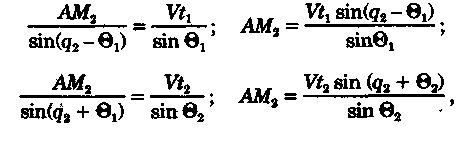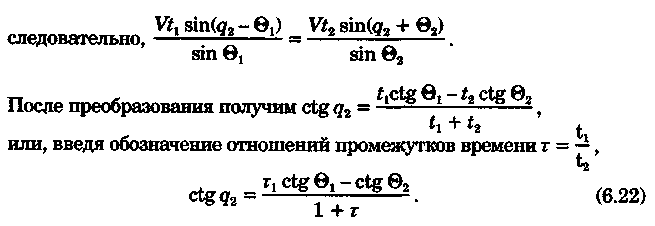




В формулу (6.22) не входит скорость судна, так как было принято, что она постоянна, поэтому путь судна может быть определен неза­висимо от того, известна ее величина или нет. Необходимо только помнить, что таким методом мы находим направление движения судна, а не линию действительного пути и место судна на ней.

Решение задачи можно упростить, если взять пеленги через рав­ные промежутки времени (t1 = t2). При
r = 1 получим



По этой формуле можно легко составить таблицу, из которой по аргументам Θ1 и Θ2 выбирается значение q2.

Данная задача может быть решена либо с помощью графиче­ских методов, изложенных в п. 6.3, либо с использованием каль­ки или линейки (рис. 6.24).

О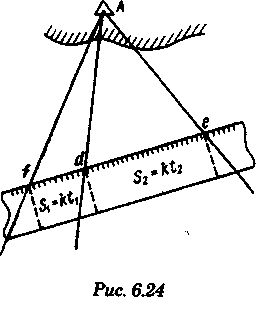тложив на кальке или линейке два отрезка S1 = kt1 и S2 = kt2 (где k — произвольный коэффициент) или же плавание по лагу S1 и S2, накладываем кальку (линейку) на проложенные на карте линии пеленгов и, двигая ее, находим такое положение, при котором точки f, d, e будут лежать соответ­ственно на первом, втором и треть­ем пеленгах. Прямая, проведенная через эти точки, будет параллельна линии пути судна. Для повышения точности все графические построе­ния рекомендуется делать в воз­можно более крупном масштабе. Основное достоинство этого способа заключается в том, что путь можно определить по любому неподвижно­му ориентиру (буй, маяк, камень, дерево, вершина) независимо от то­го, нанесен он на карту или нет.

Рассмотрим основные источники погрешностей при определе­нии суммарного угла сноса по пеленгам неподвижного ориентира.

Погрешностями в отсчетах времени t1 и t2 при использовании се­кундомера можно пренебречь.

В погрешности поправки компаса, как видно из формул для расчета q2, входят только углы Θ1 и Θ2, представляющие собой разности пеленгов. Поэтому систематическая погрешность при­нимаемой поправки компаса на вычисление угла q2 влияния не оказывает.

При определении ПУС = П2 + q2, если пеленг будет содержать погрешность в поправке компаса ε∆k, то полученное направление пути также будет содержать эту погрешность. На определение сум­марного угла сноса эта погрешность влиять не будет, так как полу­ченные ПУС и ИК будут ошибочными на одну и ту же величину ε∆k, а угол сноса определяется как разность ПУС - ИК = с.

Случайные погрешности пеленгования скажутся при расчете q2, так как углы Θ1 и Θ2 рассчитываются по значениям пеленгов.

Расчеты показывают, что при достаточно больших углах Θ1, Θ2 и mп = ± 0,3° случайные погрешности в определении угла q2 находятся в пределах ± 1°. Практические наблюдения подтверждают этот вывод.

Если за время наблюдений элементы сноса могут измениться, рас­смотренным способом пользоваться не следует.