Вопрос №11. Элементы счисления и их характеристика. Прокладка при отсутствии дрейфа и течения. Счислением координат судна (счислением)

• Название: Элементы счисления и их характеристика. Прокладка при отсутствии дрейфа и течения. Счислением координат судна (счислением)
• Анкор: Вопрос №11.doc
• Дата: 28.05.2018
• Размер: 0.55 Mb.
• Имя файла: Вопрос №11.doc
• Тип: Документы; #19730
• страница: 4 из 4

Точность графического счисления

Возможные погрешности в значениях элементов счисления, угла дрейфа, поправок компаса и лага, а также погрешности графических построений на карте, постепенно накапливаясь, приводят к тому, что действительное место судна не совпадает с нанесенным на карту. Штурман должен уметь произвести оценку точности графического счисления. Будем считать, что все погрешности малы, тогда их мож­но разбить на две группы:

погрешности, допущенные при определе­нии пути судна, и

погрешности, допущенные при расчете пройденно­го расстояния (погрешностями графических построений пренебрега­ем ввиду их малости).

Н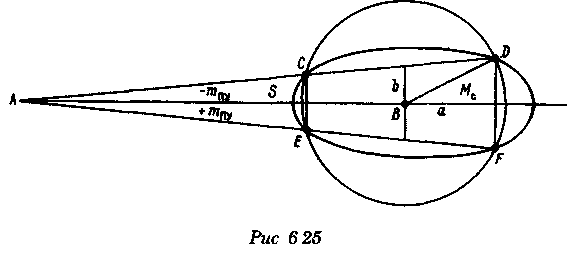а рис. 6.25 показано перемещение судна из точки А в точку В. Погрешности первой группы вызовут смещение на величину b, по­грешности второй группы вызовут смещение на величину а. Вели­чины а и b будут являться средними квадратичными продольными и поперечными погрешностями счисления, так как они вызваны средними и квадратичными погрешностями mпу, m∆л и ms. Зная значения а и b, можно вычислить величину Мс — среднюю квадратичную погрешность счисления. При больших разностях а и b площадь возможного нахождения места судна будет характеризо­ваться эллипсом с полуосями а и b, который можно от руки описать вокруг фигуры CDEF.

В общем виде значение b равно:



где mпу —средняя квадратичная погрешность путевого угла, град.

При отсутствии дрейфа и течения m = mк —средней квадратичной погрешности курса. Для гирокомпаса mк = 1...1,5°. При учете дрейфа эта погрешность квадратически складывается со средней квадратич­ной погрешностью в учете дрейфа α, которая может достигать значе­ния α/3. При наличии течения средняя квадратичная погрешность в учете угла сноса от течения mβ =f(V, mv, p, vт) и может достигать не­скольких градусов. Целесообразно учитывать ее максимальное значе­ние. Величина α зависит от погрешностей в принятом значении по­правки лага, а также от погрешностей в пройденном расстоянии, вы­званных неучетом течения или учетом недостоверного течения.

Можно написать, что



Для случая, когда течение отсутствует, формула для Мс будет иметь вид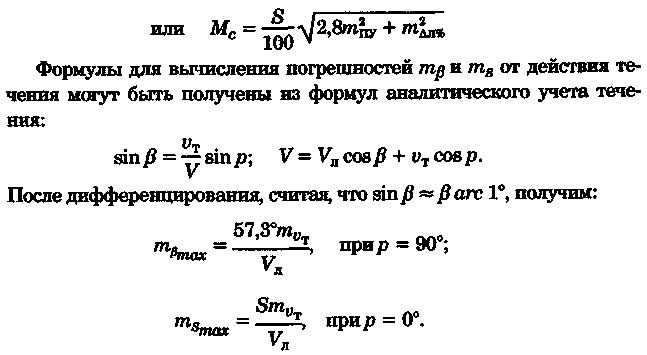




Среднее значение скорости неизвестного течения принимается равным: при плавании в районах со значительными приливо-отлив­ными течениями 0,5... 1,0уз; в районах открытого моря, где, по дан­ным пособий, течение отсутствует, 0,3...0,5уз; в прибрежной зоне 0,2...0,3 уз; ветровое течение обычно не превышает 0,3 уз.

На основании многолетних наблюдений получены следующие приближенные значения радиуса Мс для нормальных условий пла­вания в зависимости от пройденного расстояния: без ветра и течения MC = 0.02S; с учетом дрейфа Мс = 0.03S; с учетом дрейфа и течения Мс = (0,03...0,07)S.

При плавании переменными курсами решение задачи по оценке точности счислимого места в конечной точке сводится к расчету М для каждого курса и их квадратичного суммирования (рис. 6.26):


г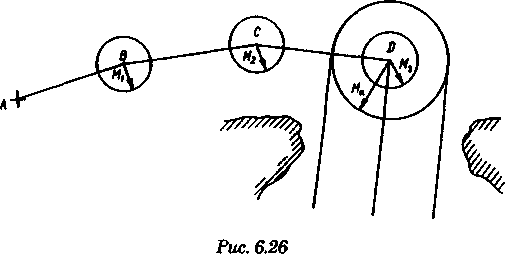де Мк — средняя квадратичная погрешность счисления в конечной точке; М1, М2, Мi — средние квадратичные погрешности на каждом курсе.

Единственной независимой переменной при оценке точности счисления надо считать время, а все другие параметры, определяю­щие точность счисления, — его случайными функциями.

Е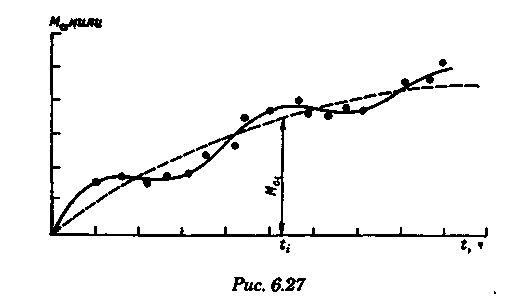сли в течение ряда рейсов по одному маршруту собрать данные о невязках и по ним построить график точности счисления в зависи­мости от времени (рис. 6.27), то осреднение всех полученных точек позволит получить согласную кривую, близкую к параболе и описы­ваемую уравнениями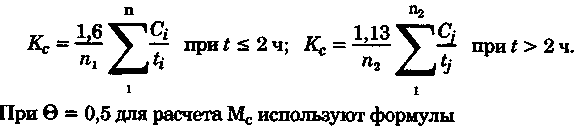



При вычислении Кc нельзя использовать невязки, полученные при недостаточно достоверных определениях места судна.

Коэффициент счисления может быть предвычислен априорно по формуле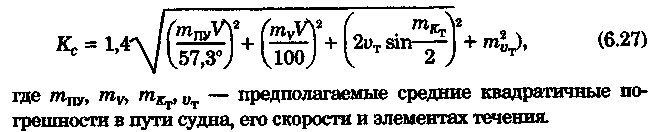



Если после длительного перехода потребуется рассмотреть воз­можность прохода какого-либо пролива по счислению, необходимо проложить три вероятных линии курса: из двух точек окружности Мк (см, рис. 6.26) и точки D. До получения надежной обсервации следует вести такую «тройную» прокладку, причем для получения вероятно­сти Р = 99,0%, соответствующей предельной погрешности, следует взять Мк, увеличенную в 3 раза

Рассмотренные формулы для оценки точности не могут га­рантировать надежность результата, они позволяют штурману только ориентировочно оценить возможные погрешности счис­ления. Поэтому следует периодически осуществлять контроль счисления, используя для этого все имеющиеся в распоряжении судоводителя средства.

В зависимости от допустимой погрешности счислимого места для конкретных условий плавания можно рассчитать необходимую пе­риодичность выполнения обсерваций: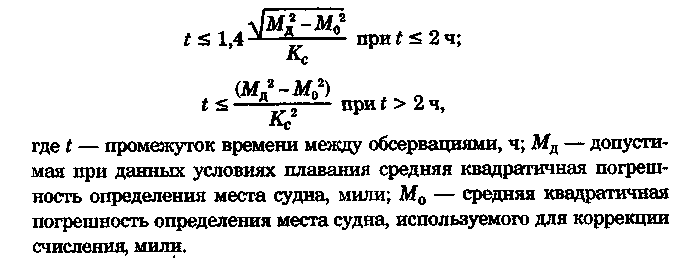


Основные формулы аналитического счисления

Кроме графического счисления, учет движения судна может про­изводиться по формулам аналитическим методом.

Аналитическим счислением называется вычисление приращений к исходным коор­динатам, обусловленным движением судна, с помощью которых оп­ределяются счислимые координаты на заданный момент времени.

Аналитическое счисление может быть табличным, когда задачи счисления решают с использованием таблиц и автоматизированным, когда решение получают с помощью вычислительных машин. Анали­тическое счисление применяется при плавании вдали от берегов на океанских переходах, когда ведение прокладки на картах мелкого масштаба становится неточным из-за больших погрешностей графиче­ских построений. Кроме того, аналитическое счисление применяется при решении астрономических задач, когда вычисляются координаты счислимых мест. Оно может применяться при вычислении обсервованных координат при разновременных линиях положения для при­ведения наблюдений к одному моменту и, наконец формулы аналити­ческого счисления заложены во все автоматические счислители коор­динат и путепрокладчики.

Получим основные формулы аналитического счисления. Предпо­ложим, что судно находилось в точке отшествия А (рис. 7.1) с извест­ными координатами φ1, λ1 и, следуя постоянным курсом по локсодро­мии, пришло в точку пришествия В с координатами φ2, λ2. Если будут известны сделанные судном РШ и РД, то координаты точки В легко получить из соотношений



Значения РШ и РД, входящих в эти формулы, можно рассчитать по известным элементам движения:
К — курсу судна и S — расстоя­нию, пройденному судном. Для вывода основных зависимостей обра­тимся к элементарному треугольнику Аа’Ь' (см. рис. 7.1), считая Землю за сферу.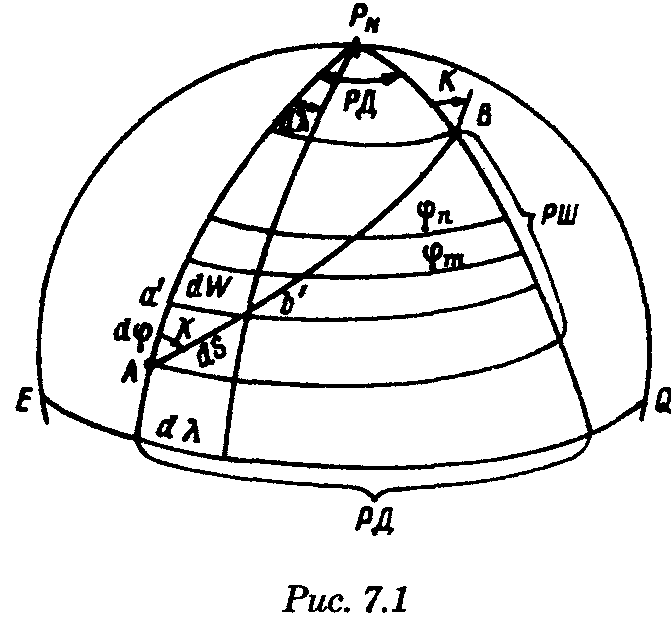






Геометрический смысл состоит в том, что ОТШ представляет собой длину отрезка параллели не­которой промежуточной широ­ты φn, заключенной между ме­ридианами пункта отхода и пункта прихода. Единицей из­мерения отшествия является морская миля.

Для вычисления РД вос­пользуемся известным соот­ношением между длиной дуги экватора и параллели:






Таким образом, отшествие ω, вычисленное по формуле (7.2), представляет собой длину параллели в морских милях между мери­дианами точек А и Б в промежуточной широте, которая определяется соотношением



На практике при ведении аналитического учета на коротких рас­стояниях можно положить, что в интервале от φ1 до φ2 значение cosφ изменяется линейно, тогда



и приближенная формула для вычисления РД будет иметь вид



Разность между средней параллелью с широтой φm и промежу­точной φn показана на рис. 7.1.

П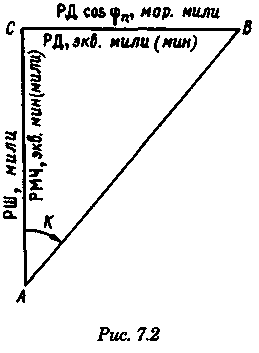о формулам (7.1) и (7.2) составлена табл. 24 «Разности широт и отшествия», помещенные в МТ-75. В ней по пройденному рас­стоянию от 0 до 100 миль и курсу через 1° можно получить гото­вые значения РШ и ОТШ. Курсы первой четверти (NE) выделены и напечатаны жирным шрифтом, а рядом даны три курса осталь­ных четвертей, которым соответствуют синусы и косинусы первой четверти. Значения РШ и ОТШ даны в таблице до сотых долей мили и поэтому могут быть исполь­зованы с достаточной точностью для плаваний в 10 и 100 раз больших чем S. Таблица дает решение прямо­угольного треугольника по гипотену­зе и прилежащему к ней углу; она может применяться также для реше­ния различных других задач, ос­нованных на соотношениях, свя­зывающих элементы прямоугольного треугольника на меркаторской карте (рис. 7.2).

В МТ-75 помещена также специаль­ная таблица для нахождения разности долгот (табл. 25-а), составленная по формуле РД = ОТШ sec φm. Если в таблицу войти с приближенным значением



то получится приближенная величина РД, если с точным значе­нием qn, то получится точное значение РД (принимая Землю за шар). В этой таблице даны результаты вычислений для отшествия в 1, 2,..., 9 и 100 миль и для широт от 0 до 90°.

Чтобы получить РД двух пунктов для десятков или сотен миль отшествия, просто переносят запятую, отделяющую целую часть от дробной в найденных табличных значениях. Для учета сфероидичности Земли при ведении аналитического счисления составлены табл. 25-b «Коэффициенты для учета сфероидичности Земли при счислении пути корабля». В атом случае надо пользоваться средней широтой.

Использование аналитического счисления в судовождении

Табличное аналитическое счисление принято подразделять на три вида: простое, составное и сложное.

Простое аналитическое счисление выполняется, когда судно сле­дует одним курсом. В этом случае по формулам или таблицам вычис­ляют РШ и РД и получают конечные координаты. Порядок решения задачи будет следующий.

1. 
   Пусть φ1 и λ1— координаты начальной точки;
   

ИК — истинный курс, которым шло судно,

S — пройденное расстояние по курсу от начальной точки до точки пришествия в морских милях.

Необходимо найти координаты точки пришествия. Из табл. 24 МТ-75 по аргумен­там ИК и S выбираем РШ и ОТШ.

Если S более 100 миль, то его значение разделяют на несколько слагаемых, равных или менее 100 миль каждое, для которых и выбирают значение РШ и ОТШ. При наличии дрейфа вместо ИК аргу­ментом для входа в таблицу служит ПУ=ИК + α. При дробном зна­чении ИК (ПУа) необходимо произвести интерполяцию.

2. Рассчитывается средняя широта (с точностью до 0,1°);



3. По аргументам φm и ОТШ из табл. 25-а МТ-75 выбирается РД.

4. При необходимости учесть сфериодичность Земли выбираются значения коэффициентов f и g из табл. 25-6 по аргументам: для f по φm, для g по φm и РШ. Вычисляются поправочные члены ∆φ и ∆λ, которыми исправляются начальные значения РШ и РД:



5. Вычисляются координаты точки пришествия φ2 и λ2по формулам



Если возникает необходимость по известным координатам точки отшествия и точки пришествия вычислить курс и расстоя­ние между точками, то целесообразно использовать формулы



Для отсчета отшествия по РД можно применить формулы: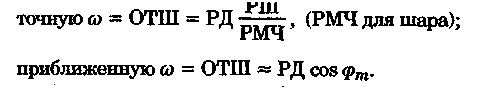

Составным счислением, будет называться счисление, когда судно совершает плавание несколькими курсами, но штурману не нужно знать координаты всех промежуточных точек, а необходимо лишь вычислить координаты точки пришествия. В этом случае следует подсчитать алгебраическую сумму разностей широт на каждом от­дельном курсе, называемую генеральной разностью широт (Ген РШ) и алгебраическую сумму отшествий, называемую гене­ральным отшествием (Ген ОТШ) (рис. 7.3):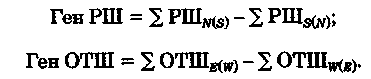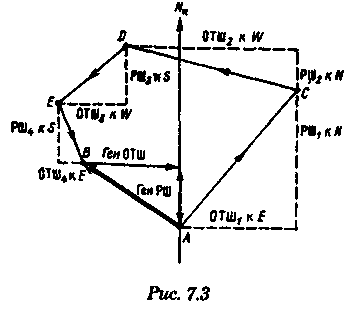



РД находится из табл. 25-а по аргументам φm и Ген ОТШ. Коор­динаты точки пришествия найдутся из соотношений: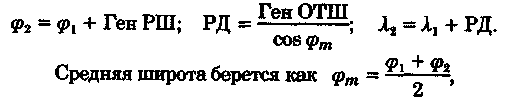



т. е. предполагается, что все отдельные отшествия сделаны на одной и той же широте φm. Такое допущение для большинства практических случаев заметных ошибок не дает. Бели же необходимо исключить по­грешность от замены промежуточной широты средней широтой, то следует воспользоваться сложным счислением.

Сложным счислением называется такое счисление, при котором для каждого курса в точке поворота рассчитываются не только РШ и ОТШ, но и РД. Алгебраическая сумма РД называется генераль­ной разностью долгот (ГенРД):



Курс, рассчитанный по Ген РШ и Ген ОТШ, ведущий непосредст­венно в точку пришествия, называется генеральным курсом, а расстояние по генеральному курсу между этими точками называется генеральным плаванием.

Метод составного (сложного) счисления позволяет вести учет по­стоянного и приливо-отливного течения, а также учет циркуляции.

При учете течения его направление принимается за отдельный до­полнительный курс, а произведение скорости течения на время его действия — за плавание. По этому отдельному курсу выбирают РШ и ОТШ. При учете циркуляции за курс судна принимается промежуточ­ный курс ИКпр = ИK1 + q, а за плавание — величина d (плавание по промежуточному курсу на циркуляции).
Точность аналитического счисления

Аналитическое вычисление координат по формулам или табли­цам исключает погрешности графических построений на карте, но не исключает влияния погрешностей в поправках компаса или лага, влияния погрешностей, вызванных учетом дрейфа и течения. Поэто­му все, что было сказано выше о точности графической прокладки, полностью относится и к аналитическому счислению. Среднюю квад­ратичную погрешность счисления можно вычислить по формуле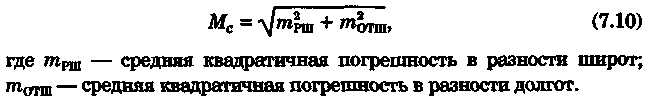



Обе эти погрешности зависят от погрешностей курса (mик) или путевого угла (mпу), а также от погрешности в пройденном расстоя­нии (ms) и получаются путем дифференцирования основных фор­мул (7.1) и (7.2):



Кроме того, на точность аналитического счисления могут оказы­вать влияние погрешность от замены промежуточной широты φn средней φm и погрешность от пренебрежения учетом сфероидичности Земли.

Погрешность долготы, обусловленная заменой промежуточной широты средней арифметической широтой, выражается формулой



Расчеты по этой формуле показывают, что для ω = 100 миль и разности широт 8° на широтах до 50° погрешность долготы не пре­вышает 1'. При плавании в высоких широтах замена промежуточной широты средней допускается при S < 100 миль.

Для учета сфероидичности Земли при аналитическом счислении следует воспользоваться табл. 25-b МТ-75. Для вычисления ∆φ и ∆λ с учетом сфероидичности Земли, служат формулы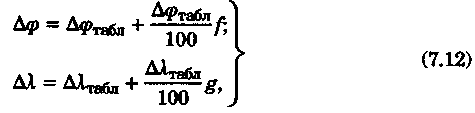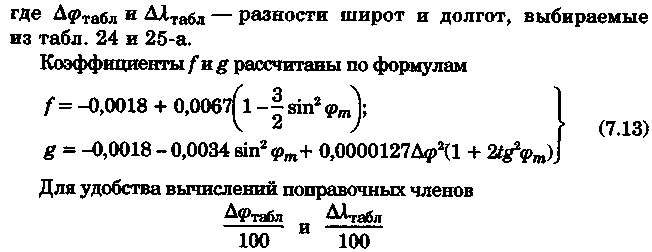





коэффициенты f и g, приведенные в табл. 25-b МТ-75, увеличены в 100 раз. Аргументами для входа в табл. 25-b служат: для получе­ния коэффициента f— средняя широта φm, для получения коэф­фициента g — средняя широта φm и разность широт ∆φ.

Практика мореплавания обязывает вахтенного штурмана ис­пользовать любую возможность для определения места судна и на основе выполненного анализа счисления и обсервации докладывать капитану о необходимости изменения курса и переноса счисления в обсервованную точку. Вопрос о коррекции счисления должен при­ниматься на основе штурманского правила: «Считай себя ближе к опасности».