элементы тригонометрии в учебниках геометрии. текст. Элементы тригонометрии в школьных учебниках геометрии Сл. 2 Историческая справка
 Скачать 200.5 Kb. Скачать 200.5 Kb.
|
|
Элементы тригонометрии в школьных учебниках геометрии Сл.2 Историческая справка Слово «тригонометрия» состоит из двух греческих слов: «тригонон» — треугольник и «метрайн» — измерять. В буквальном смысле «тригонометрия» означает «измерение треугольников». Сл.3 Тригонометрии в школе уделяется много внимания: сначала – в курсе геометрии, затем – в курсе алгебры и начал анализа. Сл.4 Первое знакомство с тригонометрическими функциями углового аргумента в геометрии. Значение аргумента рассматривается в промежутке (0°;90°). На этом этапе учащиеся узнают, что sinα, сosα, tgα и ctgα угла зависят от его градусной меры, знакомятся с табличными значениями, основным тригонометрическим тождеством и некоторыми формулами приведения. Сл.5 Решающую роль в решении задач на тригонометрию играет знание определений тригонометрических функций. Важно понимать, что тригонометрические функции — это безразмерные величины (не имеют единиц измерения), они показывают только отношение. Сл.6 ЗНАЧЕНИЯ ТРИГОНОМЕТРИЧЕСКИХ ФУНКЦИЙ: Таблица основных значений тригонометрических функций предлагает значения sinα, cosα, tgα и ctgα от нескольких углов: 0°, 30°, 45°, 60°, 90°. В учебнике А. В. Погорелова понятие косинуса угла используется при доказательстве теоремы Пифагора, а в учебнике Л. С. Атанасяна и др. теорема Пифагора к этому времени уже доказана и доказательство её основано на понятиях площади квадрата и прямоугольника. Сл.7 Основное тригонометрическое тождество — это следствие из теоремы Пифагора для тригонометрического круга. Рассмотрим треугольник ABC. Запишем теорему Пифагора для него: Поделим каждое слагаемое на AB2. Первое и второе слагаемые — это квадраты синуса и косинуса для угла A или B. Из основного тригонометрического тождества при наличии значения одной из функций — sin или cos — можно найти вторую. Сл.8 Формулы для тангенса и котангенса. 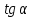 = = 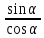 и ctgα = и ctgα = 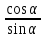 Сл. 9 На втором этапе: Обобщение понятий синуса, косинуса, тангенса и котангенса для углов (0°;180°). На этом этапе рассматривается взаимосвязь тригонометрических функций и координат точки на плоскости, доказываются теоремы синусов и косинусов, рассматривается вопрос решения треугольников с помощью тригонометрических соотношений. Сл.10 Сл.11 В учебнике Л. С. Атанасяна доказательство теоремы косинусов основано на координатном методе. В учебнике А. В. Погорелова на векторном методе. Сл.12 Теорема синусов эффективна тогда, когда заданы два угла и сторона треугольника, теорема косинусов используется, если заданы две стороны и угол между ними. Сл.12 Рассмотрим как используется изложение тригонометрии в действующих учебниках геометрии А. В. Погорелова и Л. С. Атанасяна. В учебнике А. В. Погорелова изложение тригонометрических функций осуществляется методом дедукции, а в учебнике Л. С. Атанасяна – индукции. причем в первом учебнике наблюдается связь изложения тригонометрических функций с изложением геометрического материала, тогда как во втором учебнике применение тригонометрических функций к обоснованию геометрических зависимостей более ограничено, чем в первом. Сл.14-16. Сравнительный анализ тригонометрических тем учебников 8-9 класса. Мы видим что в учебнике Погорелова тригонометрии отведено больше тем чем в учебнике Атанасяна. Сл.17 От введения тригонометрии в курс геометрии будет зависеть, насколько успешным будет изучение тригонометрии в курсе алгебры. Надо прийти к пониманию того, что тригонометрия в геометрии и тригонометрия в алгебре не являются никак не связанными отдельными дисциплинами, это – единый блок, изучение которого невозможно без получения первоначальных сведений о тригонометрии в курсе геометрии. К тому же в результате начавшейся реформы тригонометрический материал, который ранее изучался в курсе IX класса, был перенесен в X класс алгебры и начало анализа. Поэтому на сегодняшний день те учащиеся, которые не пожелали учиться в старшей школе, знакомятся с этой темой только в курсе геометрии. Это налагает еще большую ответственность на изучение первоначальных тригонометрических сведений в курсе геометрии. |
