Математика. Матан2.0. Если функция uf(x,y) имеет непрерывные смешанные производные высших порядков, то справедливо соотношение
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
; ; ; 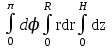 ; ;   : :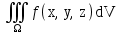 к сферическим координатам имеет вид: к сферическим координатам имеет вид: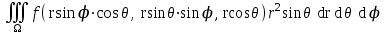 ; ; ; ; ; ; ; ;  ; ; ; ; ; ; ; ; . . ; ;  ; ;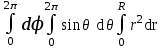 ; ;  ; ;  . . ; ;  ; ;  . . ; ;  ; ; 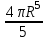 . .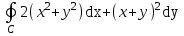 . Вычислить . Вычислить . .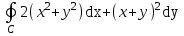 . Вычислить . Вычислить . .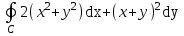 . Вычислить . Вычислить - - . . . Вычислить . Вычислить . . . Вычислить . Вычислить . . . Вычислить . Вычислить - -  . . ; ;  ; ;  ; ;  ; ; . . ; ; ; ;  ; ;  ; ;  . .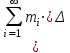 хi; хi;  хi; хi; хi; хi;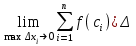 хi хi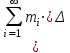 хi хi хi хi  ; ;  равен: равен: ; ;  ; ;  ; ; 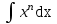 равен: равен: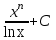 ; ; 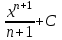 ; ;  ; ;  . . . . ; ; 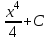 ; ; 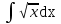 . . ; ;  ; ;  ; ;  ; ;  . . . . cos2x + C; cos2x + C;  cos2x + C; cos2x + C;  . . ; ; ; ; ; ;  ; ;  . . равен: равен: ; ;  ; ;   ; ; 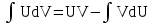 ; ; ; ;  ; ; 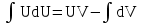  равен: равен: ; ;  ; ; 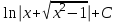 ; ; . . 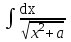 равен: равен: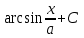 ; ;  ; ; ; ;  ; ;  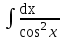 равен: равен: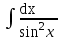 равен: равен: ? ? . . ? ? . . ? ? . .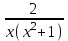 на элементарные дроби имеет вид: на элементарные дроби имеет вид: ; ;  ; ;  ; ; 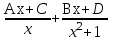 ; ;   на элементарные дроби имеет вид: на элементарные дроби имеет вид: ; ;  ; ;  ; ;  ; ; 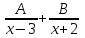 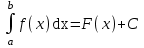 ; ; 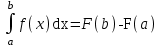 ; ; ; ; |
