|
Математика. Матан2.0. Если функция uf(x,y) имеет непрерывные смешанные производные высших порядков, то справедливо соотношение
Если кривую интегрирования AB разбивать на части AC и CB, то
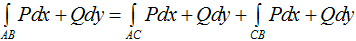
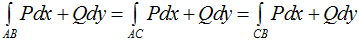
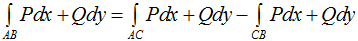
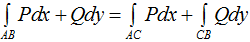
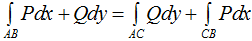
![]()
При изменении направления на кривой интегрирования криволинейный интеграл I рода:
не изменяется
требует перемены местами x и y
требует перемены местами P и Q
становится равным нулю
изменяет свой знак
По формуле 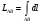 вычисляется: вычисляется:
Длина дуги AB плоской или пространственной линии
Площадь фигуры, расположенной в плоскости xOy и ограниченной замкнутой линией
Масса материальной дуги AB
Работа, совершаемая силой 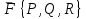 , действующей на точку при перемещении ее по дуге AB , действующей на точку при перемещении ее по дуге AB
Аппликата центра тяжести C дуги AB
По формуле 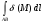 вычисляется: вычисляется:
Масса материальной дуги AB
Площадь фигуры, расположенной в плоскости xOy и ограниченной замкнутой линией
Длина дуги AB плоской или пространственной линии
Работа, совершаемая силой 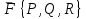 , действующей на точку при перемещении ее по дуге AB , действующей на точку при перемещении ее по дуге AB
Аппликата центра тяжести C дуги AB
По формуле 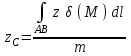 вычисляется: вычисляется:
Аппликата центра тяжести C дуги AB
Ордината центра тяжести C дуги AB
Абсцисса центра тяжести C дуги AB
Работа, совершаемая силой 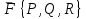 , действующей на точку при перемещении ее по дуге AB , действующей на точку при перемещении ее по дуге AB
Масса материальной дуги AB
По формуле 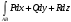 вычисляется: вычисляется:
Работа, совершаемая силой 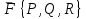 , действующей на точку при перемещении ее по дуге AB , действующей на точку при перемещении ее по дуге AB
Длина дуги AB плоской или пространственной линии
Площадь фигуры, расположенной в плоскости xOy и ограниченной замкнутой линией
Масса материальной дуги AB
Аппликата центра тяжести C дуги AB
Двойной интеграл  с положительной подынтегральной функцией может быть истолкован физически как: с положительной подынтегральной функцией может быть истолкован физически как:
масса соответствующей пластины;
объём соответствующей пластины;
объём соответствующего цилиндроида;
масса соответствующего цилиндроида;
нет верного ответа.
Двойной интеграл  с неотрицательной подынтегральной функцией может быть истолкован геометрически как: с неотрицательной подынтегральной функцией может быть истолкован геометрически как:
объём соответствующего цилиндроида;
объём соответствующей пластины;
масса соответствующей пластины;
масса соответствующего цилиндроида;
длина дуги кривой
Двойной интеграл  в полярных координатах имеет вид: в полярных координатах имеет вид:
 ; ;
 ; ;
 ; ;
 ; ;

Тройным интегралом от функции f(x, y) по области называется:
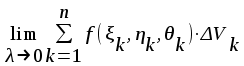 ; ;
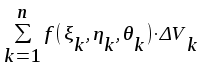 ; ;
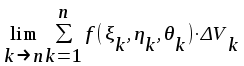 ; ;
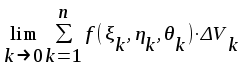 ; ;
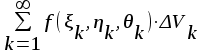
Тройной интеграл 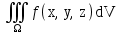 с положительной подынтегральной функцией может быть истолкован физически как: с положительной подынтегральной функцией может быть истолкован физически как:
масса соответствующего тела;
объём соответствующего тела;
объём соответствующего цилиндроида;
масса соответствующей пластины;
плотность соответствующего тела
Формула преобразования тройного интеграла 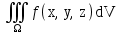 к цилиндрическим координатам имеет вид: к цилиндрическим координатам имеет вид:
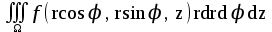 ; ;
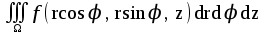 ; ;
 ; ;
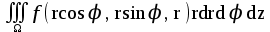 ; ;

Двойной интеграл  с положительной подынтегральной функцией может быть истолкован физически как: с положительной подынтегральной функцией может быть истолкован физически как:
масса соответствующей пластины;
объём соответствующей пластины;
объём соответствующего цилиндроида;
масса соответствующего цилиндроида;
нет верного ответа.
Двойной интеграл  с неотрицательной подынтегральной функцией может быть истолкован геометрически как: с неотрицательной подынтегральной функцией может быть истолкован геометрически как:
объём соответствующего цилиндроида;
объём соответствующей пластины;
масса соответствующей пластины;
масса соответствующего цилиндроида;
длина дуги кривой
Двойной интеграл  в полярных координатах имеет вид: в полярных координатах имеет вид:
 ; ;
 ; ;
 ; ;
 ; ;

Тройным интегралом от функции f(x, y) по области называется:
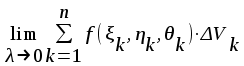 ; ;
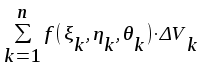 ; ;
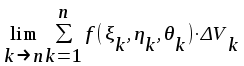 ; ;
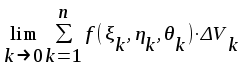 ; ;
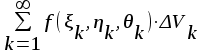
Тройной интеграл 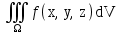 с положительной подынтегральной функцией может быть истолкован физически как: с положительной подынтегральной функцией может быть истолкован физически как:
масса соответствующего тела;
объём соответствующего тела;
объём соответствующего цилиндроида;
масса соответствующей пластины;
плотность соответствующего тела
Формула преобразования тройного интеграла 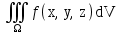 к цилиндрическим координатам имеет вид: к цилиндрическим координатам имеет вид:
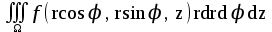 ; ;
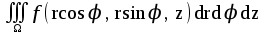 ; ;
Сумма членов бесконечной числовой последовательности u1, u2, …, un, … или u1 + u2 + … + un + … =  un называется: un называется:
числовым рядом
частичной суммой
степенным рядом
функциональным рядом
сходящимся рядом
Суммы Sn = u1 + u2 + …+ un =  uk, n = 1, 2 называются: uk, n = 1, 2 называются:
частичными суммами
суммами сходящегося ряда
суммами расходящегося ряда
суммами и разностями этих рядов
функциональным рядом
Предел последовательности частичных сумм limSn= S, S =  un называется: un называется:
суммой расходящегося ряда
суммой сходящегося ряда
частичной суммой
числовым рядом
сходящимся рядом
Ряд  (un + vn), где элементы получены в результате сложения исходных элементов с одинаковыми номерами, называется: (un + vn), где элементы получены в результате сложения исходных элементов с одинаковыми номерами, называется:
суммой рядов
разностью рядов
произведением рядов
частным рядов
сходящимся рядом
Для того, чтобы последовательность а1, а2, … , аn была сходящейся, необходимо и достаточно, чтобы для любого Е > 0 существовал такой номер N, что при n>N и любом p> 0, где p – целое число, выполнялось бы равенство: │an+p - an│
Коши
Даламбера
Лейбница
Вейерштрасса
Абеля
Выберитегармоническийряд:

 Может быть Может быть


Для сходимости ряда  unc неотрицательными членами необходимо и достаточно: unc неотрицательными членами необходимо и достаточно:
чтобы частичные суммы ряда были неограниченными
чтобы частичные суммы ряда были четными
чтобы частичные суммы ряда были нечетными
чтобы частичные суммы ряда были ограниченными
чтобы частичные суммы ряда были знакопеременными
Если для ряда  un с положительными членами существует такое число g< 1, что для всех достаточно больших n выполняется неравенство un с положительными членами существует такое число g< 1, что для всех достаточно больших n выполняется неравенство  g, то ряд g, то ряд  uncходится, если же для всех достаточно больших n выполняется условие uncходится, если же для всех достаточно больших n выполняется условие  , то ряд , то ряд  un расходится. Это признак сходимости: un расходится. Это признак сходимости:
Коши
Лейбница
Даламбера
Вейерштрасса
Абеля
Если для ряда  un с неотрицательными членами существует такое число g< 1, что для всех достаточно больших n выполняется неравенство un с неотрицательными членами существует такое число g< 1, что для всех достаточно больших n выполняется неравенство  g, то ряд g, то ряд  un сходится, если же для всех достаточно больших n выполняется неравенство, то ряд un сходится, если же для всех достаточно больших n выполняется неравенство, то ряд  un расходится. Это признак сходимости: un расходится. Это признак сходимости:
Коши
Даламбера
Вейерштрасса
Лейбница
Абеля
Если существует предел limn→∞  = p, то при p<1 ряд сходится, а при p>1 ряд: = p, то при p<1 ряд сходится, а при p>1 ряд: 
расходится
сходится
остается без изменения
ни расходится, ни сходится
сходится частично
Укажите общегармонический ряд:





Еслиузнакочередующегосярядаu1 – u2 + u3 – u4 + … + (-1)n+1un + … абсолютные величины u1 убывают u1>u2>u3> … и общий член стремится к нулю un→0, то ряд сходится. Это признак сходимости:
Лейбница
Коши
Даламбера
Вейерштрасса
Абеля
Если сходится ряд  │un│, то этот ряд │un│, то этот ряд  un называется: un называется:
абсолютно сходящимся
абсолютно расходящимся
отрицательным рядом
положительным рядом
условно сходящимся
Если существует предел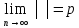 , то при p<1 ряд , то при p<1 ряд  un будет абсолютно сходящимся, а при p>1 ряд будет расходящимся. При p=1 признак не дает ответа о сходимости ряда. Это признак сходимости: un будет абсолютно сходящимся, а при p>1 ряд будет расходящимся. При p=1 признак не дает ответа о сходимости ряда. Это признак сходимости:
Коши
Даламбера
Вейерштрасса
Лейбница
Абеля
Для абсолютной сходимости ряда  un необходимо и достаточно, чтобы его можно было представить в виде: un необходимо и достаточно, чтобы его можно было представить в виде:
суммы двух сходящихся рядов с неотрицательными членами
разности двух сходящихся рядов с неотрицательными членами
произведения двух сходящихся рядов с неотрицательными членами
знакопеременного ряда
ряда с неотрицательными членами
Если членами ряда являются не числа, а функции от х, то ряд называется:
сходящимся
функциональным
положительным
отрицательным
знакопеременным
Функция Sn (X) =  (x), n = 1, 2 функционального ряда (x), n = 1, 2 функционального ряда  (х) называется: (х) называется:
знакопеременной суммой
интегральной суммой
частичной суммой
суммой сходящегося ряда
суммой расходящегося ряда
Совокупность всех значений х, для которых сходится ряд  (х) называется: (х) называется:
суммой ряда
разностью ряда
областью сходимости ряда
произведением ряда
частным ряда
Ряд  (х) сходится равномерно и притом абсолютно на отрезке [a, b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами М1 + М2 + … + Мn… т.е. имеет место неравенство │un (x)│≤ Mn. Это признак равномерной сходимости: (х) сходится равномерно и притом абсолютно на отрезке [a, b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами М1 + М2 + … + Мn… т.е. имеет место неравенство │un (x)│≤ Mn. Это признак равномерной сходимости:
Даламбера
Вейерштрасса
Коши
Абеля
Лейбница
Равномерно сходящийся на отрезке [a, b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку [a, b] сходится к интегралу от суммы ряда по этому отрезку  ; α, β ; α, β  [a, b]. Это теорема о: [a, b]. Это теорема о:
почленном дифференцировании ряда
почленном произведении ряда
почленном интегрировании ряда
почленной сумме ряда
почленной разности ряда
Если члены ряда  сходится на отрезке [a, b] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных сходится на отрезке [a, b] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных  сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно: сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно: . Это теорема о: . Это теорема о:
почленном интегрировании ряда
почленном произведении ряда
почленном дифференцировании ряда
почленной сумме ряда
почленной разности ряда
Ряд вида а0 + а1х + а2х2 + … + аnxn + … =  называется: называется:
числовым рядом
функциональным рядом
степенным рядом
равномерно сходящимся рядом
рядом Фурье
Если степенной ряд а0 + а1х + а2х2 + … + аnxn + … =  сходится при х=х1, то он сходится и притом абсолютно для всех │х│>│х1│. Это теорема: сходится при х=х1, то он сходится и притом абсолютно для всех │х│>│х1│. Это теорема:
Абеля
Даламбера
Вейерштрасса
Лейбница
Коши
Если ряд  сходится, а сходится, а  │un│ расходится, то │un│ расходится, то  называется: называется:
условно сходящимся
абсолютно сходящимся
отрицательным рядом
положительным рядом
абсолютно расходящимся
Необходимое условие сходимости выполнено для ряда:





Найдите радиус сходимости степенного ряда  : :

2

0

Для исследования сходимости ряда   надо применить признак : надо применить признак :
Признак Даламбера.
Радикальный признак Коши.
Необходимый признак сходимости (достаточный признак расходимости ряда).
Признак Лейбница для знакочередующихся рядов.
Признак сравнения.
Первые три члена ряда  есть числа: есть числа:



 . .

Найдите радиус сходимости степенного ряда  : :



5.
0.
Знакопеременный ряд  называется условно сходящимся, если: называется условно сходящимся, если:
1) ряд  сходится, а ряд сходится, а ряд  расходится. расходится.
2) ряд  расходится, а ряд расходится, а ряд  сходится. сходится.
3) оба ряда  и и  сходятся. сходятся.
4) 
3.
3,2.
2.
1.
4.
Среди предложенных вариантов ответа выберите значение площади фигуры, ограниченной линиями  : :
0
1


-1
Среди предложенных вариантов ответа выберите значение площади фигуры, ограниченной линиями  : :
0

1

-1
Среди предложенных вариантов ответа выберите значение площади фигуры, ограниченной линиями |
|
 Скачать 0.78 Mb.
Скачать 0.78 Mb.