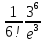|
Математика. Матан2.0. Если функция uf(x,y) имеет непрерывные смешанные производные высших порядков, то справедливо соотношение

Изменить порядок интегрирования: 


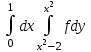


Вычислить : :
1
2
-2
-1
0
Вычислить : :
1
2
-2
-1
0
Вычислить 
10
-10
0
-23
35
Найти площадь фигуры, ограниченной данными линиями 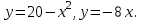
288
128
363
244
124
Пластинка  задана ограничивающими ее кривыми, задана ограничивающими ее кривыми, 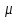 -поверхностная плотность. Найти массу пластинки. -поверхностная плотность. Найти массу пластинки.

6
12
4
9
3
Найти объем тела, заданного ограничивающими его поверхностями: 
45
24
34
25
10
Найти объем тела, заданного ограничивающими его поверхностями:

8
6
12
16
4
Найти объем тела, заданного ограничивающими его поверхностями:

16
11
26
21
6
Найти объем тела, заданного ограничивающими его поверхностями  : :
182
118
128
214
228
Найти объем тела, заданного ограничивающими его поверхностями  : :
11
16
26
21
6
Найти объем тела, заданного неравенствами  : :

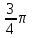

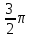
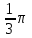
Тело  задано ограничивающими его поверхностями, задано ограничивающими его поверхностями, 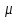 -плотность. Найти массу тела -плотность. Найти массу тела
 : :

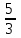



Решите уравнение y=y//+y/:
y=e-x/2(c1e +c2e +c2e ) )

y=ex(c1e +c2e +c2e ) )
y=c2ex+c1
y=c1ex+c2e-x
Решите дифференциальное уравнение у"-Зу'=0.
е3x+С.
С1+С2е3x
е3x (С1 е-3x +С2 )
С1еx+С2е3x
C1+C2e-3x.
Найти общее решение y//-5y/+6y=0:
y= (c1+c2x)e2x ;
y= c1e2x+c2e3x ;
y=c1e2x+c2e2x ;
> y= c1ex+ c2e2x ;
y=c1cosx+c2sinx+ex ;
Уравнение y’’+k*y’-b*y-sinx=0 – естьуравнение
2-гопорядка
неоднородное
3-гопорядка
однородное
n-го – порядка
. Решить уравнение первого порядка

y=
y=
y=c*x
y=
y=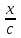
y=
y=c+x
Дифференциальное уравнение n-порядка 
называется:
однородным
линейным
уравнением Бернулли
неоднородным
уравнением Лагранжа
однородным относительно переменных
уравнением разрешенным относительно старшей производной
Если два решения однородного уравнения , то , то
решение называется на заданном [a,b] промежутке линейно-зависимыми
определитель Вронского на этом отрезке равен 0
линейно-независимыми
свободными
определитель Вронского на этом отрезке равен 1
Решитеуравнение y’=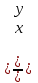 -1 -1


y=ln
y=x*ln
y=x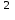 *ln *ln


Уравнение вида y’’=f(x,y’)
решается с помощью замены y’=p’;
называется дифференциальным уравнением, где явно не содержится у;
решается с помощью заменыy'=p, y’’=p’;
решается с помощью замены y’=p, y’’=p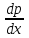 ; ;
решается с помощью замены y’=p, y’’=p ; ;
question> Уравнение вида y’+P(x)*y=Q(x)
однородное
линейное
решается с помощью подстановки y=U*V
решается с помощью подстановки y=U*x
решается с помощью подстановки y=U/x
Бернулли
Уравнение вида y’+P(x)*y=Q(x)*y , где n , где n 0, n 0, n 1,P(x), Q(x) непрерывные функции от х (или постоянные): 1,P(x), Q(x) непрерывные функции от х (или постоянные):
уравнением приводящимся к однородным;
уравнением в полных дифференциалах
называется уравнением Бернулли;
решается с помощью подстановки z = y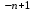
однородным уравнением;
решается с помощью подстановки y=U*V
С помощью подстановки z = y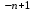 решается решается
однородное уравнение
уравнение Бернулли
Уравнение вида y’+P(x)*y=Q(x)*y , где n , где n 0, n 0, n 1 1
Уравнение вида y’+P(x)*y=Q(x)
линейное уравнение
уравнение Лагранжа
называется дифференциальным уравнением, гдене содержит у’’;
называется дифференциальным уравнением,разрешенным относительно у
Уравнение вида  называется Д У, где явно: называется Д У, где явно:
решается с помощью замены y’=p, y’’=p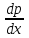 ; ;
решается с помощью замены y’=p, y’’=p ; ;
называется дифференциальным уравнением, где явно не содержитсях;
решается с помощью замены y’=p, y’’=p ; ;
называется дифференциальным уравнением, разрешенным относительно у
Вычислите: 
35

21
37
14


Вычислите: 
56

16
4
<variant>
0,25
28
В урне 18 шаров: 9 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны красный шар?

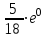
0,25


В ящике содержится 20 шаров, из них 6 красных, 4 синих и 10 белых. Найти вероятность того, что при случайном вынимании шар окажется цветным.
 . .
0,5
 . .
 . .
0,1
0,2
0,2
Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь три окрашенные грани.
0,008

0,01
0,384
0,396
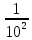
0,096
В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв О, П, Р, С, Т. Найти вероятность того , что на вынутых по одному и расположенных в одну линию можно прочесть слово «СПОРТ».
1/120
1/5!
5/17
1/100
1/5
При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов:
102

100
105
104
В денежно-вещевой лотерее на каждые 10000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразличного или вещевого, для владельца одного лотерейного билета?
0,02
1/50
0,01
0,03
0,04
0,05
1/25
В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2 деталей есть хотя бы одна стандартная.
44/45
44/45
42/45
42/45
43/45
41/45
40/45
Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком 0,7, а вторым 0,6. Найти вероятность того, что хотя бы один из стрелков попал в мишень.
0,88
22/25
0,77
0,66
0,50
У сборщика имеется 16 деталей, изготовленных заводом №1 и 4 детали завода №2. Наудачу взяты 2 детали. Найти вероятность того, что, хотя бы одна из них окажется изготовленной заводом №1




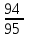
В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9; для велосипедиста – 0,8; для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму
0,86

0,85
0,84
0,80
0,83

В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина
0,9999
99,99%
0,9998
0,9989
0,999
В сосуд емкостью 10 л попала ровно одна болезнетворная бактерия. Какова вероятность зачерпнуть ее при наборе из этого сосуда стакана воды (200см3)
0,02

0,01
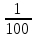
0,03
0,04
0
Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредиться, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
0,06131
0,54881
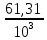
0,19537
0,00004
16Задумано двузначное число. Найти вероятность того, что задуманным числом окажется случайно названное двузначное число, цифры которого различны.

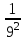
0,01

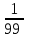
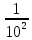
Случайная величина Х задана функцией распределения  . Найти математическое ожидание случайной величины. . Найти математическое ожидание случайной величины.


0,5



1
2.
Автоматическая телефонная станция получает в среднем 3 вызова в минуту. Вероятность того, что станция получит 6 вызовов за данную минуту, равна

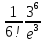

|
|
 Скачать 0.78 Mb.
Скачать 0.78 Mb.


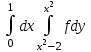


 :
: :
:

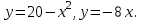
 задана ограничивающими ее кривыми,
задана ограничивающими ее кривыми, 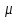 -поверхностная плотность. Найти массу пластинки.
-поверхностная плотность. Найти массу пластинки.








 :
: :
:




 :
:
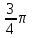

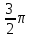
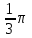
 задано ограничивающими его поверхностями,
задано ограничивающими его поверхностями, 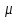 -плотность. Найти массу тела
-плотность. Найти массу тела  :
:
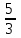



 +c2e
+c2e )
) 
 +c2e
+c2e )
) 



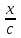


 , то
, то 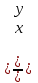 -1
-1



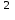 *ln
*ln


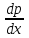 ;
; ;
; , где n
, где n 0, n
0, n 1,P(x), Q(x) непрерывные функции от х (или постоянные):
1,P(x), Q(x) непрерывные функции от х (или постоянные):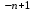
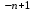 решается
решается , где n
, где n 0, n
0, n 1
1 называется Д У, где явно:
называется Д У, где явно: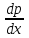 ;
; ;
; ;
;







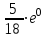


 .
.  .
.  .
. 

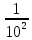








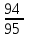



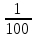
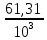

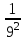

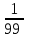
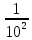
 . Найти математическое ожидание случайной величины.
. Найти математическое ожидание случайной величины.