|
Математика. Матан2.0. Если функция uf(x,y) имеет непрерывные смешанные производные высших порядков, то справедливо соотношение

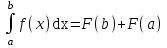 . .
Вычислить . .
cosb – cosa;
cosb;
сosa;
cosb + cosa
cosa – cosb;
Вычислить . .
8;
–8;
–6;
6;
3.
Вычислить . .
0;
–π;
x;
x + C.
π;
Геометрический смысл определенного интеграла это:
площадь круга;
площадь квадрата;
площадь прямоугольника;
площадь соответствующей пластины
площадь криволинейной трапеции;
 называется: называется:
двойным интегралом
тройным интегралом
криволинейным интегралом I рода
криволинейным интегралом II рода
поверхностным интегралом
 называется: называется:
криволинейным интегралом I рода
тройным интегралом
двойным интегралом
криволинейным интегралом II рода
поверхностным интегралом
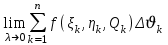 называется: называется:
двойным интегралом
криволинейным интегралом I рода
тройным интегралом
криволинейным интегралом II рода
поверхностным интегралом
Если область G-прямоугольник: a x x , ,  , то , то 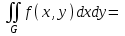

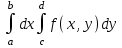
 


Если областьG ограничена снизу и сверху – непрерывными кривыми, слева и справа – прямыми, то 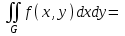




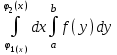
Если область G ограничена снизу и сверху- прямыми, слева и справа – непрерывными кривыми, то 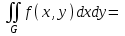


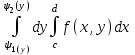

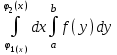
Какой интеграл с положительной подынтегральной функцией физически истолковывают как массу соответствующей пластины?
тройной интеграл
криволинейный интеграл I рода
двойной интеграл
криволинейный интеграл II рода
поверхностный интеграл
Какой интеграл с неотрицательной подынтегральной функцией геометрически истолковывают как объем соответствующего цилиндроида?
двойной интеграл
тройной интеграл
криволинейный интеграл I рода
криволинейный интеграл II рода
поверхностный интеграл
Какой интеграл с положительной подынтегральной функцией физически истолковывают как массу соответствующего тела?
тройной интеграл
двойной интеграл
криволинейный интеграл I рода
криволинейный интеграл II рода
поверхностный интеграл
Какой интеграл от единичной функции f(x,y,z) 1 численно равен объему области интегрирования? 1 численно равен объему области интегрирования?
тройной интеграл
двойной интеграл
криволинейный интеграл I рода
криволинейный интеграл II рода
поверхностный интеграл
Как называется выражение  ? ?
Градиентом скалярного поля
Дивергенцией скалярного поля
Вихрем (ротором ) векторного поля
Потоком векторного поля
Циркуляцией векторного поля
Как называется выражение  ? ?
Дивергенцией скалярного поля
Градиентом скалярного поля
Вихрем (ротором ) векторного поля
Потоком векторного поля
Циркуляцией векторного поля
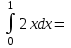
1
0
– 1
2
–2

1
0
–1
2
–2

–2
1
0
–1
2


















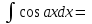













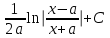

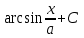
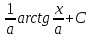

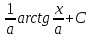
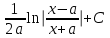

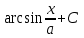


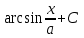
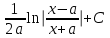

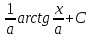



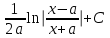
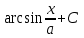
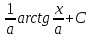


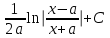

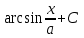
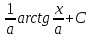

Производная функции (x,y)= в точке (x0, y0) по направлению вектора в точке (x0, y0) по направлению вектора  равна: равна:





Наибольшая скорость возрастания функции (x,y)= при переходе через точку (3, 4) равна при переходе через точку (3, 4) равна
1

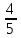
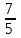
2
Градиент функции u = x2y2z2 в произвольной точке равен

72 cos + 36 cos + 24 cos
 =(72,36,24) =(72,36,24)
2xy2z2 cos + 2x2yz2 cos + 2x2y2z cos

Наибольшая скорость возрастания функции (x, y) = x2 – 2xy + 3y при переходе через точку (1, 2) равна


1

0
(x, y) = x2 – 2xy + 3y - 1. Тогда градиент  в точке (1, 2) равен в точке (1, 2) равен

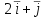



Градиент функции u = x2 – y2 + sin z в произвольной точке равен

2x – 2y + cos z
2x cos - 2y cos + cos z cos

2x – 2y - cos z
Градиент функции u = x2y2z2 в точке (1,2,3) равен
 =(72,36,24) =(72,36,24)

2xy2z2 cos + 2x2yz2 cos + 2x2y2z cos
72 cos + 36 cos + 24 cos
2xy2z2 + 2x2yz2 + 2x2y2z
Производная функции (x, y) = ln (x + y) в точке (1, 2) по направлению биссектрисы первого координатного угла  равна равна



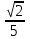

Производная функции f(x, y) = x2 + y2 – 4yz в точке (0, 1, 2) по направлению к точке (2, 3, 3) равна





Наибольшая скорость изменения функции u(x, y, z) в точке M(x, y, z) равна

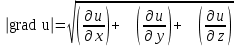



Наибольшая скорость возрастания функции (x, y) =  при переходе через точку (-1, 1, -1) равна при переходе через точку (-1, 1, -1) равна


1

0
Градиент функции (x, y) =  в точке (-1, 1, -1) равен в точке (-1, 1, -1) равен
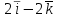
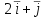



Направляющие косинусы вектора  = (2, 2, 1) равны = (2, 2, 1) равны





Формула это это
формула вычисления двойного интеграла в полярных координатах
формула вычисления момента инерции плоской фигуры
формула вычисления тройного интеграла в декартовых координатах
формула вычисления тройного интеграла в цилиндрических координатах
формула вычисления тройного интеграла в сферических координатах
Формула 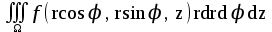 это это
формула вычисления тройного интеграла в цилиндрических координатах
формула вычисления двойного интеграла в полярных координатах
формула вычисления момента инерции плоской фигуры
формула вычисления тройного интеграла в декартовых координатах
формула вычисления тройного интеграла в сферических координатах
Формула  это это
формула вычисления тройного интеграла в сферических координатах
формула вычисления двойного интеграла в полярных координатах
формула вычисления момента инерции плоской фигуры
формула вычисления тройного интеграла в декартовых координатах
формула вычисления тройного интеграла в цилиндрических координатах
Найти интеграл 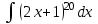 : :
 (2х+1)21 + С. (2х+1)21 + С.
 (2х+1)21 + С. (2х+1)21 + С.
(2х+1)21 + С.
 (2х+1)20 + С (2х+1)20 + С
(2х+1)20 + С.
Найтиинтеграл : :
-  . .
 . .
 . .
 . .
 . .
Найтиинтеграл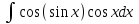 : :
sin(sin x) + C.
sin(cos x) + C.
-sin(sin x) + C.
-sin(cos x) + C.
cos(sinx)+C.
Найтиинтеграл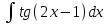 : :
–  . .
 . .
- . .
  . .
  . .
Найтиинтеграл : :
 . .
- . .
 . .
 . .
 . .
Вычислить : :
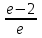 . .
 . .
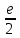 . .
e – 1.
e – 2.
Найтиинтеграл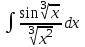 : :
2cos +C. +C.
-cos +C. +C.
1/3 cos +C. +C.
1/3 sin +C. +C.
-3 cos +C. +C.
Найти площадь фигуры, ограниченной линиями х = 0, х = , у = 0, у = sinx:
2.
1 .
–1.
0.
–2.
Найти площадь фигуры, ограниченной линиями х = 2, у = 0, у = х3:
4.
2.
3.
1.
0.
Вычислить : :
10,5.
21.
0,5.
20.
0,1.
Найтиинтеграл : :
 . .
 . .
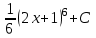 . .
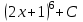 . .
|
|
 Скачать 0.78 Mb.
Скачать 0.78 Mb.
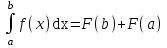 .
. .
. .
. .
. называется:
называется: называется:
называется: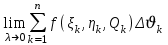 называется:
называется: x
x ,
,  , то
, то 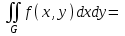

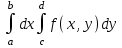




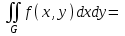




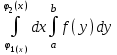
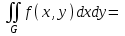


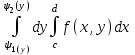

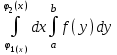
 1 численно равен объему области интегрирования?
1 численно равен объему области интегрирования? ?
? ?
?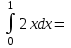




















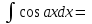













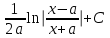

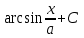
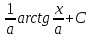

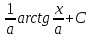
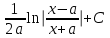

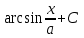


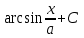
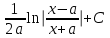

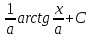



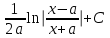
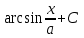
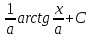


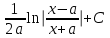

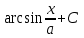
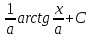

 в точке (x0, y0) по направлению вектора
в точке (x0, y0) по направлению вектора  равна:
равна:




 при переходе через точку (3, 4) равна
при переходе через точку (3, 4) равна
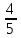
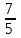

 =(72,36,24)
=(72,36,24)



 в точке (1, 2) равен
в точке (1, 2) равен
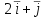





 =(72,36,24)
=(72,36,24) 
 равна
равна


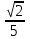







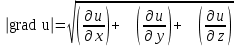



 при переходе через точку (-1, 1, -1) равна
при переходе через точку (-1, 1, -1) равна


 в точке (-1, 1, -1) равен
в точке (-1, 1, -1) равен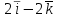
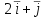



 = (2, 2, 1) равны
= (2, 2, 1) равны




 это
это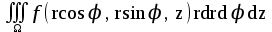 это
это это
это 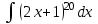 :
: (2х+1)21 + С.
(2х+1)21 + С. (2х+1)21 + С.
(2х+1)21 + С. (2х+1)20 + С
(2х+1)20 + С :
:
 .
. .
. .
. .
. .
.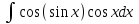 :
: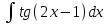 :
:
 .
. .
. .
.
 .
.
 .
. :
: .
. .
. .
. .
. .
. :
: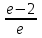 .
. .
.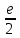 .
.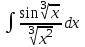 :
: +C.
+C.  +C.
+C. +C.
+C. +C.
+C. +C.
+C. :
: :
: .
. .
.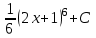 .
.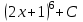 .
.