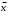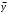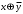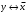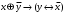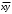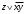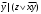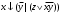Дискретка. Факультет автф преподаватель
 Скачать 119.86 Kb. Скачать 119.86 Kb.
|
|
Новосибирский государственный технический университет Типовой расчет по дискретной математике Факультет: АВТФ Преподаватель: Группа: АВТ-415 Чиркунов Ю.А. Студент: Слинько И. А. Вариант 23
Новосибирск 2015г. Задание 1. Докажите тождества, используя только определения операций над множествами 1) 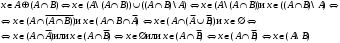 2) 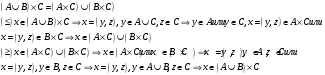 Задание 2. Докажите утверждение. 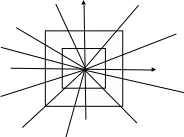 Множество точек двух квадратов эквивалентны Множество точек двух квадратов эквивалентныЗадание 3. Докажите методом математической индукции 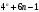 кратно 9 при всех натуральных n>0. (*) кратно 9 при всех натуральных n>0. (*)Установим басиз индукции, то есть проверим справедливость соотношения для наименьшего n. 41+6*1-1==4+6-1=9 9  9 9Басиз установлен. Установим шаг индукции – возможность индуктивного перехода 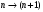 Пусть верно (*), используя (*) пусть верно для n+1 4n+1+6(n+1)-1=4*4n+6n+5=4(4n+6n-1-6n+1)+6n+5=4(4n+6n-1)-24n+4+6n+5=4(4n+6n-1)-18n+9 4(4n+6n-1)  9 из (*) 9 из (*)-18n 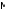 9 99 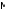 9 9Шаг индукции установлен. В силу метода математической индукции формула доказана. Задание 4. Пусть А={a,b,c}, B={1,2,3,4}, 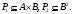 Изобразите отношения P1 и P2 графически. Найдите Изобразите отношения P1 и P2 графически. Найдите 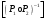 . Проверьте с помощью матрицы [P2] является ли отношение P2 рефлексивным, симметричным, антисимметричным, транзитивным? . Проверьте с помощью матрицы [P2] является ли отношение P2 рефлексивным, симметричным, антисимметричным, транзитивным?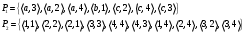 P1 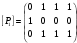 P2 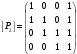 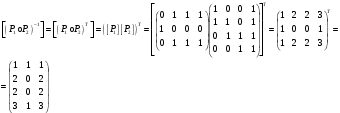 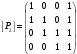 - по диагонали нет нулей - по диагонали нет нулей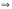 P2 рефлексивно P2 рефлексивно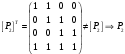 несимметрично несимметрично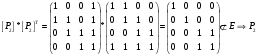 неантисимметрично неантисимметрично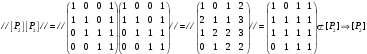 нетранзитивно нетранзитивноЗадание 5. Найдите область определения, область значений отношения P. Является ли отношение P рефлексивным, симметричным, антисимметричным, транзитивным? 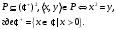 Область определения: 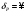 Область значений: 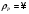 P нерефлексивно: 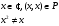 P несимметрично: 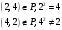 P неантисимметрично: 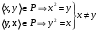 P нетранзитивно: 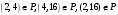 Задание 6. Является ли алгеброй следующий набор 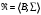 ? ?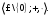 1) 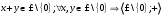 - алгебраическая система - алгебраическая система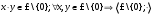 - алгебраическая система - алгебраическая система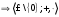 - алгебраическая система - алгебраическая система2) “+”: 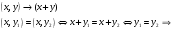 ”+” – функция ”+” – функция“  ”: ”: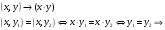 ” ” ” – функция ” – функция 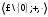 - алгебра. - алгебра.Задание 9. Даны графы G1 и G2. Найдите 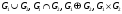 . Для графа . Для графа 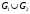 найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1. найдите матрицы смежности, инцидентности, сильных компонент, маршрутов длины 2 и все маршруты длины 2, исходящие из вершины 1.Рассмотрим 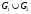 : :Матрица смежности 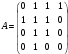 Дуги 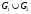 : a1=(1,2), a2=(1,3), a3=(1,4), a4=(2,1), a5=(2,2), a6=(2,3), a7=(3,2), a8=(3,3),a9=(4,2) : a1=(1,2), a2=(1,3), a3=(1,4), a4=(2,1), a5=(2,2), a6=(2,3), a7=(3,2), a8=(3,3),a9=(4,2)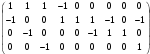 - матрица инцидентности - матрица инцидентностиB=E+A+A2+A3= 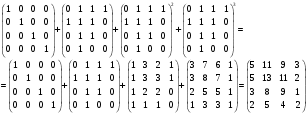 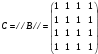  - матрица сильных компонент - матрица сильных компонентА2=  - матрица маршрутов длины 2. - матрица маршрутов длины 2.Маршрут длины 2, исходящие из вершины 1: (1;2;1), (1;2;2), (1;2;3), (1;3;2), (1;3;3), (1;4;2) Задание 11. Составьте таблицы истинности формул. 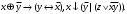 1)
2)
|