экономическая статистика контрольная. Финансовый университет при Правительстве Российской Федерации
 Скачать 187.17 Kb.
|
|
Вывод. Анализ интервального ряда распределения изучаемой совокупности предприятий показывает, что распределение предприятий по среднегодовой заработной плате не является равномерным: преобладают предприятия со среднегодовой заработной платой от 230 тыс.руб. До 260 тыс.руб. (это 12 предприятий, доля которых составляет 40%); самые малочисленные группы предприятий имеют 170-200 тыс.руб. 2. Нахождение моды и медианы полученного интервального ряда распределения графическим методом и путём расчётов. Для определения моды графическим методом строим по данным табл. 4 (графы 2 и 3) гистограмму распределения фирм по изучаемому признаку.    Рис. 1 Определение частоты графическим методом Расчет конкретного значения модыдля интервального ряда распределения производится по формуле:  где хМo – нижняя граница модального интервала, h –величина модального интервала, fMo – частота модального интервала, fMo-1 – частота интервала, предшествующего модальному, fMo+1 – частота интервала, следующего за модальным. Согласно таблице 4 модальным интервалом построенного ряда является интервал 230-260 тыс. руб., т.к. его частота максимальна (f3 = 12). Расчет моды:  Вывод. Для рассматриваемой совокупности предприятий наиболее распространенная среднегодовая заработная плата характеризуется средней величиной 246 тыс. руб. Для определения медианы графическим методом строим по данным табл. 5 (графы 2 и 5) кумуляту распределения фирм по изучаемому признаку.   Рис. 2. Определение медианы графическим методом Расчет конкретного значения медианы для интервального ряда распределения производится по формуле 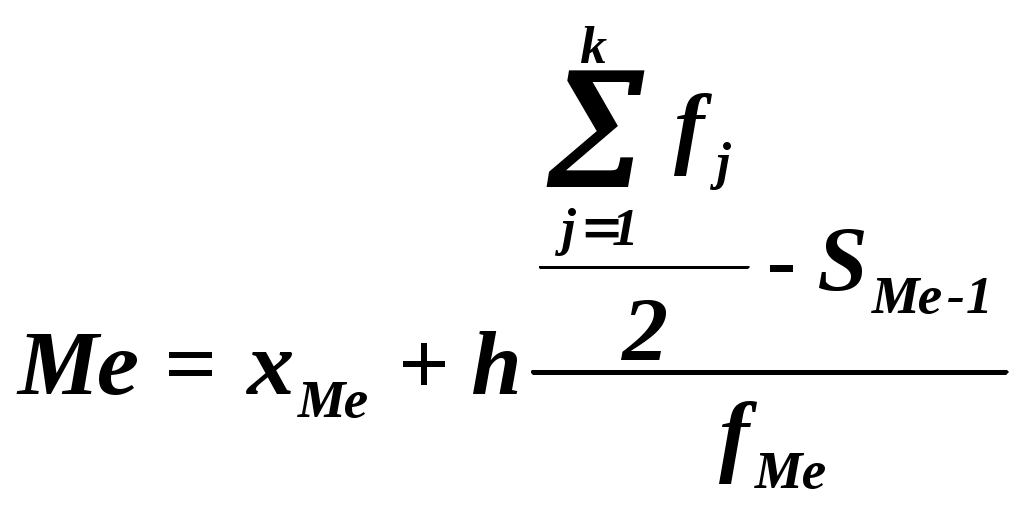 где хМе– нижняя граница медианного интервала, h – величина медианного интервала,  – сумма всех частот,fМе – частота медианного интервала, SMе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному. Определяем медианный интервал, используя графу 5 табл. 5. Медианным интервалом является интервал 230-260 тыс.руб., т.к. именно в этом интервале накопленная частота Sj=21 впервые превышает полусумму всех частот (  = ).Расчет значения медианы по формуле (4):  Вывод. В рассматриваемой совокупности предприятий половина предприятий имеют среднегодовую заработную плату не более 245 тыс. руб., а другая половина – не менее 245 тыс. Руб. 3. Расчет характеристик ряда распределения Для расчета характеристик ряда распределения  , σ, σ2, Vσ на основе табл. 5 строится вспомогательная таблица 6 ( – середина j-го интервала).Таблица 6 Расчетная таблица для нахождения характеристик ряда распределения
Рассчитаем среднюю арифметическую взвешенную: 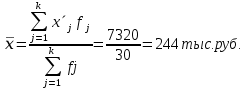 Рассчитаем среднее квадратическое отклонение: 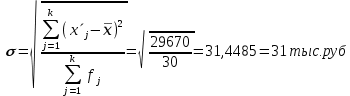 Рассчитаем дисперсию:  Рассчитаем коэффициент вариации:  Вывод. Анализ полученных значений показателей и σ говорит о том, что средняя величина среднегодовой заработной платы составляет 244 тыс. руб., отклонение от этой величины в ту или иную сторону составляет в среднем 31 тыс.руб. (или 12,9%), наиболее характерная среднегодовая заработная плата находится в пределах от 213 тыс.руб до 275 тыс.руб. (диапазон  ).Значение Vσ = 12,9% не превышает 33%, следовательно, вариация среднегодовой заработной платы в исследуемой совокупности предприятий незначительна и совокупность по данному признаку однородна. Расхождение между значениями , Мо и Ме незначительно ( =244 тыс.руб., Мо=246тыс.руб., Ме=245 тыс.руб.), что подтверждает вывод об однородности совокупности предприятий. Таким образом, найденное среднее значение среднегодовой заработной платы (244 тыс.руб.) является типичной, надежной характеристикой исследуемой совокупности предприятий. 4. Вычисление средней арифметической по исходным данным о среднегодовой заработной плате предприятий Для расчета применяется формула средней арифметической простой: 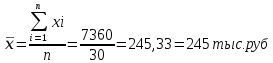 Причина расхождения средних величин, рассчитанных по исходным данным (245 тыс.руб.) и по интервальному ряду распределения (244 тыс.руб.), заключается в том, что в первом случае средняя определяется по фактическим значениям исследуемого признака для всех 30-ти предприятий, а во втором случае в качестве значений признака берутся середины интервалов и, следовательно, значение средней будет менее точным ( за исключением случая равномерного распределения значений признака внутри каждой группы.)Задание 2 По исходным данным (табл. 1) с использованием результатов выполнения Задания 1 необходимо выполнить следующее: Установить наличие и характер корреляционной связи между признаками Среднегодовая заработная платаиФонд заработной платы, образовав по каждому признаку пять групп с равными интервалами, используя методы: а) аналитической группировки; б) корреляционной таблицы. 2. Измерить тесноту корреляционной связи, используя коэффициент детерминации и эмпирическое корреляционное отношение. Сделать выводы по результатам выполнения задания 2. Выполнение задания 2 Целью выполнения данного задания является выявление наличия корреляционной связи между факторным и результативным признаками, а также установление направления связи и оценка ее тесноты. По условию Задания 2 факторным является признак Среднегодовая заработная плата, результативным – признак Фонд заработной платы. 1. Установление наличия и характера корреляционной связи между признаками Среднегодовая заработная плата иФонд заработной платыметодами аналитической группировки и корреляционных таблиц 1а. Применение метода аналитической группировки Аналитическая группировка строится по факторному признаку Х и для каждой j-ой группы ряда определяется среднегрупповое значение  результативного признака Y. Если с ростом значений фактора Х от группы к группе средние значения систематически возрастают (или убывают), между признаками X и Y имеет место корреляционная связь.Используя разработочную таблицу 3, строим аналитическую группировку, характеризующую зависимость между факторным признаком Х – Среднегодовая заработная платаи результативным признаком Y – Фонд заработной платы. Групповые средние значения  получаем из таблицы 3 (графа 4), основываясь на итоговых строках «Всего». Построенную аналитическую группировку представляет табл. 7:Таблица 7 Зависимость среднегодовой заработной платы от фонда заработной платы
Вывод. Анализ данных табл. 7 показывает, что с увеличением среднегодовой заработной платы от группы к группе систематически возрастает и средний фонд заработной платы по каждой группе, что свидетельствует о наличии прямой корреляционной связи между исследуемыми признаками. 1б. Применение метода корреляционных таблиц Корреляционная таблица строится как комбинация двух рядов распределения по факторному признаку Х и результативному признаку Y. На пересечении j-ой строки и k-ой графы таблицы указывается число единиц совокупности, входящих в j-ый интервал по признаку X и в k-ый интервал по признаку Y. Концентрация частот около диагонали построенной таблицы свидетельствует о наличии корреляционной связи между признаками - прямой или обратной. Связь прямая, если частоты располагаются по диагонали, идущей от левого верхнего угла к правому нижнему, обратная - по диагонали от правого верхнего угла к левому нижнему. Для построения корреляционной таблицы необходимо знать величины и границы интервалов по двум признакам X и Y. Для факторного признака Х – Среднегодовая заработная плата эти величиныизвестны из табл. 4. Определяем величину интервала для результативного признака Y – Фонд заработной платы при k= 5, уmax= 5,160 млн.руб., уmin= 1,760 млн.руб.:  Границы интервалов ряда распределения результативного признака Y имеют вид: Таблица 8
Подсчитывая для каждой группы число входящих в нее предприятий с использованием принципа полуоткрытого интервала [ ), получаем интервальный ряд распределения результативного признака (табл. 9). Таблица 9 Интервальный ряд распределения предприятий по фонду заработной платы
Используя группировки по факторному и результативному признакам, строим корреляционную таблицу (табл. 10). Таблица 10 Корреляционная таблица зависимости фонда заработной платы от среднегодовой заработной платы
Вывод. Анализ данных табл. 10 показывает, что распределение частот групп произошло вдоль диагонали, идущей из левого верхнего угла в правый нижний угол таблицы. Это свидетельствует о наличии прямой корреляционной связи между среднегодовой заработной платой и фондом заработной платы. 2. Измерение тесноты корреляционной связи с использованием коэффициента детерминации  и эмпирического корреляционного отношения  Коэффициент детерминации характеризует силу влияния факторного (группировочного) признака Х на результативный признак Y и рассчитывается как доля межгрупповой дисперсии  признака Y в его общей дисперсии : , где  – общая дисперсия 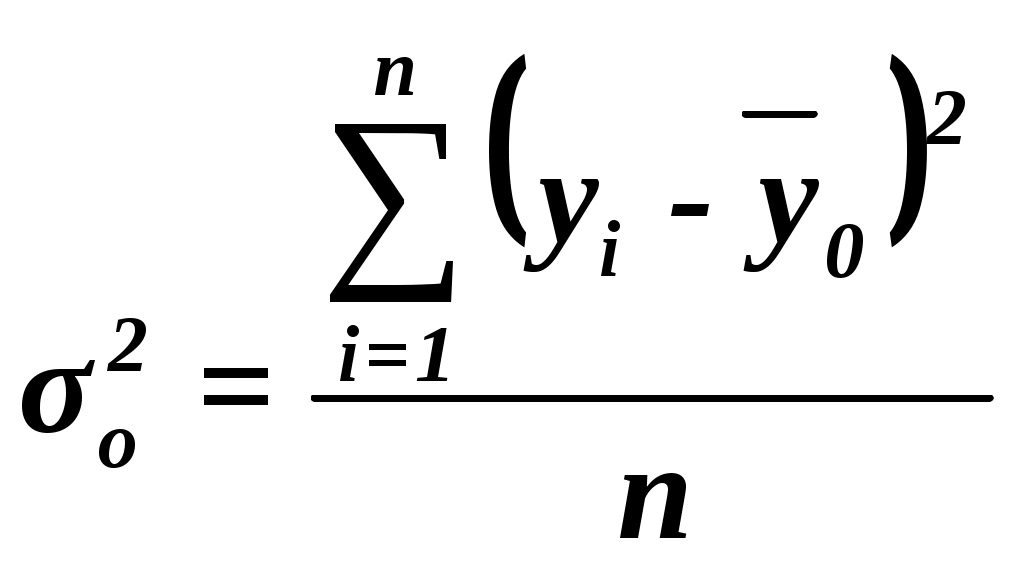признака Y, – межгрупповая (факторная) дисперсия признака Y.Общая дисперсия характеризует вариацию результативного признака, сложившуюся под влиянием всех действующих на Y факторов (систематических и случайных). Этот показатель вычисляется по формуле (10) где yi – индивидуальные значения результативного признака;  – общая средняя значений результативного признака;n – число единиц совокупности. Межгрупповая дисперсия измеряет систематическую вариацию результативного признака, обусловленную влиянием признака-фактора Х (по которому произведена группировка). Воздействие фактора Х на результативный признак Y проявляется в отклонении групповых средних от общей средней  . Показатель вычисляется по формуле , где –групповые средние, – общая средняя, –число единиц в j-ой группе,k – число групп. Для расчета показателей и необходимо знать величину общей средней , которая вычисляется как средняя арифметическая простая по всем единицам совокупности:  (11) Значения числителя и знаменателя формулы имеются в табл. 7 (графы 3 и 4 итоговой строки). Используя эти данные, получаем общую среднюю : Для расчета общей дисперсии применяется вспомогательная таблица 11. Таблица 11 Вспомогательная таблица для расчета общей дисперсии
Рассчитаем общую дисперсию:  Для расчета межгрупповой дисперсии строится вспомогательная таблица 12. При этом используются групповые средние значения из табл. 7 (графа 5). | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
