Физика ядерной медицины

• Название: Физика ядерной медицины
• Анкор: Part 1.docx
• Дата: 28.01.2017
• Размер: 9.62 Mb.
• Имя файла: Part 1.docx
• Тип: Документы; #616
• страница: 36 из 40

Глава 8. Производство радионуклидов

В настоящее время известно около 1850 нуклидов, 280 из которых стабильны. В земной коре и океанских и морских водах находится ряд естественных долгоживущие радионуклидов (р/н), образующих цепочки последовательного радиоактивного распада. Этот ряд включает ²³⁵U, ²³⁸U, ²³²Th. Кроме того на Земле имеется 16 других долго живущих естественных р/н, включая ⁴⁰K, ⁵⁰V, ⁸⁷Rb,¹¹³Cd и ¹¹⁵In. Дополнительно некоторое количество короткоживущих р/н образуется из естественных источников и космическими лучами.

Большинство р/н создается искусственно путем превращения стабильных нуклидов в нестабильные нуклиды с помощью бомбардирования их нейтронами. протонами, дейтеронами, α-частицами, γ-излучением и другими ядерными частицами. Источником этих частиц могут быть р/н, ядерные реакторы или различного типа ускорители. Большое разнообразие искусственно созданных р/н способствовало прогрессу во многих приложениях физики, биологии, и конечно, медицине. Производство р/н в краткой общей форме было рассмотрено в разделе 5 главы1, в данной главе этот материал дополнен обсуждением специфических вопросов производства и использования р/н в ЯМ.

1. Уравнения производства радионуклидов

Скорость распада радиоактивного образца, как известно (см. главу 1), пропорциональна числу имеющихся в данный момент атомов, 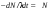. Интегрирование этого уравнения приводит к также хорошо известному экспоненциальному закону радиоактивного распада 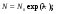где λ – постоянная распада и N₀ – первоначальное число атомов (на момент времени t = 0).

Из предыдущих рассмотрений (см. глава 1) было видно, что производство данного р/н пропорционально числу атомов мишени N_t, плотности потока падающих частиц φ (в частности, нейтронов), и поперечному сечению реакции σ. Образовавшийся продукт сам испытывает радиоактивный распад. Таким образом, результирующая скорость изменения числа радиоактивных ядер продукта N_p в течение облучения равна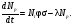

(8.1)

Так как N_p обычно в ЯМ настолько велико, что остается постоянным в течение облучения, то решение уравнения (8.1) есть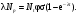

(8.2)

Активность продукта A_p к концу облучения равна λN, откуда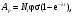

(8.3)

где N_t= (m/M)N_AF; m – масса образца в граммах; N_A – число Авогадро; M– атомная масса в г/моль; F – относительное содержание изотопа; φ – плотность потока падающих частиц в 1/(см²·с); σ – поперечное сечение в см²; λ – постоянная распада продукта в с^-1; t – время облучения.

Отметим, что в случае большого времени облучения t_irrad << T_1/2 продукта, фактор (1-exp(-λt)) стремится к 1. Это означает, что скорость образования и скорость распада продукта сравниваются, или, как говорят, реакция достигла насыщения. На практике облучение в течение времени больше, чем период полураспада продукта считается относительно неэффективным.

В полученный результат (уравнение (8.3) следует внести корректировку, когда образец достаточно велик или время облучения очень продолжительно. Для массивной мишени с большим поперечным сечением взаимодействия будет наблюдаться заметное поглощение нейтронов в наружных слоях мишени, что уменьшит эффективную плотность потока нейтронов. Этот эффект трудно рассчитать простыми методами (необходимо применить строгие методы теории переноса) и он обычно измеряется.

Уравнения производства может иметь одну из двух форм в зависимости от того, облучается ли мишень изотропно в ядерном реакторе или мононаправленным пучком ускорителя. В последнем случае поперечные размеры мишени обычно шире диаметра пучка, и мишень облучается в конкретном направлении. Здесь важно знание доли мишени, находящейся под облучением. Тогда наработанная активность для тонкой мишени равна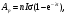

(8.4)

где 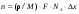в атом/см²; ρ – плотность мишени в г/см³; Δx – толщина мишени в см; I – ток пучка (число бомбардирующих частиц в единицу времени).

В случае толстой мишени необходимо учитывать пробег бомбардирующих частиц в мишени и изменение поперечного сечения взаимодействия при уменьшении энергии частиц на длине пробега при линейных потерях энергии частиц (в частности, протонов) в мишени (dE/dx). Таким образом, активность продукта будет равна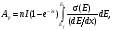

(8.5)

где E_i и E_f –начальная и финальная энергия частицы, соответственно.

На практике интеграл в формуле (8.5) разбивают на тонкие слои, в пределах которых σ(E) можно считать постоянным. Для сложного вещества пробег частицы можно аппроксимировать согласно аддитивному правилу Брэгга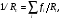

(8.6)

где R_с – пробег в сложном веществе; R_i– пробег в i-элементе; f_i – весовая доля i-элемента в сложном веществе.