На протяжении истории ЯМ различные технологии ОФЭКТ использовались. Эти технологии включают ограниченно-угловую томографию (например, фокально-плоскостная камера Ангера, семипинхольный коллиматор, коллиматор с наклонными каналами) и трансаксиальную (поперечную) томографию. В настоящее время доминирующее положение занимает трансаксиальная томография, которую разделяют на несколько классов, исходя из применяемого алгоритма реконструкции изображений (обратное проектирование, фильтрованное обратное проектирование и итерационные алгоритмы).
Трансаксиальная томография представляет измерение изображений объекта перпендикулярно к главной оси под разными углами в диапазоне от 0 до 180 или до 360 градусов. На базе такого набора изображений становится возможной аналитическая реконструкция данных для получения поперечных срезов (англ. slice) заданной толщины перпендикулярно продольной оси пациента (рис. 7.7). Для упрощения изложения введем несколько понятий.
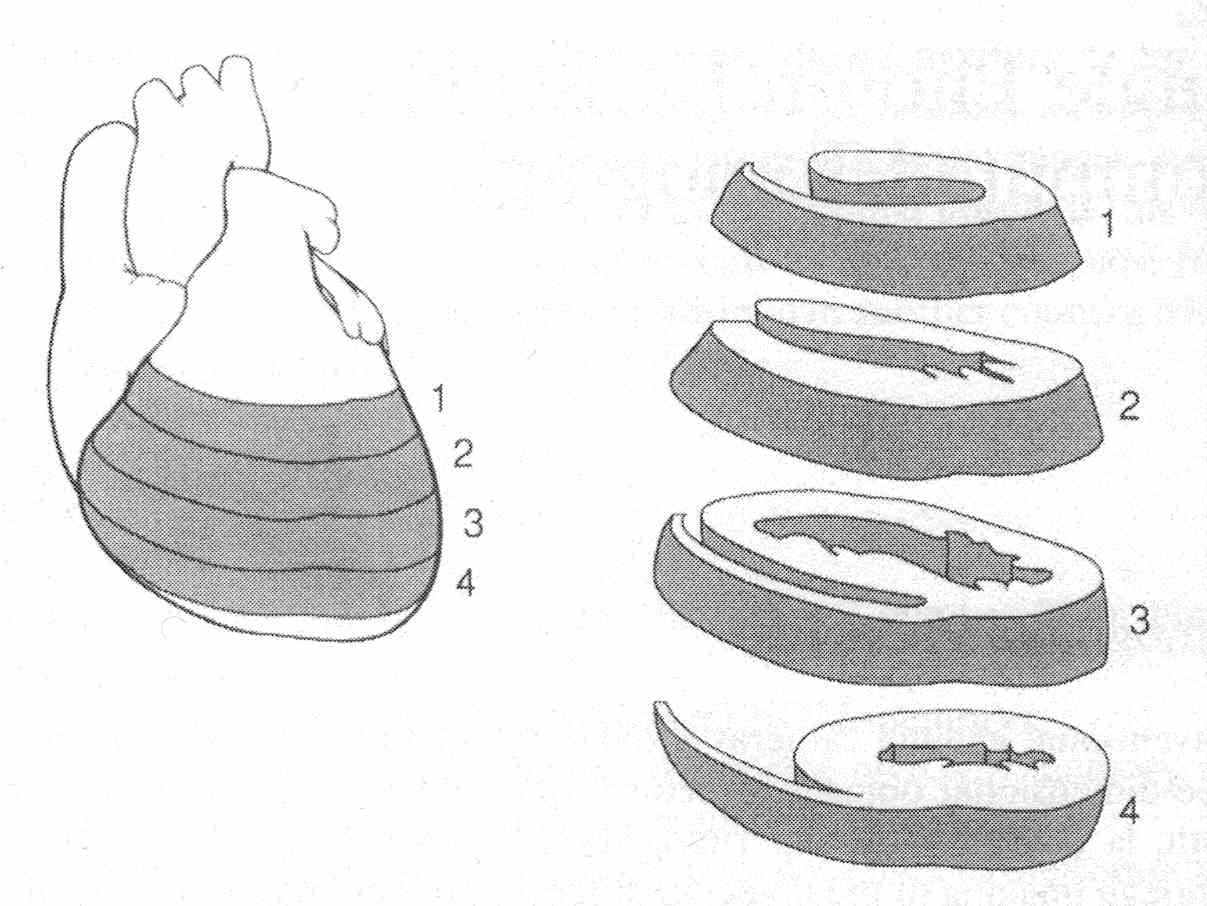
Рис. 7.7. Четыре среза сердца вдоль короткой оси [1]
Каждый угол, при котором производится измерение, будем называть полем зрения или ракурсом. Если, например, измерение изображений проводится для 64 углов в диапазоне от 0 до 360о, то набор данных состоит из 64 ракурсов. Для каждого ракурса выполняется измерение изображения в полном поле зрения. Каждое изображение в этом наборе является проекцией всех структур, находящихся в поле зрения, на плоскую поверхность детектора камеры в конкретном направлении. Так как данные собираются в цифровом виде, каждое поле зрения является дискретным описанием изображения и состоит из двумерного массива (матрицы) пикселей.
Данные в каждой строчке матрицы представляют срез толщиной как размер пикселя. Таким образом, если для накопления данных с квадратного поля зрения со стороной 38 см применяется матрица 64 × 64, то номинальный размер пикселя 6 мм и каждая строчка в матрице в идеале представляет проекцию 6-мм среза пациента (рис. 7.8). Идеальная ситуация подразумевает здесь идеальный детектор с отличным разрешением и отсутствие рассеяния. В действительности данные в строчке будут включать вклад от фотонов, испущенных с площади, превосходящей размер пикселя.
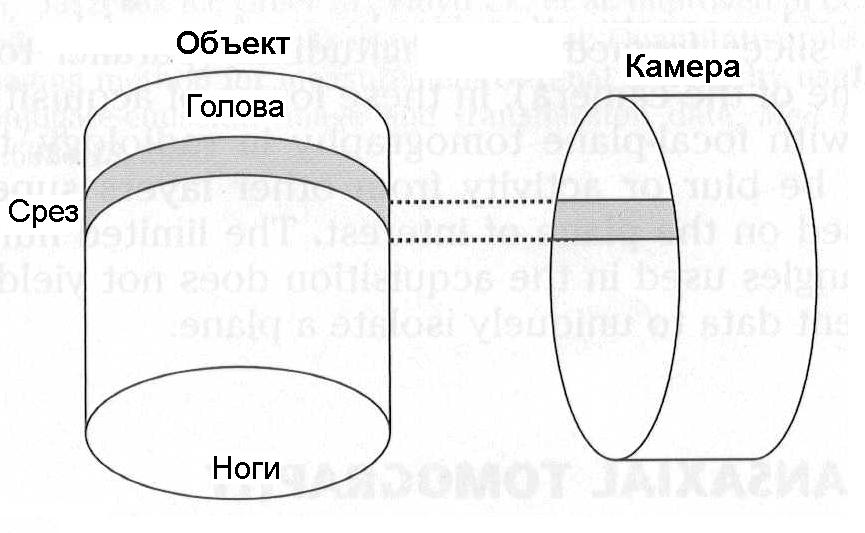
Рис. 7.8. Схематическая иллюстрация набора данных для конкретного среза в трансаксиальной томографии [1]
В заключение рассмотрим концепцию выборки. Каждая строчка в описанном выше примере состоит из 64 выборочных значений (проб) поперек изображаемой части объекта. Отдельный пиксель внутри строчки представляет сумму лучей, т.е. сумма излучений от активностей вдоль линии перпендикулярной к камере (ослабленной структурами, находящимися на пути лучей). Количество значений в выборке связано с максимальным разрешением, возможным в окончательном реконструированном изображении. С увеличением количества проб улучшается пространственное разрешение финального результата.
Суммируя обсуждение, повторно отметим, что каждый угол, в направлении которого проводится измерение томографического изображения, является полем зрения или ракурсом. Каждое поле зрения состоит из профилей или проекций данных от такого же количества срезов, как количество строчек в матрице, и каждый срез имеет такое же число выборочных значений как число пикселей в строчке.
Реконструкция изображений
Данные, набранные в виде двумерных проекций, дают плоское изображение объекта для каждого ракурса. Для получения информации по глубине объекта, томографические изображения реконструируются, используя эти проекции. Наибольшее распространение в настоящее время получили два метода реконструкции: метод обратного проецирования (МОП) и итерационный метод. Первый из них более популярен, однако второй в последнее время привлекает большее внимание. Рассмотрим их подробнее.
3.1 Простое обратное проецирование
Принцип метода простого обратного проецирования для реконструкции изображений иллюстрируется на рис. 7.9. На рис. 7.9,а показаны три положения детекторной головки гамма-камеры вокруг исследуемого объекта, при которых проводится двумерный набор данных, спроектированных под данным ракурсом. Объект содержит два источника излучения. Число отсчетов в каждом пикселе для данной проекции представляет сумму всех отсчетов вдоль пути по прямой линии через глубину объекта. Реконструкция проводится присваиванием всем пикселям вдоль линии набора (перпендикулярно лицевой стороне камеры) в реконструированной матрице числа отсчетов в каждом пикселе для данной проекции в матрице набора (рис. 7.9,б). Это называется простым обратным проектированием (МПОП). В результате обратного проецирования множества проекций создается финальное изображение, показанное на рис. 7.9,в.
Обратное проецирование может быть лучше понято в терминах набора данных в матрицы. Пусть данные накапливаются в матрице сбора данных 4 × 4 (рис. 7.10,а). В этой матрице каждая строчка представляет срез, проекцию, или профиль определенной толщины и обратно проектируется индивидуально. Отдельный ряд состоит из четырех пикселей. Например, первая строчка имеет пиксели A1, B1, C1 и D1. Число отсчетов в каждом пикселе является суммой всех отсчетов вдоль глубины в просматриваемом направлении. В МОП создается новая реконструкционная матрица такого же размера (4 × 4) путем добавления числа отсчетов в пикселе A1 матрицы сбора в каждый пиксель первого столбца матрицы реконструкции (рис. 7.10,б). Такая же операция производится с числом отсчетов в пикселях B1, C1 и D1 , только они добавляются в каждый пиксель второго, третьего и четвертого столбцов матрицы реконструкции, соответственно.
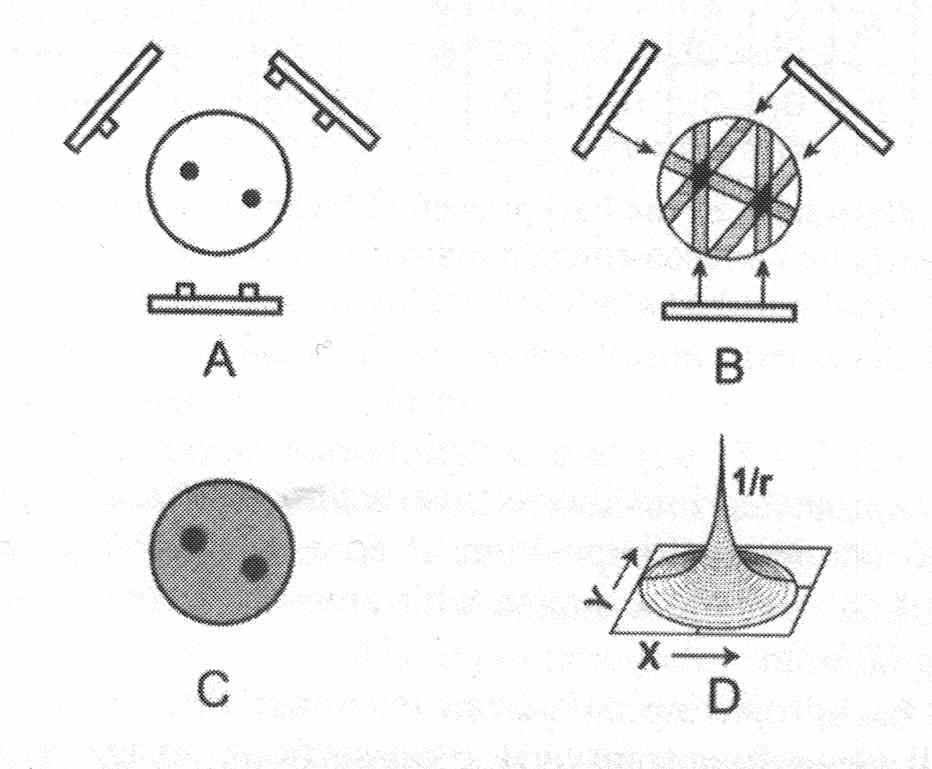
Рис. 7.9. Иллюстрация основного принципа реконструкции изображения методом обратного проектирования: А – излучение, выходящее из объекта с двумя "горячими пятнами" (сплошные сферы), измеряется в трех проекциях, расположенных под углом 120о относительно друг друга; B – собранные данные используются для реконструкции; C – Из множества проекций создается реконструированное изображение объекта в данном сечении; D – эффект размытия, описываемый функцией 1/r, где r расстояние от центральной точки [8].
Далее предположим, что набор данных проводится с бокового направления (90о) и данные накапливаются опять в 4 × 4 матрице набора. Первая строка этой матрицы, состоящая из пикселей A2, B2, C2 и D2, показана на рис. 7.10,в. Число отсчетов в пикселе A2 добавляется в каждый пиксель первого столбца той же матрицы реконструкции, в пикселе B2 в каждый пиксель второго столбца и т.д. Если будут проведены измерения и под другими углами, то первую строку данных, накопленных с каждого направления в матрице сбора, следует таким же образом проецировать обратно в матрицу реконструкции. Этот способ обратного проецирования приводит в результате к суперпозиции данных с каждой проекции, тем самым формируя окончательное поперечное изображение с участками увеличенной или уменьшенной активности (рис. 7.10,в).
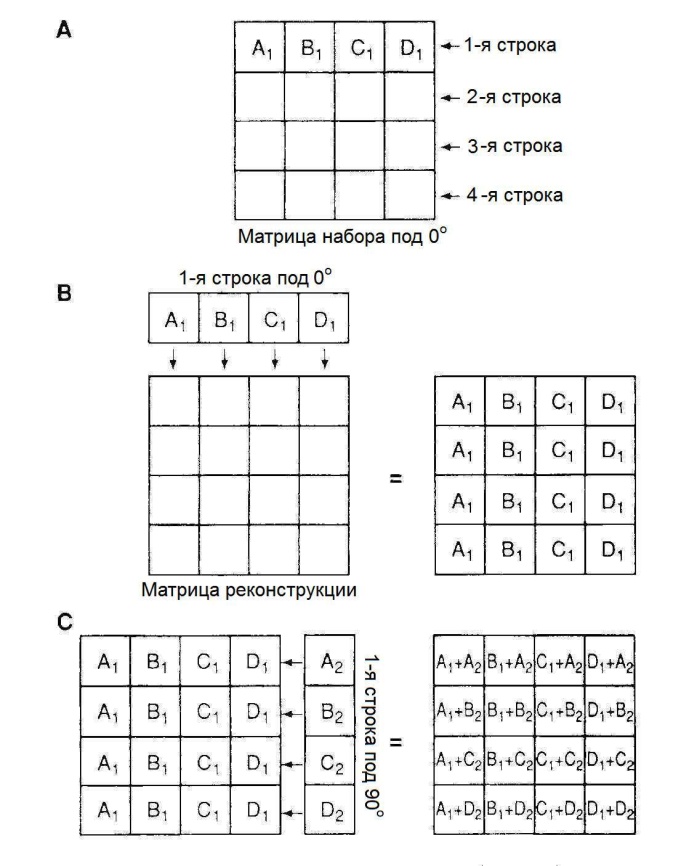
Рис. 7.10. Иллюстрация метода обратного проецирования, используя данные из матрицы набора в матрице реконструкции [8]
Подобным же образом проводится обратное проецирование данных, которые накапливаются в трех других строчках матрицы набора. Они соответствуют измерениям, выполненных от других срезов объекта. В результате создаются поперечные изображения объекта в четырех поперечных срезах. Если для накопления и реконструкции применяются матрицы 64 × 64, то генерация поперечных изображений проводится в 64 срезах. Из этих поперечных изображений с помощью соответствующей выборки и упорядочивания пикселей вдоль вертикальной и горизонтальной осей можно сформировать сагиттальное и коронарное изображения. Для уменьшения статистических флуктуаций на практике часто применяется объединение (свертывание) отсчетов из нескольких срезов в один.
3.2. Обратное проецирование с фильтрацией
МПОП имеет проблему "звездообразных" артефактов (рис. 7.10.в), вызываемых проникновением излучения со смежных областей с увеличенной активностью (англ. "shining through"). В результате происходит размытие изображения объекта. Так как эффект размытия уменьшается с увеличением расстояния r от объекта интереса, то его допустимо приближенно описать функцией 1/r (рис. 7.10,г). Возникновение "звездообразных" артефактов можно рассматривать как "переливание" определенного количества отсчетов из пикселя интереса в соседние пиксели. Эффект размытия возможно минимизировать, применяя фильтрацию к данным в матрице набора, и уже фильтрованные проекции включать в процесс обратного проецирования. Такой подход называется обратным проецированием с фильтрацией. Он имеет два математических метода реализации: метод свертки в пространственном домене и метод преобразований Фурье в частотном домене. Остановимся на них подробнее.
3.2.1. Метод свертки
Размытие реконструированных изображений, имеющее место при МПОП, в значительной степени устраняется с помощью свертки, в которой функция, называемая "ядром", сворачивается с данными проекции и полученный результат подвергается обратному проектированию. Применение ядра является математической операцией, которая существенно удаляет 1/r особенность, беря некоторую часть отсчетов из соседних пикселей и перенося их в центральный пиксель интереса. Формально математически свернутое изображения 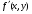 записывается в виде записывается в виде
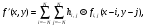 (7.4) (7.4)
где 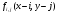 – пиксельная плотность счета в локализации – пиксельная плотность счета в локализации 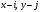 в набранной проекции; hi,j – весовой фактор ядра свертки. в набранной проекции; hi,j – весовой фактор ядра свертки.
Для уменьшения статистических флуктуаций в ЯМ широко используется введенный ранее (глава 5) девятиточечный сглаживающий фильтр (3 × 3 размер). Смысл этого приема заключается в усреднении числа отсчетов в каждом пикселе в соответствии с числом отсчетов в соседних пикселях в матрице набора данных. Пример применения девятиточечного сглаживающего фильтра показан на рис. 7.11. Пусть необходимо сгладить в матрице набора пиксель с числом отсчетов 5. Предположим, что свертывается 3 × 3 матрица набора (такого же размера как матрица ядра), центрированная на выбранном пикселе. Каждая исходная величина пикселя этой матрицы умножается на соответствующий весовой фактор и результаты суммируются. Весовые факторы вычисляются делением индивидуальных пиксельных значений матрицы ядра на сумму всех пиксельных значений матрицы. В результате данной операции значение числа отсчетов в пикселе изменилось с 5 на 3. Таким же образом сглаживаются значения, накопленные во всех пикселях матрицы набора.
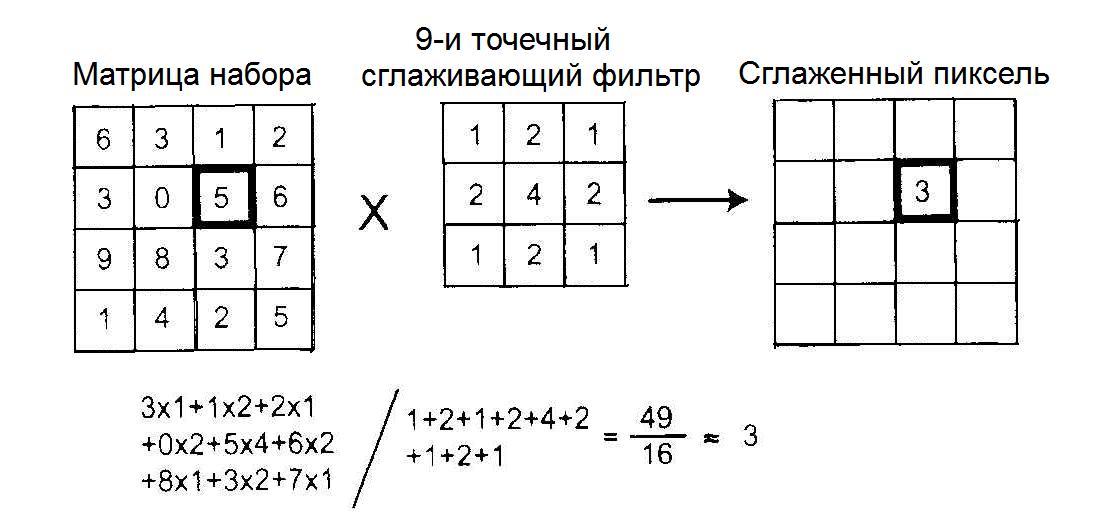
Рис. 7.11. Иллюстрация методики сглаживания в пространственном домене с девятиточечным сглаживающим ядром [8]
Пространственное ядро, описанное выше и имеющие все взвешивающие факторы положительными, уменьшает шум, но одновременно ухудшает пространственное разрешение. Резкие края в исходном изображении размываются в результате такой операции сглаживания.
Другой вид ядра, часто используемый в пространственном домене, состоит из узкого центрального пика с положительными и отрицательными значениями по обеим сторонам пика (рис. 7.12).
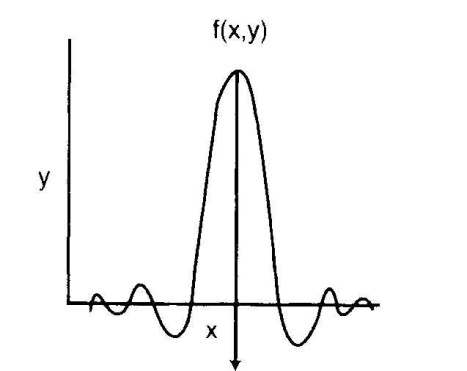
Рис.7.12. Фильтр в пространственном домене. Отрицательные значения по бокам центрального максимума уменьшают нежелательные вклады, которые ведут к размытию реконструированного изображения [8]
Когда этот так называемый "обостряющий края" фильтр применяется центрально к пикселю для корректировки, отрицательные значения нейтрализуют или исключают вклад от плотности отсчетов в соседних пикселях. Такая процедура повторяется для всех пикселей, после чего скорректированные данные включаются в процесс обратного проецирования. Метод воспроизводит первоначальное изображение с лучшим пространственным разрешением, но увеличивается шум. Отметим, что размытие, обусловленное МПОП, данным методом устраняется, однако шум, присущий набору данных вследствие ограничений пространственного разрешения визуализационного устройства не уменьшается, а скорее увеличивается.
3.2.2. Метод преобразований Фурье
Метод преобразований Фурье частично рассматривался в главе 5 применительно к получению плоскостных изображений. Будет полезно еще раз вернуться к обсуждению его особенностей применительно к ОФЭКТ.
Данные ЯМ, полученные в пространственном домене (рис. 7.13,а), могут быть выражены в частотном домене как сумма рядов синусоидальных волн разной амплитуды, пространственной частоты и фазовых сдвигов (рис. 7.13,б). Таким образом, данные каждой строки и каждого столбца матрицы набора возможно представить в виде подобной суммы. Процесс определения амплитуд синусоидальных волн называется преобразование Фурье, а процесс преобразования из частотного домена в пространственный называется обратным преобразованием Фурье.
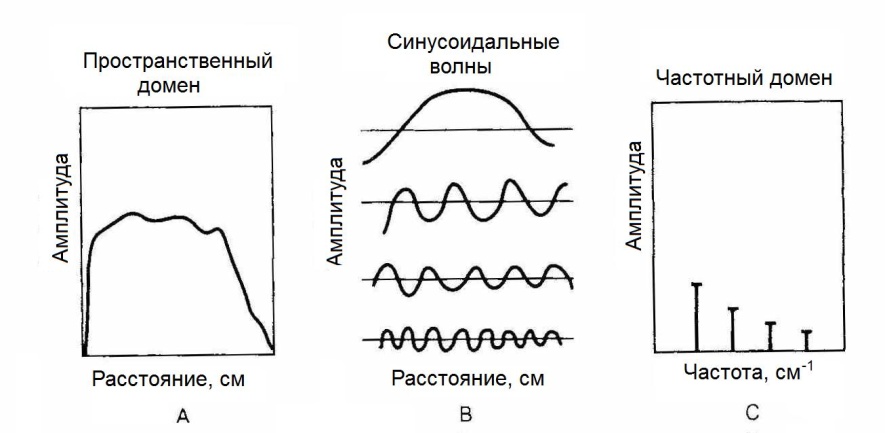
Рис. 7.13. Представление объекта в пространственном и частотном доменах [8]
Реконструкция изображений методом Фурье может проводиться двумя способами: или непосредственно, или используя фильтрацию. В прямом подходе преобразования Фурье отдельных набранных проекций выполняются в полярной системе координат частотного домена. Полученные результаты затем используются для расчета значений в декартовой системе координат. К последним для получения изображения применяется уже обратное преобразование Фурье. Такой способ не есть, строго говоря, обратное проецирование и редко используется для реконструкции изображений из-за большой трудоемкости.
Более удобным способом реконструкции является фильтрованное обратное проецирование, используя метод Фурье (ФОПФ, англ. FBP). В этом случае для устранения размытия, описываемого функцией 1/r, которое возникает при простом обратном проецировании, применяется фильтрация. Фильтрация выполняет модуляцию амплитуд разных частот, сохраняя широкие структуры изображения, представляемые низкими частотами, и уменьшая амплитуду или совсем устраняя мелкие структуры, представляемые высокими частотами. Если обозначить двумерное преобразование Фурье функции f(x,y) (см. формулу (7.4)) через F(νx,νy), а функцию пропускания фильтра через H(ν), то процедура фильтрации математически записывается в виде
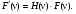 (7.5) (7.5)
Далее к 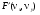 применяется обратное преобразование Фурье для получения фильтрованных проекций, которые затем обратно проецируются. Изображения, получаемые методом фильтрованного преобразования Фурье примерно эквивалентны изображениям, получаемым методом свертки, но современные компьютеры, применяя методику быстрых преобразований Фурье, выполняют реконструкцию изображений методом фильтрованных преобразований Фурье значительно быстрее. Наиболее широко используемые в ЯМ фильтры были рассмотрены ранее в главе 5. применяется обратное преобразование Фурье для получения фильтрованных проекций, которые затем обратно проецируются. Изображения, получаемые методом фильтрованного преобразования Фурье примерно эквивалентны изображениям, получаемым методом свертки, но современные компьютеры, применяя методику быстрых преобразований Фурье, выполняют реконструкцию изображений методом фильтрованных преобразований Фурье значительно быстрее. Наиболее широко используемые в ЯМ фильтры были рассмотрены ранее в главе 5.
3.3. Метод итеративной реконструкции
Основной принцип итеративной реконструкции заключается в сравнении измеренного изображения с оцененным изображением. Сравнение повторяется, пока не будет достигнуто удовлетворительное согласие. На практике первоначальная оценка создается из отдельных пикселей в проекции реконструированной матрицы такого же размера как матрица набора, и далее проекция сравнивается с измеренным изображением. Если оцененные пиксельные значения в проекции меньше или больше чем измеренные значения, тогда каждое пиксельное значение подправляется по отношению к другим пикселям в проекции для получения новой версии оцениваемой проекции. Последняя затем сравнивается с измеренной проекцией. Процесс повторяется до тех пор пока, не будет получено удовлетворительное согласие между оцениваемом и истинным изображением. Схематическое представление реконструкции изображений итерационным методом показано на рис. 7.14. Итерационный метод связан с большим количеством вычислений, поэтому до последнего времени редко применялся на практике. С появлением в клиниках мощной компьютерной техники ситуация изменилась, особенно популярным этот метод стал при реконструкции изображений в ПЭТ.
В качестве начального приближения для оценочного сравнения часто выбирается однородное изображение (например, все пиксели равны 0, 1 или средней величине). Изображение далее разворачивается (unfolded) в ряд проекций. Этот процесс, в противоположность к обратному проектированию, называется "прямое проектирование". В нем проводится определение взвешенной суммы активностей во всех пикселях в проекции поперек оцененного изображения. Как показано на рис. 7.15, проекция qi в оцененном изображении рассчитывается в виде
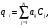 (7.6) (7.6)
где Cj – число отсчетов (активность) в j-пикселе; aij – вероятность, что эмиссия из пикселя j будет зарегистрирована в i-проекции. Вес aij равен доли активности в j-пикселе от полной активности вдоль j-проекции.
Если pi есть измеренная проекция, то погрешность рассчитывается как разность (pi– qi) или как отношение pi/qi. Эта погрешность ((pi– qi) или pi/qi) в виде весовых факторов затем включается во все пиксели (N) вдоль i-проекции в соответствии с выражениями
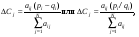 (7.7) (7.7)
где ΔCj– погрешность, вводимая в j-пиксель i-проекции. Отметим, что при расчете погрешности учитываются только пиксели, принадлежащие данной проекции. Однако, в действительности, все пиксели изображения имеют конечную вероятность создать вклады в отсчеты любого пикселя в любой проекции, и поэтому расчет погрешностей является время затратным процессом.
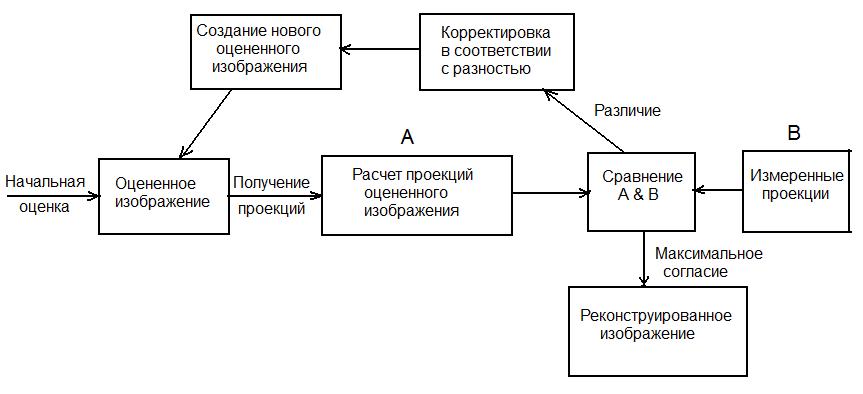
Рис. 7.14. Принципиальная схема итерационного метода реконструкции изображений
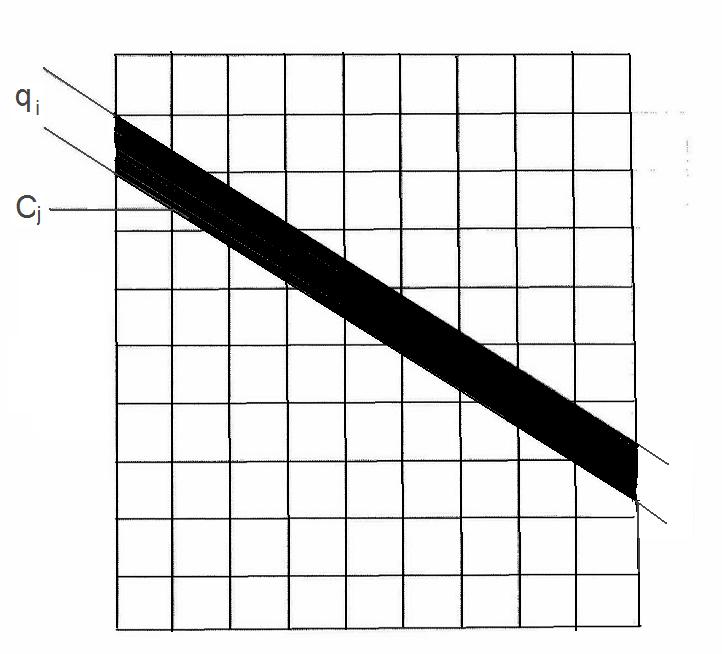
Рис.7.15. Иллюстрация расчета проекции qiоцененного изображения, представляющей сумму отсчетов во всех пикселях Cj
На практике используются три способа расчета и применения поправок на наличие погрешностей. В методике простой итерации (точка-за-точкой) рассчитываются погрешности, обусловленные всеми пикселями из всех проекций, проходящих через конкретный пиксель, и результаты используются для корректировки числа отсчетов в этом пикселе, прежде чем перейти к следующему пикселю. В методике проекция-за-проекцией погрешность рассчитывается для каждой проекции, и изображение корректируется перед переходом к следующей проекции. В методике одновременной итерации погрешность определяется для всех проекций и затем используется для одновременной корректировки изображения.
Отличительные особенности итерационного метода реконструкции изображений по сравнению с методом фильтрованного обратного проецирования заключаются в практическом отсутствии в изображениях артефактов, что достаточно часто наблюдается при реконструкции изображений последним методом, и в лучшем значении отношения сигнал/шум в низкоконтрастных областях.
|
 Скачать 9.62 Mb.
Скачать 9.62 Mb.




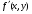 записывается в виде
записывается в виде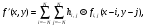 (7.4)
(7.4)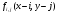 – пиксельная плотность счета в локализации
– пиксельная плотность счета в локализации 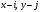 в набранной проекции; hi,j – весовой фактор ядра свертки.
в набранной проекции; hi,j – весовой фактор ядра свертки.


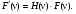 (7.5)
(7.5)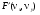 применяется обратное преобразование Фурье для получения фильтрованных проекций, которые затем обратно проецируются. Изображения, получаемые методом фильтрованного преобразования Фурье примерно эквивалентны изображениям, получаемым методом свертки, но современные компьютеры, применяя методику быстрых преобразований Фурье, выполняют реконструкцию изображений методом фильтрованных преобразований Фурье значительно быстрее. Наиболее широко используемые в ЯМ фильтры были рассмотрены ранее в главе 5.
применяется обратное преобразование Фурье для получения фильтрованных проекций, которые затем обратно проецируются. Изображения, получаемые методом фильтрованного преобразования Фурье примерно эквивалентны изображениям, получаемым методом свертки, но современные компьютеры, применяя методику быстрых преобразований Фурье, выполняют реконструкцию изображений методом фильтрованных преобразований Фурье значительно быстрее. Наиболее широко используемые в ЯМ фильтры были рассмотрены ранее в главе 5.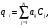 (7.6)
(7.6)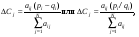 (7.7)
(7.7)
