Физика ядерной медицины
 Скачать 9.62 Mb. Скачать 9.62 Mb.
|
Накопление рассеянного излученияПри визуализации пациента гамма-камерой комптоновское рассеяние не только ослабляет первичное излучение, но также создает значительное количество нежелательного рассеянного излучения. Эти рассеянные фотоны могут пройти через коллиматор камеры, и если их не дискриминируют по энергии входные "ворота" ААИ, то они создадут свой вклад в общее число зарегистрированных отсчетов. В типичном случае (для 140-кэВ фотонов) ширина окна входного дискриминатора равна ± 10 %, что позволяет фотонам, рассеянным на угол < 500, войти в число зарегистрированных вместе с первичными. Фотоны могут перед попаданием в детектор испытать многократное рассеяние, и если сумма углов рассеяния ≤ 500, то и они могут пройти через окно дискриминатора (рис. 6.5). 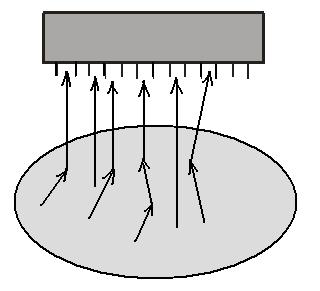 Рис. 6.5. Пример разных фотонов (первичных, однократно рассеянных и многократно рассеянных фотонов), которые могут создать вклад в полное количество фотонов, регистрируемых гамма-камерой Оценки показывают, что общий вклад в скорость счета, создаваемый рассеянными фотонами, может достигать 40 %. Такая геометрия часто называется геометрией широкого пучка. В этом случае прохождение фотонов через материал уже не описывается простой экспоненциальной функцией типа (6.1). График зависимости коэффициента прохождения фотонов от толщины материала в полулогарифмическом масштабе (рис. 6.6) обнаруживает "плечо" на небольших толщинах и становится близким к прямой линии только на больших толщинах. Для учета рассеянного излучения в геометрии широкого пучка вводится понятие фактора накопления B(x), который определяется следующим образом: 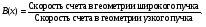 (6.15) (6.15)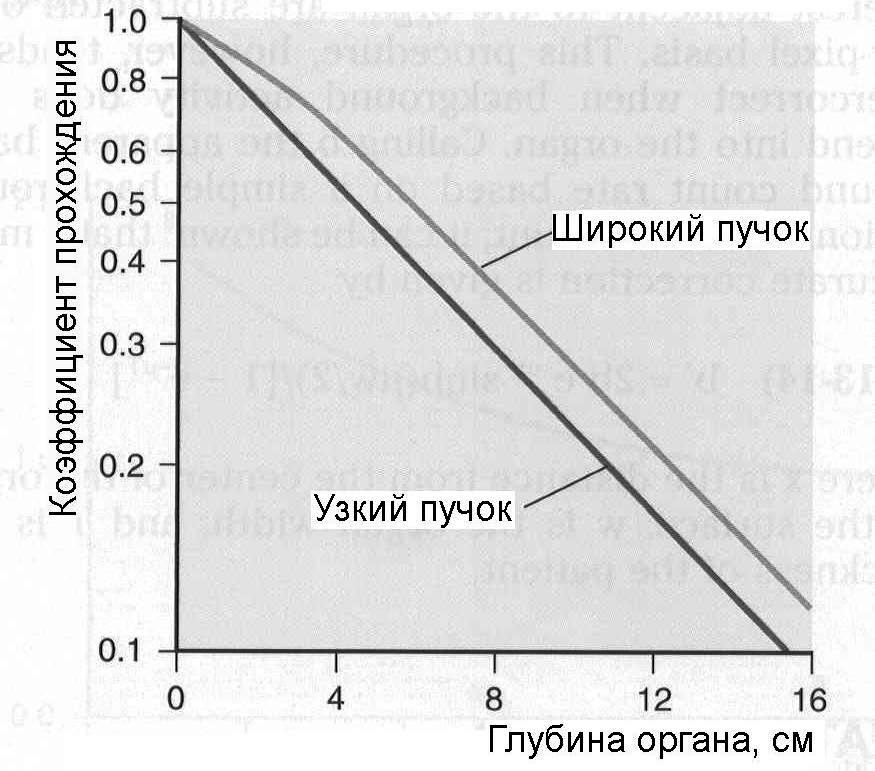 Рис. 6.6. Зависимость коэффициента прохождения 140-кэВ фотонов от толщины материала в геометриях "узкого" и "широкого" пучков [3] Типичная зависимость фактора накопления от толщины материала показана на рис. 6.7. При очень малой толщине x фактор накопления B ≈ 1, с увеличением толщины B также увеличивается, стремясь к асимптотическому значению 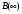 на больших толщинах. Величина на больших толщинах. Величина 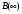 зависит от энергии фотонов, ширине энергетического окна ААИ, типа коллиматора и относительно мало чувствительна к размеру источника. Аппроксимационная формула для расчета скорости счета в геометрии широкого пучка была предложена в работе [6] в виде: зависит от энергии фотонов, ширине энергетического окна ААИ, типа коллиматора и относительно мало чувствительна к размеру источника. Аппроксимационная формула для расчета скорости счета в геометрии широкого пучка была предложена в работе [6] в виде: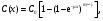 (6.16) (6.16)где значение μ, дающее наилучший результат обычно близко к линейному коэффициенту ослабления для узкого пучка, но может изменяться в зависимости от поперечной площади источника и других факторов [6]. Формулу (6.16) рекомендуется применять при небольшой толщине источника. Если же источник толстый, то в (6.16) дополнительно вводится поправочный фактор g (см. (6.12)): 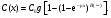 (6.17) (6.17)Аккуратное определение активности в типичном варианте требует сопряженных (парных) измерений, например, в верхнем и нижнем положениях гамма-камеры. Соответствующие скорости счета Ca и Cp равны 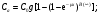 (6.18) (6.18)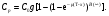 (6.19) (6.19)Отношение скоростей счета в этих позициях равно: 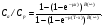 (6.20) (6.20)С помощью компьютера ищется значение x, при котором удовлетворяется уравнение (6.20). Далее, имея значение x, из (6.18) и (6.19) находится величина C0, и наконец, по формуле (6.3) определяется искомая активность. Данный метод определение активности получил название "метод фактора накопления". Парные измерения, применяемые в этом методе, существенно упрощается при использовании гамма-камер с двумя противоположно расположенными детекторами. Учитывая, что параметры метода 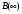 и μ чувствительны к условиям получения изображения, рекомендуется определять их экспериментально на фантомах, моделирующих клиническую ситуацию. и μ чувствительны к условиям получения изображения, рекомендуется определять их экспериментально на фантомах, моделирующих клиническую ситуацию.Контрольные вопросы
|
