Физика ядерной медицины

• Название: Физика ядерной медицины
• Анкор: Part 1.docx
• Дата: 28.01.2017
• Размер: 9.62 Mb.
• Имя файла: Part 1.docx
• Тип: Документы; #616
• страница: 26 из 40

Фильтрация цифрового изображения

Цифровой фильтр является математической операцией, совершаемой над сигналом (или изображением), в которой выборочно ослабляются или усиливаются различные частоты этого сигнала. Фильтрация может быть применена как в пространственном домене в виде свертки функции фильтра с сигналом, так и в частотном домене через трансформацию Фурье функций фильтра и сигнала, их перемножением и последующем расчетом обратного преобразования Фурье результата перемножении. В этом разделе рассматриваются некоторые виды цифровых фильтров и обсуждаются методы фильтрации, наиболее часто применяемые к сцинтиграммам в ЯМ. За основу изложения взята обзорная работа [4].

4.1. Линейная и нелинейная фильтрация

Изображения, полученные через процессинг с линейными фильтрами, представляют линейную комбинацию значений в различных пространственных позициях нефильтрованного изображения. В этом разделе обсуждаются, главным образом, линейные фильтры, хотя на практике используется и некоторое количество нелинейных фильтров. Как пример, можно привести медианную фильтрацию, заменяющую значение в каждом пикселе изображения медианным значением группы пикселей, окружающих конкретный пиксель. Разработан также ряд мощных нелинейных методов фильтрации, авторы которых пробуют смоделировать стохастическую природу измеряемых изображений [3, 5, 6].

4.2. Стационарные и нестационарные фильтры

В стационарных цифровых фильтрах делаются допущения, что случайный шум и размытие системой являются инвариантными в пределах изображения. Другими словами, фильтры не подстраиваются под локальные вариации в отношении сигнал-шум в разных местах изображения. Эти допущения, строго говоря, не соответствуют реальной ситуации, так как размытие системой (PSF) зависит от геометрии источника и пуассоновское распределение шума меняется в пределах изображения. Тем не менее, данные допущения, как правило, делаются, потому что реализация стационарных фильтров проще с вычислительной точки зрения. Применение нестационарных фильтров является более сложной задачей, однако они имеют преимущество в отношении учета локальных характеристик изображения. В качестве примера приведем фильтр, который подавляет шум в низкочастотном диапазоне и усиливает в высокочастотном.

4.3. Низкочастотные фильтры и восстанавливающие фильтры

Низкочастотные фильтры (иногда называемые сглаживающими фильтрами) используются для уменьшения статистических флуктуаций сигнала или изображения. Этот вид фильтрации может быть применен как в пространственном, так и в частотном доменах. В пространственном домене низкочастотная фильтрация выполняется с помощью свертки функции фильтра с сигналом. На рис. 5.10 показан пример применения пятиточечного биноминоминального сглаживающего фильтра к одномерной последовательности данных. Центр фильтра передвигается от элемента к элементу в ряде данных. Фильтрованное значение каждого элементы генерируется как одна девятая ( обратная к сумме 1-2-4-2-1) от взвешенной суммы значений фильтра, умноженных на последовательность данных.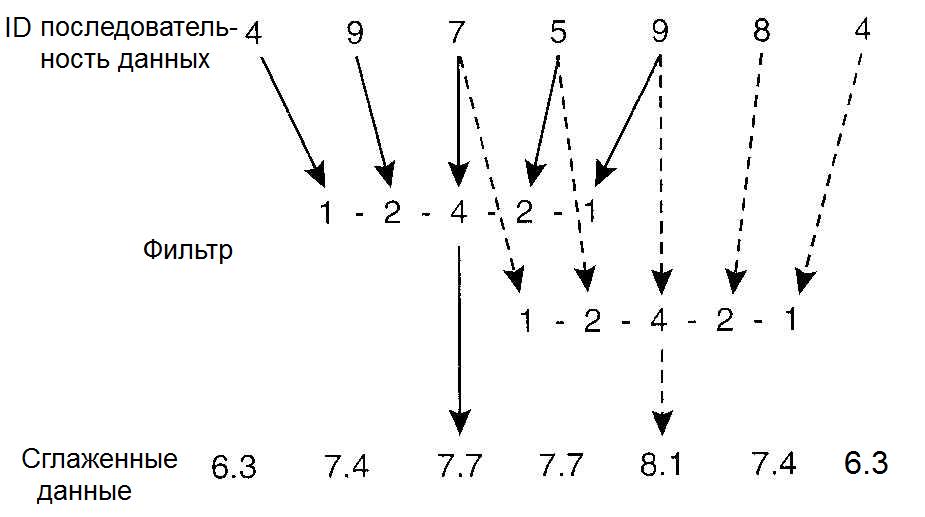

Рис.5.10. Пример применения 1-2-4-2-1 биноминального сглаживающего фильтра [4]
В рассматриваемом примере краевые точки рассчитываются "обертыванием" фильтра вокруг противоположной стороны последовательности. В случае двумерного пространственного домена низкочастотный фильтр применяется аналогичным образом. Как правило, тогда используется девятиточечная биноминальная функция размытия, имеющая следующие значения: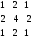


В частотном домене низкочастотный фильтр не трогает низкие частоты изображения и то же время ослабляет высокие частоты. Амплитуда частотного домена низкочастотного фильтра никогда не превышает 1,0 и уменьшается с увеличением частоты.

Наиболее часто в ЯМ применяется фильтр Баттеруорта, описываемый следующим уравнением: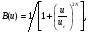

(5.15)

где u – частота; u_c – пороговая частота (частота, при которой амплитуда фильтра равна 0,5); N_c– порядок фильтра, который определяет насколько быстро амплитуда фильтра стремится к нулю. На рис. 5.11 приводятся графики фильтра Баттеруорта для разной пороговой частоты, а на рис. 5.12 показаны изображения печени в фантоме Алдерсона, обработанные фильтром Баттеруорта.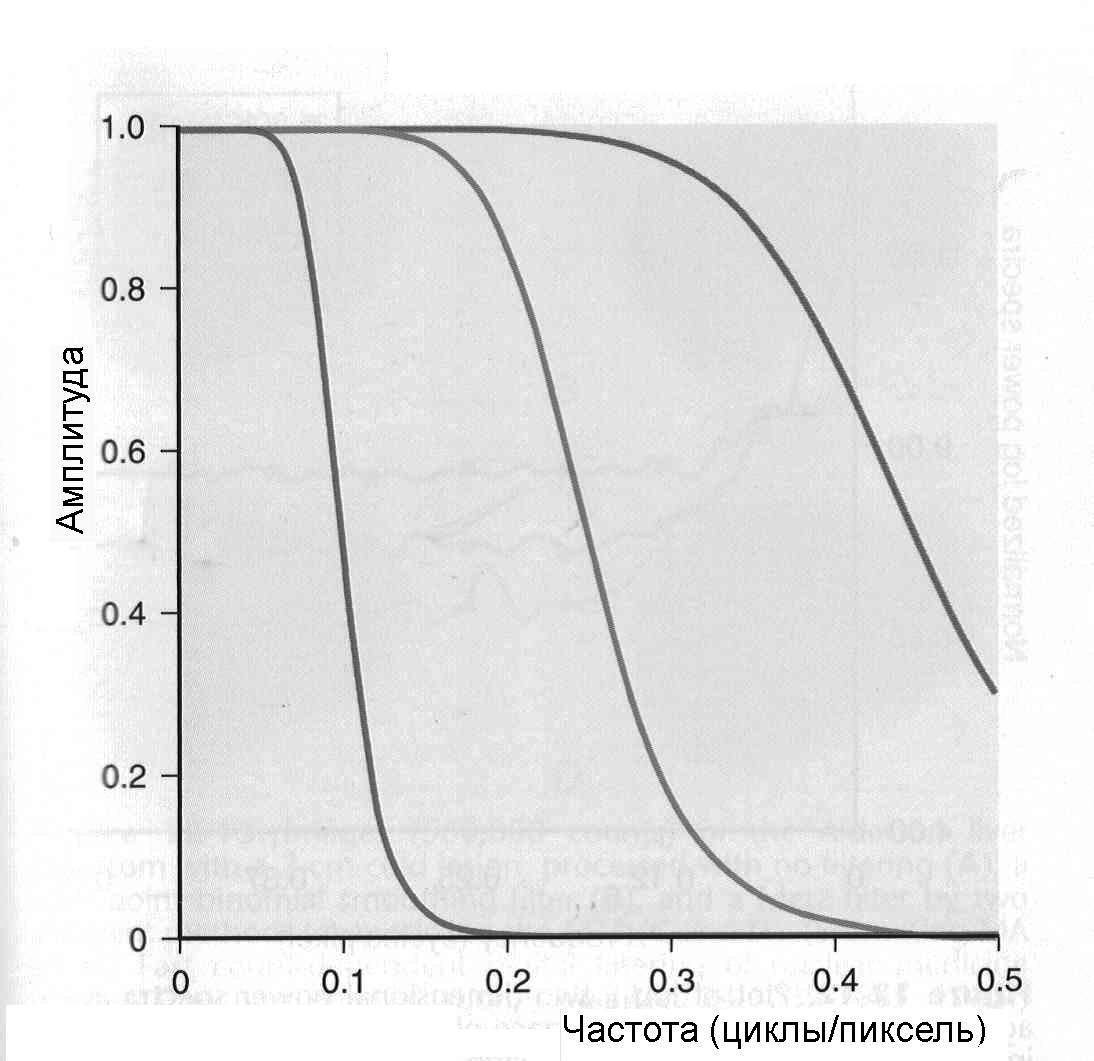


Рис.5.11. Зависимость амплитуды фильтра Баттеруорта четвертого порядка от частоты для граничных частот, равных 0,1, 0,25 и 0,45, умноженных на частоту Найквиста [4]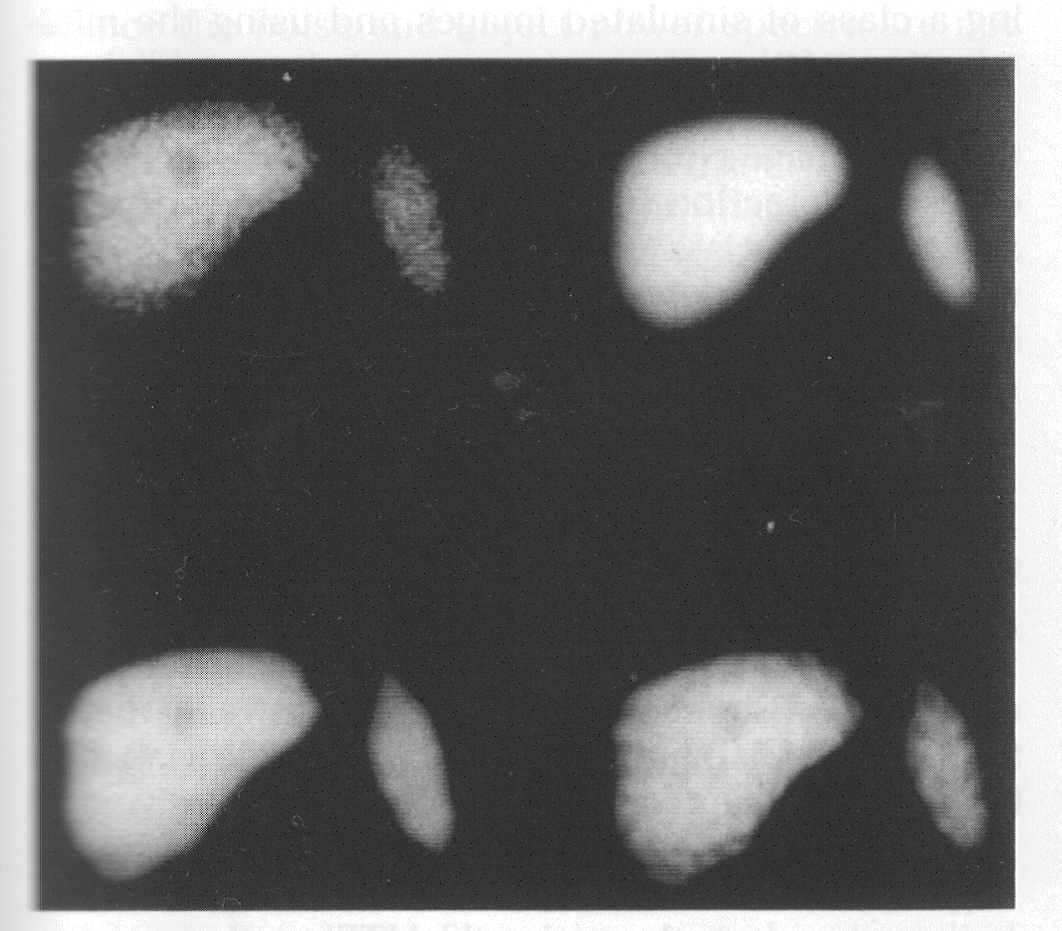



Рис.5.12. Моделированные изображения печени и селезенки (50000 полное число отсчетов), отфильтрованные тремя фильтра Баттеруорта (рис. 5.11): верх слева – нефильтрованное; верх справа -- пороговая частота равна 0,1; низ слева – пороговая частота равна 0,25; низ справа – пороговая частота равна 0,45 [4]
Из модели изображения, описываемой уравнением (5.13), видно, что зарегистрированное изображение g(i,j) ухудшается из-за размытия камеры, моделируемого как свертка изображения с PSF, и из-за шума. Проблема реконструкции (восстановления) изображения заключается в получении изображения, которое регистрировалось бы идеальной гамма-камерой, т.е. без размытия и шума. Это идеальное изображение, обозначенное f(i,j) в уравнении (5.13), будем называть объектным изображением. Фильтр реконструкции представляет математическую операцию, выполняемую с измеренным (зарегистрированным) изображением для получения объектного изображения. Восстановительная фильтрация отличается от низкочастотной фильтрации тем, что она не только подавляет шум, но также уменьшает эффекты искажения, связанные с системным размытием (они вызываются как особенностями отклика камеры, так и рассеянием излучения).

Одно из решений проблемы реконструкции изображения состоит в применении обратного фильтра в виде: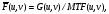

(5.16)

где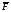– оценка преобразования Фурье объектного изображения; MTF – модуляционная передаточная функция.

Уравнение (5.16) известно как определение обратного фильтра, так как преобразование Фурье измеренного изображения умножается на обратную величину модуляционной передаточной функции). Оценка истинного изображения объекта 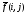может быть отсюда рассчитана через операцию обратного преобразования Фурье. Однако эта операция имеет тенденцию к излишнему усилению шума в изображении. С другой стороны известно [7], что высокочастотным компонентом изображения является по преимуществу шум, поэтому желательно ослабить этот компонент изображения. Таким образом, в частотном домене за восстановительным фильтром должна следовать инверсия передаточной функции в диапазоне низких частот, где мощность сигнала выше, чем мощность шума, и затем спадать до нуля в области высоких частот, где преобладает шум.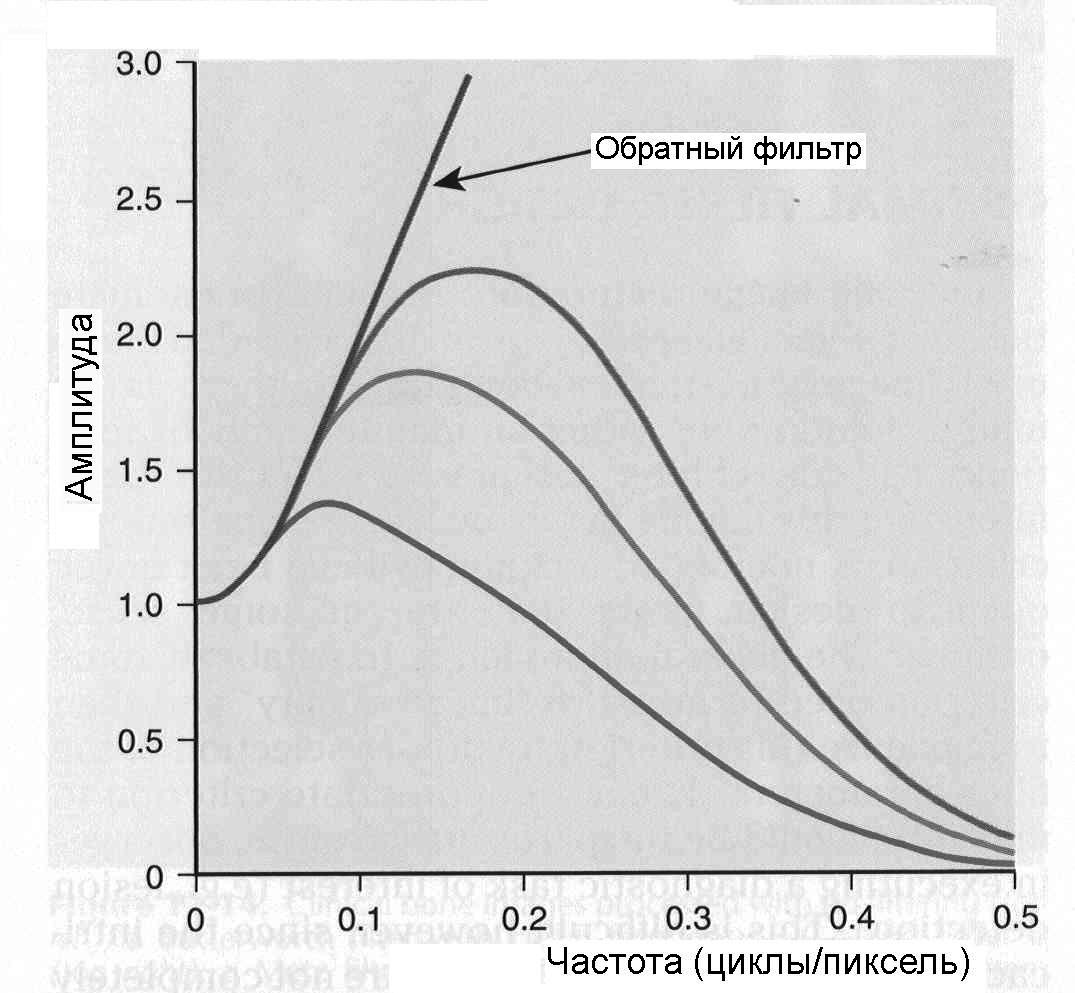



Рис. 5.13. Зависимость абсолютных значений обратного фильтра (1/MTF) и трех фильтров реконструкции Метца от частоты для разных уровней шума [4]
Частота, при которой фильтр должен приостановить обращение MTF и начать cпадание к нулю (пороговая частота) зависит от относительного количества шума в изображении. Следовательно, при увеличении шума в изображении пороговая частота фильтра должна понижаться, тем самым отфильтровывая больше шума. На рис. 5.13 нарисованы графики обратного MTF фильтра и семейства фильтров реконструкции Метца (см. ниже), оптимизированных для различных уровней шума.