Физика ядерной медицины

• Название: Физика ядерной медицины
• Анкор: Part 1.docx
• Дата: 28.01.2017
• Размер: 9.62 Mb.
• Имя файла: Part 1.docx
• Тип: Документы; #616
• страница: 25 из 40

Некоторые математические преобразования, используемые при обработке изображений

1. Анализ в частотном пространстве

Изображения в ЯМ представляют собой пространственные распределения зарегистрированной эмиссии р/н. Такое способ часто называют представлением в пространственном домене (области). Вместе с тем нередко возникает необходимость преобразовать данные изображения в так называемый частотный домен. Это преобразование основывается на фундаментальном факте, что любую математическую функцию можно представить в виде суммы синусоидальных и косинусоидальных функций различной частоты и различных фаз (термин фаза относится к начальной точке этих функций) (Фурье, 1807 г.). Такая математическая операция называется преобразование Фурье, при этом исходная информация преобразуется в другую более удобную форму. Как только это сделано, изменяются перспективы исследований, появляется возможность более глубокого понимания объекта. Особенно важное значение такое преобразование приобретает при модификации и фильтрации изображений.

Имея математическое описание изображения в виде двумерной функции 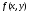, ее двумерное Фурье преобразование можно выразить в следующем виде: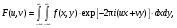

(5.3)

где u и v – декартовые координаты в комплексной плоскости; 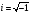(уравнение Эйлера устанавливает: ).

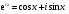Обратное преобразование Фурье имеет вид: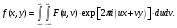

(5.4)

Таким образом, измеренное изображение может быть представлено в виде зарегистрированных отсчетах в каждой пространственной позиции или в виде амплитуд и фаз для каждой частоты. Высокочастотная составляющая изображения в частотном домене содержит информацию о краях и быстро изменяющихся районах (т.е. с большой разницей плотности счета между близко расположенными объектами), в то время как низкочастотная составляющая содержит информацию о районах с относительно медленно меняющейся плотностью счета. На рис. 5.7 показан пример преобразования Фурье поперечного изображения головного мозга. Единицы измерения вдоль осей u и v обычно являются число циклов на сантиметр или циклов на пиксель.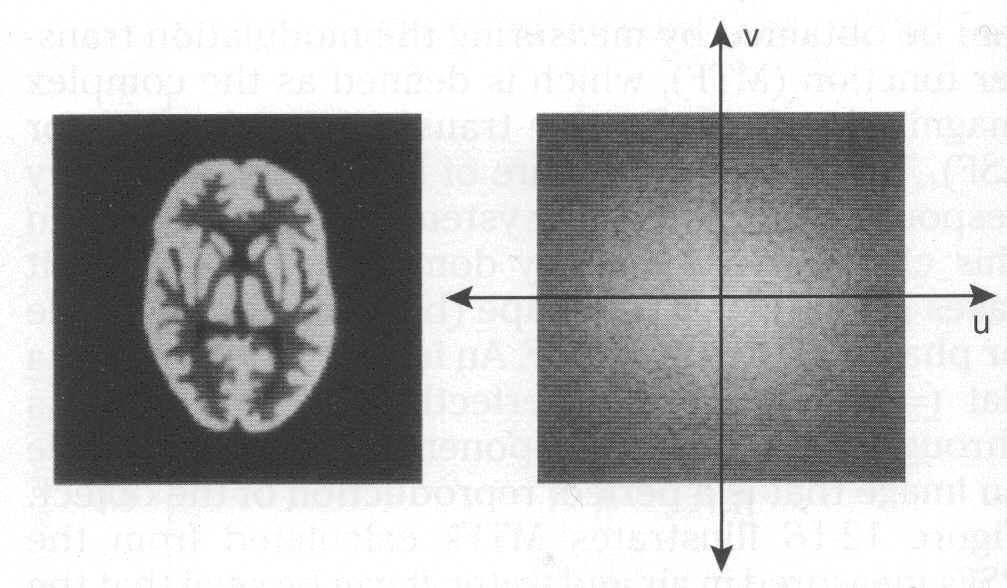



Рис. 5.7. Поперечное изображение мозга (а) и его соответствующее двумерное преобразование Фурье [4]

3.2. Теория выборки

Для каждого фотона, испытывающего взаимодействие в детекторе гамма-камеры, генерируется три аналоговых сигнала. Два сигнала представляют X-, Y- пространственные координаты точки взаимодействия фотона, и третий сигнал указывает, какая энергия была поглощена при взаимодействии. Теоретически зарегистрированное изображение есть непрерывная функция, являющаяся проекцией 3-мерного распределения р/н внутри пациента на двумерную плоскость передней поверхности гамма-камеры. Однако так как цифровой компьютер работает с дискретными числами, непрерывные функции, представляющие изображения, подвергаются выборке (англ. sampling) или делению на 64 × 64, 128 × 128, 256 × 256 матриц или дискретных пиксельных элементов. Эта операция выполняется с помощью конвертирования аналоговых X-, Y-позиционных сигналов в дискретные величины с помощью АЦК (см. главу 3).

Возникает вопрос: полноценно ли выборочная версия функции представляет ее непрерывную форму, и не происходит ли при таком преобразовании потеря информации? Ответ на этот вопрос дает теорема выборки. Для простоты анализа рассмотрим одномерную функцию f(x). В теореме выборки доказывается, что если преобразование Фурье функции f(x) является ограниченным в частотном домене, т.е. если F(u) равно нулю для всех частот выше чем определенная частота u_c, тогда непрерывная функция f(x) может быть однозначно определена из знания N выборочных значений: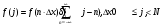

(5.5)

где пространственный интервал выборки (или размер пикселя) равен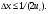

(5.6)

В уравнении (5.5) j относится к номеру выбранного значения, например, f(5) означает пятое выбранное значение. Функция δ(x) определена следующим образом: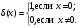

(5.7)

Если условие (5.6) выполняется, то функция f(x) полностью восстанавливается из ее выборки, используя уравнение: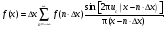

(5.8)

Уравнение (5.6) следует, что теорема выборки накладывает ограничение на максимальное расстояние между выборочными образцами (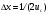). Другими словами, выборочные интервалы должны быть, по крайней мере, составлять обратное величину для двух высших частот функции интереса. Обратная величина Δxчасто называется частотой выборки, а (1/(2·Δx) частотой Найквиста.

Что случится, если функция выбирается с максимальным пространственным интервалом (размером пикселя) большим, чем 1/(2u_c)? В этом случае первоначальная функция не будет полностью восстанавливаться из ее выборочных значений, и восстановленная функция будет содержать повышенные частоты под видом пониженных частот. Этот феномен получил название смещение (англ. aliasing).

3.3. Свертка функций

Свертка функций – это важнейшее математическое понятие, которое используется почти во всех областях науки и техники, в том числе, оно широко применяется для оценки систем изображения и для процессинга цифровых изображений. Свертка двух функций – это математическая операция двух функций h(x) и f(x), порождающая третью функцию g(x), которая может рассматриваться как модифицированная версия одной из первоначальных, например, после операций осреднения или сглаживания. Свертка h(x) и f(x) записывается как h∗f (символ звездочки). Для непрерывных функций она определяется как интеграл от произведения двух функций после того, как одна реверсируется и смещается. По существу, это особый вид интегрального преобразования: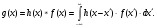

(5.9)

Операция свертки иллюстрируется на рис. 5.8 для двух функций, заданных в виде прямоугольных импульсов разной длительности.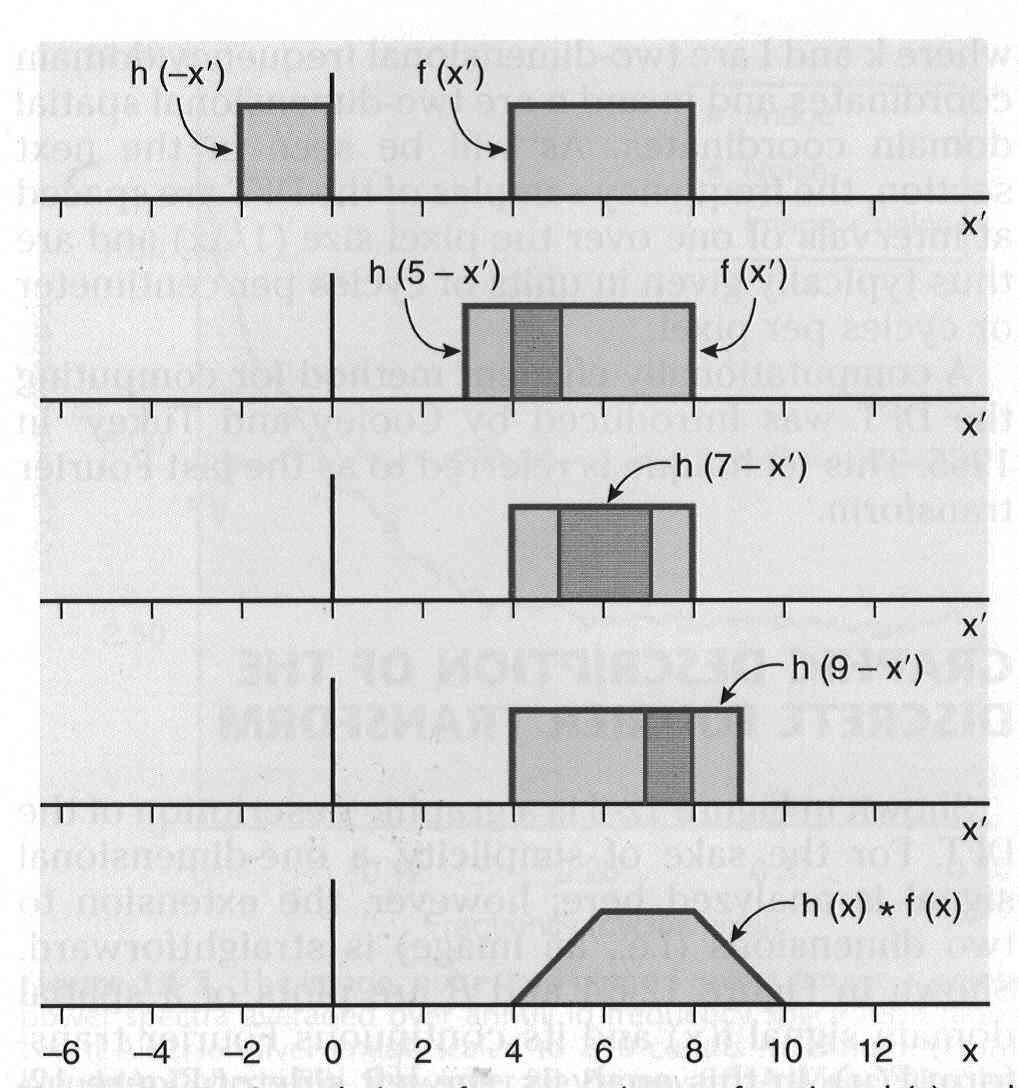



Рис. 5.8. Пример свертки двух непрерывных функций h(x) и f(x). Более темным цветом показана площадь, равная интегралу (5.9) при разных значениях x (адаптировано из [4])
Одномерная дискретная свертка двух дискретных функций h(i) и f(i) длиной N определяется как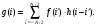

(5.10)

С точки зрения вычислительного процесса более легким и быстрым способом расчета свертки двух функций является использование теоремы свертки. В этой теореме доказывается, что свертка двух функций эквивалентна перемножению их преобразований Фурье в частотном пространстве. Таким образом, уравнение свертки (5.9) можно выразить в виде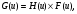

(5.11)

где H(u) и F(u) – преобразование Фурье функций h(x) и f(x) в частотном пространстве.

3.4. Дискретные преобразования Фурье

Для преобразования дискретной формы изображения в частотной пространство традиционно применяется дискретное преобразование Фурье (ДПФ, англ. DFT). Двумерное прямое и обратное дискретные преобразования Фурье для выборки N × N пикселей изображения [f(m,n)] записываются следующим образом: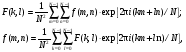

(5.12)

где k и l – координаты в двумерном частотном домене; m и n – координаты в двумерном пространственном домене.

На практике со второй половины прошлого века большинство расчетов в прямом и обратном преобразовании Фурье выполняется с помощью высокоэффективного метода "быстрого преобразования Фурье".

3.5. Графическое изображение дискретного преобразования Фурье

Для лучшего понимания ДПФ рассмотрим графическую иллюстрацию этого процесса, показанную на рис. 5.9. Для простоты проанализируем одномерный сигнал. На левой стороне рис. 5.9 представлены графики функций в пространственном домене и на правой стороне – в частотном домене.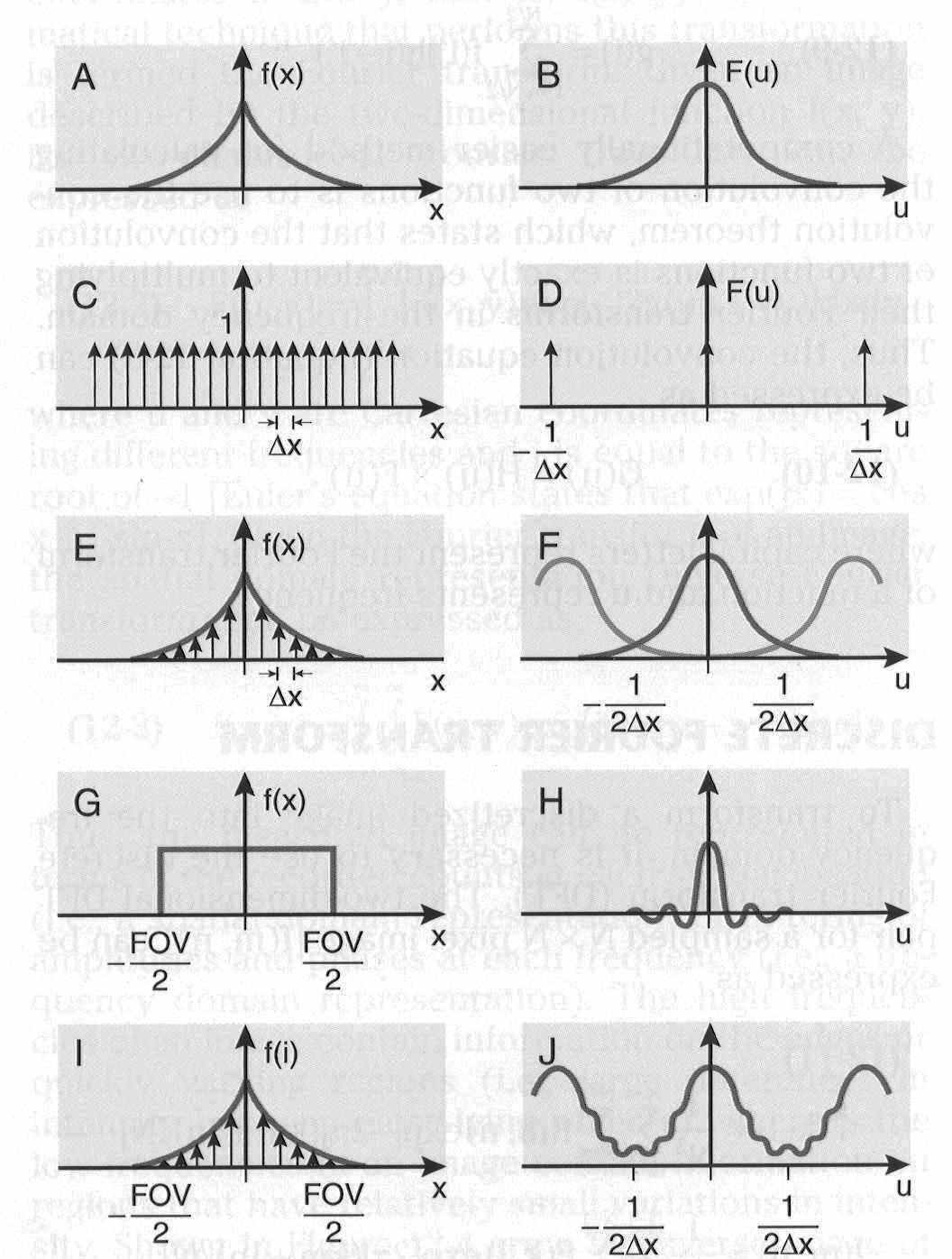


Рис. 5.9. Графическая иллюстрация дискретного преобразования Фурье [4]
На рис. 5.9,А и 5.9,В показаны графики сигнала f(x) и его непрерывного преобразованием Фурье F(u). Процесс выборки, как это следует из уравнения (5.5), выполняется умножением f(x) на бесконечную импульсную последовательность с интервалом между импульсами равном Δx (рис. 5.9,С). Преобразование этой последовательности также является бесконечной последовательностью с частотным интервалом равном 1/(Δx) (рис. 5.9,D). Выборочная функция f(n·Δx) показана на рис. рис. 5.9,E.

Из теоремы свертки известно, что перемножение в одном домене эквивалентно свертке в другом домене. Таким образом, преобразование Фурье f(n·Δx) есть просто функция F(u) (рис. 5.9,B), свернутая с бесконечной последовательность импульсов (рис. 5.9,D). Как можно видеть из рис. рис. 5.9,F, выборка функции порождает репликацию ее преобразования Фурье с периодом 1/(2Δx), и дополнительно наблюдается небольшой эффект наложения, так как репликации более высоких частот имеет тенденцию свертки в частотный диапазон исходной трансформации F(u).

Согласно теореме свертки, если f(x) не имеет частотного ограничения (т.е. F(u) ≠ 0 для |u| > u_c), то возникнет погрешности наложения. Эффект наложения можно уменьшить с помощью сужения интервала выборки (Δx). Дискретная функция, показанная на рис. 5.9,Е, является бесконечно длинной последовательностью. Для представления в цифровом компьютере требуется конечное число выборочных значений. Таким образом, необходимо усечение или оконное представление бесконечной последовательности. Этот шаг очень существенен в процессе выборки и выражается графически через перемножение f(n·Δx) (рис. 5.9,Е) с прямоугольным импульсом шириной, равной полю обзора камеры FOV (рис. 5.9,G). Усеченная выборочная последовательность f(i) показана на рис. 12.6,I. Преобразование Фурье прямоугольного импульса представляет синусоидальну функцию 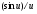(рис. 5.8,H).

Из теоремы свертки следует, что перемножение в пространственном домене эквивалентно свертке в частотном домене. Поэтому существенное усечение, которое было реализовано прямоугольным импульсом шириной, равной FOV, эквивалентно свертке выборочной частотной трансформанты с синусоидальней функцией, показанной на рис. 5.8,H. По этой причине частотная трансформация f(i) содержит небольшие пульсации, видимые на рис. 5.9.J. Дискретное преобразование Фурье выполняется выборкой функции, показанной на рис. 5.9.J, с интервалом выборки 1/ FOV в частотном диапазоне 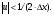Этот анализ наглядно выявил два эффекта, которые вызывает дискретное преобразование Фурье в отличие от непрерывного преобразования Фурье, а именно, частотное наложение и усечение.

3.6 Модель процесса визуализации

При анализе систем получения изображений бывает полезно сформировать модель процесса визуализации. Эту модель можно упростить, приняв допущения о линейности пространственной инвариантности изобразительной системы (т.е. влияние размытия (нечеткости) изображения гамма-камеры является одинаковым во всех частях изображения). Дополнительно, предположим, что статистические вариации или шум в изображении входят в процесс набора изображения аддитивно. Т.е. модель предполагает, что флуктуации, обусловленные шумом, включаются в изображение после того, как завершится процесс размытия изображения, связанный с физическими особенностями камеры. В результате этих упрощающих допущений процесс формирования изображения математически можно выразить в виде следующей модели: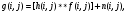

(5.13)

где ** означает дискретный двумерный оператор свертки; g(i,j) – размытие, измеренного изображения; h(i,j) – функция PSF системы изображения, которая характеризует размытие изображения в пространственной позиции (i,j); f(i,j) – идеальное изображение объекта (без размытия проекции распределения р/н внутри пациента).

Так как PSF системы изображения зависит от расстояния источник-детектор и от геометрии источника, h(i,j) (и H(u,v)) обычно моделируются для среднего расстояния источник-детектор и средней глубины источника в пациенте. Используя теорему свертки, данную модель процесса формирования изображения можно также выразить в частотном домене в виде: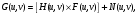

(5.14)

где H, F, N – обозначают двумерное преобразование Фурье соответствующих функций; u,v – координаты в частотном пространстве.