Физика ядерной медицины

• Название: Физика ядерной медицины
• Анкор: Part 1.docx
• Дата: 28.01.2017
• Размер: 9.62 Mb.
• Имя файла: Part 1.docx
• Тип: Документы; #616
• страница: 27 из 40

Проектирование оптимального фильтра

Проблема реконструкции изображения (оценка идеального изображения объекта, имея измеренное размытое изображение) относится к плохо-обусловленным задачам, т.е. она не имеет единственного решения. Целью проектирования фильтра является выбор "наилучшего" фильтра из бесконечного семейства фильтров на основе разумного критерия. Для решения проблемы был создан ряд методов, позволяющих спроектировать фильтры, являющихся оптимальными в некотором смысле. Общий подход заключается в выработке некоторого критерия, использующегося для измерения "качества фильтра, и последующего поиска максимума этого критерия на основе адекватного выбора параметров фильтра.

Наиболее уместным критерием здесь была бы максимизация способности оператора к выявлению в процессе диагностики патологических очагов. Выработка такого критерия является сверх трудной проблемой в силу недостаточного понимания всей сложности системы визуализации человека. Более разумный подход на данном этапе состоит в максимизации некоторого математического критерия, моделирующего качество изображения. Ниже рассматриваются два метода этого класса, наиболее широко применяемых в ЯМ для создания восстановительных фильтров.

5.1. Фильтр Метца

Фильтр Метца определяется как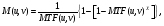

(5.17)

где X – параметр, который контролирует протяжение, на котором действует, прежде чем фильтр начинает подавлять высокочастотный шум.

Первый член в правой части уравнения (5.17) есть обратный фильтр, который доминирует на низких частотах, и второй член есть низкочастотный фильтр, который принуждает фильтр переключиться с восстановления на подавление шума. Как отмечено выше, частотный предел, начиная с которого, стартует низкочастотный фильтр, определяется значением X. Этот параметр зависит от полного числа отсчетов в изображении, которые необходимо отфильтровать. Причина для этого иллюстрируется на рис. 5.14, где показан спектр мощности двумерного изображения, усредненный по кольцам в частотном пространстве, для трех разных наборов печеночного фантома Алдерсона.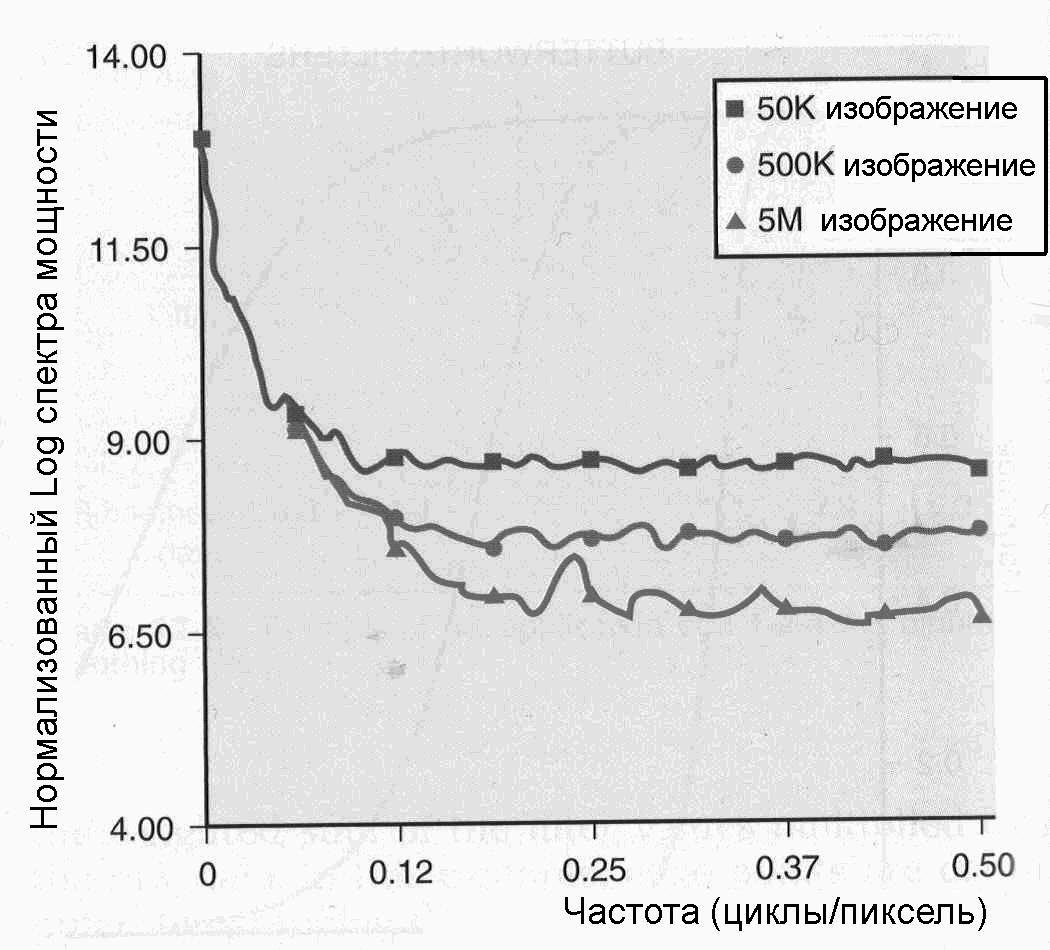



Рис. 5.14. Зависимость log₁₀ двумерного спектра мощности, усредненного по кольцам в частотном пространстве изображения фантома печени (фантом Алдерсона), от частоты для трех разных значений полного количества отсчетов в изображении [4]
Так как спектр мощности шума является практически постоянным по амплитуде (белый спектр) [3, 7], то с увеличением полного количества отсчетов в изображении становится возможным отделение флуктуационного объектного спектра мощности от гладкого спектра мощности шума в области высоких частот. Это подтверждается тем, что в этом случае в изображении высокие объектные частоты могут быть извлечены из шума без излишнего усиления последнего. Таким образом, с увеличением полного числа отчетов фильтр Метца действует в соответствии с обратным фильтром (выполняет восстановление изображения от размытия из-за конечного разрешения) до более высоких частот, прежде чем начать подавление шума. Технически это достигается с помощью варьирования параметра X на базе моделирования изображений и применения метода наименьших квадратов для нахождения оптимального значения X [9]. Результаты обработки изображений, полученные с использование фильтра Метца, оказались существенно лучше (по статистическим критериям), чем с использованием девятиточечного биноминального сглаживающего фильтра (рис. 5.15).

Рис. 5.15. Изображение (500000 отсчетов) фантома печени (фантом Алдерсона) с 2-см холодным патологическим очагом при разной фильтрации: А – без фильтрации; В – девятиточечный биноминальный сглаживающий фильтр; С и D – фильтр Метца с разными методами моделирования MTF [4]

5.2. Фильтр Винера

Фильтр Винера использует оптимальный критерий в виде минимизации среднеквадратичного отклонения между фильтрованным изображением и истинным объектным изображением f(i,j). В частотном домене фильтр Винера имеет вид [10]:

(5.18)

где |N(u,v)|² и |F(u,v)|² – спектр мощности щума n(i,j) и объекта f(i,j) (см. уравнение 5.13).

Первый член в правой части уравнения (5.18) есть обратный фильтр, который доминирует на низких частотах, второй член обладает эффектом низкочастотной фильтрации, которая управляется отношением мощности спектра шума к мощности спектра объекта. Это отношение определяет, когда фильтр Винера переключается с восстановления изображения от эффекта разрешения (обратный фильтр) к подавлению шума. Член MTF в фильтре Винера предполагается стационарной функцией (т.е. инвариантной относительно положения источника и геометрии объекта), поэтому он измеряется на средней глубине.

Так как спектр мощности шума и объекта заранее не известны, то следует использовать их оценки. В работе [10] описывается методика оценки этих функций из измеренных сцинтиграмм. Основываясь на модели шума [7], спектр мощности считается независимым от частоты и равным полному числу отсчетов изображения. Оценка объектного спектра мощности проводится в следующей последовательности. Первое, спектр мощности двумерного изображения сжимается в одномерный путем усреднения по кольцевым областям в частотном прстранстве. Спектр мощности на низких частотах оценивается как разность между спектром мощности изображения и оцененным спектром мощности шума и последующим делением на среднее MTF. На высоких частотах объектный спектр мощности оценивается с помощью метода подгонки кривых, используя моель степенного закона [10]. После определения этих величин генерируется двумерная ротационно-симметричная версия фильтра и применяется к изображению. На рис. 5.16 проводится сравнение изображений костного скелета после разных видов процессинга.


Рис. 5.16. Клинические изображения костного скелета, получающиеся после разных видов фильтрации: верх слева – без фильтрации; верх справа – фильтр Баттеруорта четвертого порядка с пороговой частотой 0,4; низ слева – фильтр Метца; низ справа – фильтр Винера [4]