Физика ядерной медицины
 Скачать 9.62 Mb. Скачать 9.62 Mb.
|
Процесс ослабления γ-излученияОслабление интенсивности γ-излучения при прохождении его через среду происходит за счет взаимодействия фотонов с атомами, ядрами и электронами среды. В рассматриваемой области энергий (20 – 500 кэВ) основными видами взаимодействия являются комптоновское (точнее некогерентное) рассеяние и фотопоглощение фотонов. Для элементов, входящих в состав биологической ткани при энергии фотонов ≥ (30 – 40 кэВ), доминирующим эффектом взаимодействия является комптоновское рассеяние (см. главу 1), при котором фотон теряет часть своей энергии и отклоняется от направления первоначального движения. В то же время для элементов, входящих в состав скелета, эффект фотопоглощения играет более значимую роль, особенно в диапазоне низких энергий фотонов. В специальной геометрии, называемой геометрией узкого пучка, эффект ослабления описывается простой экспоненциальной функцией. Особенностью этой геометрии является отсутствие в пучке рассеянных фотонов, или регистрация детектором только фотонов с первоначальной энергией. Если узкий мононаправленный пучок падает на плоский срез материала толщиной x, то долю фотонов, которые не рассеются и не поглощаются в слое, можно определить экспериментально, помещая сильно коллимированный детектор фотонов на оси пучка на противоположной стороне среза (рис.6.1). Рассеянные фотоны выходят из пучка и не попадают в детектор (за исключением фотонов, рассеянных на очень малые углы). В этих условиях скорость счета C, регистрируемая детектором, связана со скоростью счета в отсутствии слоя материала Co простой формулой: 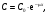 (6.1) (6.1)где μ – линейный коэффициент ослабления фотонов, зависящий от их энергии и материала (см. рис. 1.23) 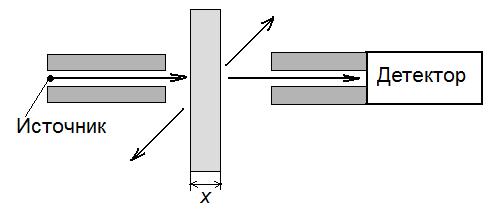 Рис. 6.1. Измерение поглощения γ-излучения в плоском срезе материала в геометрии узкого пучка Уравнение (6.1), дополненное учетом геометрического ослабления излучения, можно использовать для оценки истинного количества активности, находящегося внутри пациента, если известно расстояние x от локализации активности до поверхности кожи. Данное расстояние возможно определить поперечной гамма-камерой, ультразвуковой аппаратурой или радиографическими исследованиями. Средние значения расстояний до органов приближенно можно найти по анатомическим данным. Скорость счета конвертируется в определение активности, измеряя источник известной активности в отсутствии поглощающего вещества. Из этих измерений находится коэффициент пропорциональности k между активностью стандартного источника As и скоростью счета Cs, измеренной гамма-камерой в отсутствии ослабления: 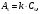 (6.2) (6.2)где k имеет размерность милликюри (или Беккерель) активности на отсчет в секунду. Отсюда активность внутри пациента равна: 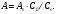 (6.3) (6.3)
В тех случаях, когда определение глубины расположения активности является непростой задачей, полезным оказывается применение метода геометрического среднего [1, 2]. В этом методе требуется, чтобы активность измерялась с противоположных направлений, например, сверху/снизу или справа/слева. Предположим, что достаточно сконцентрированная активность расположена на расстоянии x от верхней границы и на расстоянии у от нижней границы пациента с полной толщиной T = x + y (рис. 6.2). 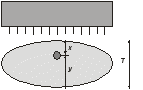 Рис. 6.2. Геометрия измерения локализованной активности гамма-камерой в однородной среде методом геометрического среднего Скорости счета гамма-камеры в верхнем Caи нижнем Cp положениях связаны с C0 формулами: 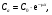 (6.4) (6.4)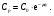 (6.5) (6.5)Перемножая (6.4) и (6.5), получаем 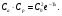 (6.6) (6.6)Откуда находим, что 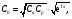 (6.7) (6.7)где член 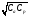 называется геометрическим средним Caи Cp. Другой член exp(Tx/2) является постоянным, его можно определить через два дополнительных измерения. Например, первое измерение: гамма-камера располагается в верхнем положении, а источник известной активности – в нижнем положении на вертикальной линии, проходящей через патологический очаг. Скорость счета, обусловленная только одним стандартным источником S, находится после корректировки на зарегистрированную скорость счета от пациента Ca. Второе измерение скорости счета S0 от стандартного источника проводится при удаленном пациенте. Отсюда значение eμT находится из выражения называется геометрическим средним Caи Cp. Другой член exp(Tx/2) является постоянным, его можно определить через два дополнительных измерения. Например, первое измерение: гамма-камера располагается в верхнем положении, а источник известной активности – в нижнем положении на вертикальной линии, проходящей через патологический очаг. Скорость счета, обусловленная только одним стандартным источником S, находится после корректировки на зарегистрированную скорость счета от пациента Ca. Второе измерение скорости счета S0 от стандартного источника проводится при удаленном пациенте. Отсюда значение eμT находится из выражения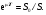 (6.8) (6.8)Окончательно, используя уравнения ((6.2). (6.3), (6.6) и (6.8)), получаем 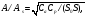 (6.9) (6.9)где Ca, Cp – скорости счета в верхнем и нижнем положении гамма-камеры, соответственно, обусловленные активностью в патологическом очаге; S – скорость счета от излучения стандартного источника, проходящего через пациента, скорректированная на вклад Ca от активности в патологическом очаге; S0 – скорость счета от стандартного источника в отсутствии пациента. До этого момента предполагалось, что пациент состоит из однородного материала с линейным коэффициентом ослабления μ. В реальности это допущение часто бывает некорректным. Тем не менее, уравнение (6.9) и в этом случае является справедливым при условии, что все измерения проводятся в геометрии узкого пучка. Другое сомнительное допущение относится к предположению о локализации активности подобно точечному источнику. Давайте рассмотрим случай, когда активность находится в объемном органе с шириной w вдоль направления, просматриваемого гамма-камерой (рис. 6.3). 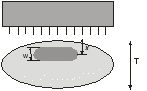 Рис. 6.3. Геометрия источника, распределенного по органу толщиной w вдоль направления, просматриваемого камерой Пусть центр органа лежит на расстоянии x от верхней поверхности пациента. Тогда поправочный фактор g должен быть применен к правой части уравнений (6.4) и (6.5): 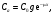 (6.10) (6.10)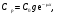 (6.11) (6.11)где 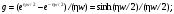 (6.12) (6.12)η – коэффициент ослабления органа; μ – эффективный коэффициент ослабления оставшейся части тела. Если для калибровки используется стандартный источник известной активности, то формула (6.9) переходит в следующую: 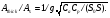 (6.13) (6.13)Анализ показывает, что величина g медленно меняется с изменением w (рис. 6.4), поэтому w необходимо знать приближенно. Учет фоновой активности, находящейся в тканях, окружающих исследуемый орган, обычно бывает существенным, но получить высокую точность этого учета проблематично. Для решения проблемы в литературе предложено ряд методов [4, 5]. Традиционно счет от районов, примыкающих к области интереса, вычитается на основе число отсчетов на пиксель. Эта методика обычно имеет тенденцию к избыточной коррекции, когда фоновая активность не простирается в орган. Более точный результат определения скорости счета от фоновой активности (b') получается при использовании следующей формулы: 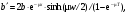 (6.14) (6.14)где b – кажущаяся скорость счета фона, основанная на простом измерении фона от района интереса. 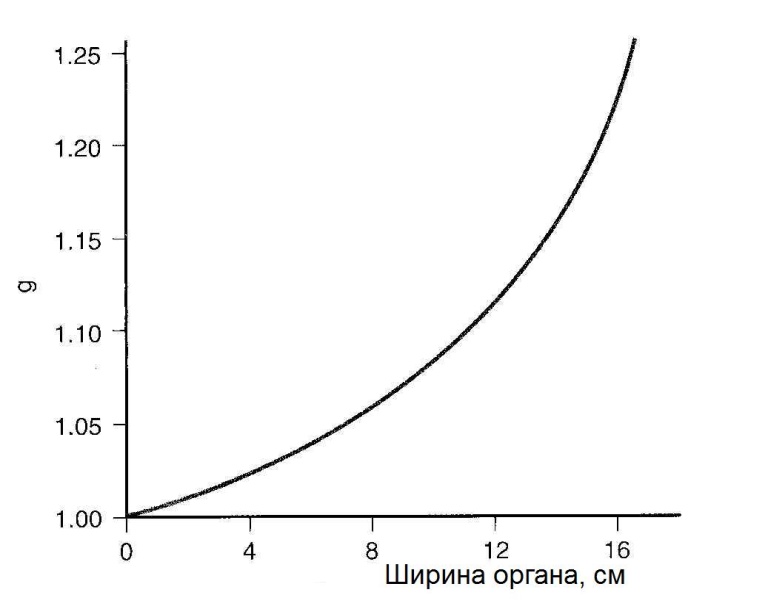 Рис. 6.4. Зависимость фактора g от толщины органа для 140-кэВ фотонов в воде [3] |
