дипломная. Формирование логического мышления младших школьников при изучения нумерации многозначных чисел
 Скачать 472 Kb. Скачать 472 Kb.
|
|
2.2 Формирующий эксперимент. На втором этапе нами была проведена формирующая работа по развитию у учащихся нумерации многозначных чисел. В начальной школе большое место должно быть отведено к обучению операциям направленных на развитие логического мышления логического мышления: анализу, синтезу, сравнению, классификации, обобщению. учащихся 3«В» класса» МБОУ «СОШ №1» Гудермеский район п. Нижний Нойбер. Рассмотрели систему упражнений по математике УМК «Начальная школа XXI века», автор В.Н.Рудницкая, направленные на формирование этих операций. Провели проверочные работы, математические диктанты, устные работы: Задания, направленные на развитие анализа и синтеза: 1. Соединение элементов в единое целое: Выбери детали, из которых можно сложить круг. 2. Поиск различных признаков предмета: Сколько ломаных из двух звеньев можно найти на рисунке? Найди из 3-х звеньев, из 4 –х звеньев. 3. Узнавание или составление объекта по заданным признакам: а) В каждой тройке запиши числа, соседние с данным: 207, … , …. …. , 105, …. …. , …. , 546 б) Найди закономерность и напиши ещё два числа в каждом ряду: 85, 97, 109, 121, 133, … , … 901, 802, 703, 604, … , … 5, 6, 8, 11, 15, 20, … , … в) Рассмотри краткую запись задачи. Составь и реши её.    I -307 кг I -307 кг II - ? на 48 кг больше, чем ? кг II - ? на 48 кг больше, чем ? кгIII -285 кг г) Запиши в порядке увеличения: 72, 722, 277, 227, 222, 727, 777 д) Запиши в порядке убывания: 95, 995, 559, 59, 595, 999, 958, 599 Устная работа: увеличить число 39 в 100 (1 000) раз; уменьшить число 3 010 000 в 100 (1 000) раз; прочитать число 2 456 756; 3 456 456; 2 000 000; сколько сотен (тысяч) в числе 50 895? Сколько цифр в десятичной системе счисления? Математический диктант: Выписать разрядные числа: 1 дес., 900, 320, 2 сот., 1 000, 2 тыс., 20, 735, 2 млн. Сколько слов надо запомнить, чтобы назвать все числа от 1 до 10, 100, 1 000? Сколько цифр в десятичной системе счисления? Записать цифрами число: а) 4 млн.607 тыс., б) указать, единицы каких разрядов и классов отсутствуют в данном числе. А также проводилась дидактическая игра “Допишите пропущенные цифры” Цель: отработать навык сложения многозначных чисел. Содержание игры. Перед началом игры учитель на доске решает пример на сложение с пропущенными цифрами. Затем к доске выходят пять - шесть человек и под руководством учителя решают подобные примеры. Только после такой предварительной подготовки учащимся можно предложить решать такие примеры самостоятельно. ? 5 4 3 ? 2 ? 7 4 ? 6 ? 5 ? ? ? 3 6 ? 1 ? 4 ? 2 ? 3 ? ? 7 ? 3 ? 7 1 ? 6 ? 4    4 6 8 7 9 9 7 9 6 9 1 8 0 0 3 7 9 8 7 4 6 8 7 9 9 7 9 6 9 1 8 0 0 3 7 9 8 7 предложенные примеры должны быть решены учащимися за определённый срок. Кто решил правильно большее количество примеров за этот срок - выигрывает. Можно также организовать соревнование между двумя - тремя учениками. Выигрывает тот, кто верно и быстрее решил все примеры. Примечание. Примеры с пропущенными цифрами можно дать учащимся и на другие арифметические действия. Таким образом, проводимые упражнения вызывали у детей интерес - активно работали на уроках, стремились прийти к правильному результату. 2.3 Контрольный этап эксперимента. Повторно провели групповое обследование уровня развития логического мышления учащихся 3 «В» МБОУ «СОШ №1» Гудермеский район п. Нижний Нойбер Детям раздали карточки (количество-5), на которых написано - 5 заданий Карточка №1 Логические задачи. Примеры логических задач связанных с математикой способствующих развитию логического мышления: 1.На веревке завязали пять узлов. На сколько частей эти узлы разделили веревку? 2.Чтобы распилить доску на несколько частей, ученик сделал на ней шесть отметок. На сколько частей ученик распилит доску? 3. По улице идут два сына и два отца. Всего три человека. Может ли так быть? 4. Коля ростом выше Андрея, но ниже Сережи. Кто выше Андрей или Сережа? 5.Чтобы сварить 1 кг мяса требуется 1 час. За сколько часов сварится 2 кг мяса? Карточка №2 2. Сравни числа, поставив знак < или >. 41989 ... 42012 399917 ... 399971 53010 …50003 43758…43759 48083…47999 Карточка №3 3. Реши примеры: 500000 - 290737 = 800000 – 605409= 737246 + 54337= 516739 + 175152= 893456+137863= Карточка №4 4. Реши примеры: 698 : 34 = 2744 : 56= 123 968 : 64= 69 384 :28 = 28320:24 = Карточка №5 4. Реши примеры:
Качественная оценка решения задач Успешное решение ребёнком всех задач позволяет говорить об относительно высоком уровне теоретического и практического способа решения заданий. Низкий уровень. Ученик не способен самостоятельно проанализировать содержание задачи. Он может выделить условия, вопрос задачи только при помощи наводящих вопросов учителя. Соответственно, он не может самостоятельно наметить и составить план решения, а значит, не способен самостоятельно решить задачу и найти ответ. Средний уровень. Ученик может самостоятельно выделить условия и вопрос задачи, определить, что в задаче известно и что нужно найти. Намечает, не всегда правильно, план решения задачи. Далеко не всегда доводит его до конца. Высокий уровень. Ученик быстро и правильно анализирует задачу, составляет план решения, записывает решение и ответ. Проводит проверку ответа задачи, тем самым проявляя самоконтроль. Высокий уровень - «В»- (1-25 заданий) Средний уровень – «С»-(1-20 заданий) Низкий уровень - «Н»-(1-15 заданий) Таблица 1 . Диагностика уровня развития логического мышления учащихся 3 «В»
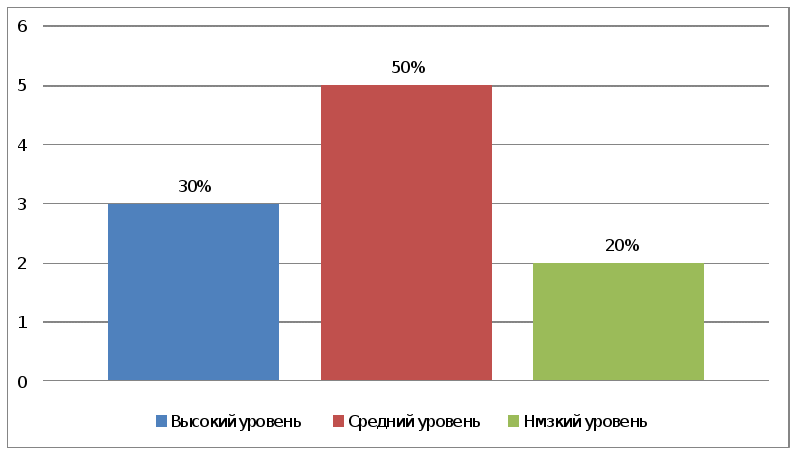 При обработке полученных ответов каждая задача(карта-5заданий), в зависимости от того, верно или неверно она решена, отмечалась («+» или « - »). Пользуясь данными этой таблицы, можно легко подсчитать количество детей, которые решили определённое число задач правильно. Контрольный этап показал следующие результаты: - высокий уровень – выполнены 1- 25 - заданий, количество - 3ч, качество выполненного задания в процентах - 30% -средний уровень – выполнено от 1-20 заданий, количество - 5ч, качество выполненного задания(количество учащихся) в процентах - 50% - низкий уровень – выполнено1- 15 заданий, количество - 2ч, качество выполненного задания (количество учащихся) в процентах 20%. Таким образом мы сделали вывод, что итоговая диагностика показала позитивные изменения в решении задач на логическое мышление. Если вначале исследования преобладали средний и низкий уровни умения решать задачи, то на контрольном этапе количество учащихся, повысивших свой уровень со среднего на высокий (от 0 до 3ч). Количество учащихся, повысивших свой уровень с низкого на средний (с 6 до 2ч). Формирование логического мышления - важнейшая составная часть педагогического процесса. Помочь учащимся проявить свои способности, развить инициативу, самостоятельность, творческий потенциал - одна из основных задач современной школы. Успешная реализация этой задачи во многом зависит от сформированности у учащихся познавательных интересов. Для развития логического мышления младших школьников, на формирующем этапе решали задачи на сравнение, на выделение существенных и несущественных признаков, задания с выбором ответа, на арифметические вычисления, что способствовало хорошему результату на контрольном этапе. Если на констатирующем этапе с задачами на логическое мышление справились-2ч., то на контрольном этапе с этими же заданиями справились-7человек. Таким образом, ученики в основной своей массе умеют анализировать задачу, владеют арифметическими действиями. Также ученики показали средний уровень сформированности понятий «взаимосвязи компонентов и результатов действия умножения и деления». Систематически использование дидактических игр повышает качество процесса обучения младших школьников, стимулирует активность каждого ребенка, что получило подтверждение наше предположение «использования на уроках математики в 4«В» классе специальных дидактических игр, будет способствовать развитию логического мышления у младших школьников» ЗАКЛЮЧЕНИЕ Проведенное нами теоретическое и экспериментальное исследование показало эффективность условий развития логического мышления и обосновало справедливость предложенной системы работы. Рассмотренные теоретические аспекты развития логического мышления на основе анализа психолого-педагогической, методической и учебной литературы по проблеме исследования позволили нам выявить особенности развития логического мышления детей младшего школьного возраста. Уместно считать данный возраст наиболее благоприятным для развития логического мышления. Были обоснованы условия развития логического мышления младших школьников на уроках математики: организационные, психолого-педагогические, методические. Также подобран комплекс специальных заданий, направленный на развитие логического мышления на уроках математики для младших школьников. Данное исследование позволило нам выявить педагогические условия повышения качества математической подготовки младших школьников посредством использования логических приемов мышления на уроках математики: выделение существенного, сравнения, обобщения, классификации. Подобранный комплекс заданий по формированию логических приемов мышления у младших школьников существенно повлиял на качество математической подготовки в экспериментальном классе у младших школьников. Таким образом, гипотеза экспериментально подтверждена. Экспериментально доказана эффективность созданных нами условий по развитию логического мышления младших школьников и специального комплекса заданий математического характера. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
