дипломная. Формирование логического мышления младших школьников при изучения нумерации многозначных чисел
 Скачать 472 Kb. Скачать 472 Kb.
|
Методика изучения нумерации многозначных чисел младшими школьникамиПри характеристике содержания и системы построения начального курса математики говорилось, что работа, направленная на формирование у детей понятия о числе и арифметических действиях, ведется в течение всех трех лет начального обучения и составляет основу всего курса. Программа предусматривает постепенное расширение области рассматриваемых чисел. Концентризм в построении программы неразрывно связан с особенностями десятичной системы счисления и нумерации многозначных чисел. В качестве первого такого концентра выделен "Десяток". При изучении этой темы дети знакомятся с первыми десятью числами натурального ряда и действиями сложения и вычитания в этих пределах. Уже на этом весьма ограниченном числовом материале рассматриваются многие вопросы, с которыми в дальнейшем учащиеся будут встречаться при каждом новом расширении области чисел. Так, именно на этом этапе обучения учащиеся должны осознать количественное и порядковое значение числа. Они должны научиться пользоваться усвоенным ими отрезком натурального ряда чисел для получения ответа на вопрос, сколько элементов входит в состав предложенного им множества, понять, что с помощью той же числовой последовательности можно расположить элементы этого множества в определенном порядке, перенумеровав их. На примере первых десяти чисел натурального ряда дети знакомятся с принципами его построения. Они осознают и усваивают, что для получения числа, следующего за данным, достаточно прибавить единицу к данному числу и что поэтому числа в натуральном ряду возрастают (каждое число ряда больше всех чисел, встречающихся при счете раньше этого числа, и меньше любого числа, которое называется при счете после него). Эти знания они применяют для сравнения чисел. Они узнают далее что каждое число (кроме единицы) может быть представлено в виде суммы двух или нескольких слагаемых. Так, переходя к рассмотрению чисел в пределах 100, дети впервые встречаются с тем фактом, что десять единиц образуют новую счетную единицу - десяток. Они узнают, что названия чисел, больших 10, образуются уже с использованием названий, принятых для первых десяти чисел (один-на-дцать, две-на-дцать, два-дцать один и т.д.), что запись чисел в пределах 100 производится с использованием тех же самых десяти цифр, но с помощью двух цифр, значение которых зависит от места, которое занимает цифра в записи. Здесь впервые дети встречаются с понятием разрядных слагаемых и учатся представлять число в виде суммы его разрядных слагаемых. В неразрывной связи с этим изучаются и соответствующие случаи сложения и вычитания (вида 20 + 7, 27 - 7, 27 - 20). Рассмотрение этих вопросов связывается с введением новой единицы измерения - дециметра. Весьма полезным оказывается при этом провести аналогию между получением двузначных чисел с помощью счета десятков и единиц и измерением отрезка сначала с помощью откладывания дециметра, а затем для измерения оставшейся части отрезка, меньшей дециметра, - с помощью откладывания сантиметра. (Например, 2 десятка и 3 единицы составляют 23 единицы, а 2 дм и 3 см - 23 см) Каждое дальнейшее расширение области чисел, как правило, всегда связывается с введением новых единиц измерения величин и установления соотношения между ними. Это создает условия, необходимые для того, чтобы подмеченная аналогия в получении чисел при счете и при измерении могла быть в дальнейшем использована при рассмотрении действий с именованными числами. Каждый раз рассматриваются новые случаи действий, основанные на знании десятичного состава чисел. Выделение концентра "Тысяча" дает возможность не только закрепить все приобретенные ранее знания нумераций, но и познакомить детей с новой счетной единицей - сотней. При этом важно показать детям общий принцип образования новых счетных единиц: 10 единиц образуют новую единицу счета - десяток, а 10 десятков - новую счетную единицу - сотню. Уже здесь можно сказать детям, что и дальше, при образовании новых чисел, 10 единиц одного разряда (сотен) образуют единицу следующего разряда - тысячу. Таким образом подготавливается почва для ознакомления детей с принципом десятичной системы счисления, который выступит в еще более общей форме при рассмотрении темы "Многозначные числа". Здесь новым будет усвоение понятия класса, принципа устной и письменной нумерации чисел II и III классов. Итак, выделение концентров в начальном курсе математики дает возможность неоднократно возвращаться к рассмотрению основных вопросов, связанных с особенностями десятичной системы счисления, устной и письменной нумерации чисел, закрепляя знания детей. Это, как было только, что показано, создает условия и для формирования соответствующих обобщений. Благодаря концентрическому построению программы возникает также возможность рассредоточить трудности, в связи с чем в процессе обучения можно значительно увеличить долю самостоятельного участия детей в рассмотрении тех вопросов нумерации, которые при расширении области чисел могут быть ими усвоены на основе "переноса" приобретенных ранее знании. Отметим здесь и другие принципиальные моменты, которые должны учитываться в работе над нумерацией, о какой бы области чисел ни шла речь. Названия чисел, особенности образования соответствующих числительных дети воспринимают не только со слов учителя. Огромную роль играет при этом интуиция (чутье), основанная на владении родным языком. Дети легко самостоятельно (а иногда лишь при небольшом намеке со стороны учителя) подмечают принцип образования названий чисел и сами догадываются, как будут называться следующие числа, если только дать им для примера два-три аналогичных названия. Например: "двадцать один", "двадцать два"... (Трудности возникают только в таких случаях как "сорок", "пятьдесят", "девяносто", которые приходится специально оговаривать) Учитывая это обстоятельство, в процессе обучения нужно стремиться к тому, чтобы усвоение последовательности соответствующих числительных всегда несколько опережало ту область чисел, которая рассматривается в данный момент более основательно. Так, приступая к изучению чисел первого десятка, дети должны уже к этому времени более или менее уверенно знать названия этих чисел, порядок их следования при счете. Изучая тему "Десяток", полезно уже заранее в устных упражнениях использовать счет предметов и в тех случаях, когда он выходит за пределы 10. Это не значит, что нужно требовать от всех детей прочного усвоения соответствующей последовательности чисел. Пусть ее усвоят не все, пусть некоторые еще будут иногда ошибаться, воспроизводя ее. Важно, чтобы она была им знакома к тому времени, когда они приступят к изучению темы "Нумерация чисел в пределах ста". Что это дает? Во-первых, при этом легче усваивается устная нумерация на уроках, специально посвященных этим вопросам. Во-вторых, знание названий чисел, к рассмотрению которых дети приступают (даже если и не все эти названия усвоены одинаково уверенно всеми учениками), позволяет учителю опереться на анализ самих этих названий (числительных) для раскрытия принципа образования чисел, их состава из разрядных слагаемых. Например, если ученик знает, что после двадцати идет число двадцать один, затем двадцать два и т.д., то достаточно обратить его внимание на то, что "-дцать" в названии числа двадцать означает "десять" ("десяток"), как десятичный состав любого из чисел в пределах 100 становится понятным по одному его названию: тридцать четыре - 3 десятка и 4 единицы и т.п. (исключение составят только числа от 40 до 49 и от 90 до 99). Наконец, в-третьих, некоторое забегание вперед в усвоении счета предметов за пределом изучаемой области чисел помогает сформировать у детей правильное представление о том, что всегда можно назвать число, которое больше самого большого из известных уже к этому времени чисел. Дети перестают в этих условиях думать, что, например, на числе 10 (или 100, или 1000) счет обрывается. Такое забегание вперед создает, кроме того, условия для переноса изученных операций (в частности, операции счета предметов, приема присчитывания по 1 и др.) на несколько расширенную область чисел. Это очень важно в качестве психологической подготовки детей к работе с большими числами. Далее, как это было показано выше, концентризм в изучении нумерации создает такие условия, при которых в каждой новой теме дети вновь возвращаются к рассмотрению всех тех вопросов, которые рассматривались раньше. Это обязывает особенно внимательно следить за тем, чтобы не нарушить одно из основных педагогических требований - не объяснять как новое то, что уже известно, всячески стимулировать самостоятельное перенесение детьми приобретенных знаний на рассмотрение новых чисел. Отрабатывая усвоение ряда чисел, необходимо, поэтому включать соответствующие упражнения наряду с выделением наиболее трудных пунктов этого ряда, связанных с переходом к новой счетной единице (97, 98, 99..., 998, 999,. .) или с введением числительного, представляющего собой исключение из общего правила (например, "сорок"). В результате изучения нумерации чисел дети должны не только усвоить соответствующие общие положения, но и овладеть важнейшими умениями и навыками. Поэтому в учебниках математики для начальных классов намечена система упражнений, необходимых для сознательного усвоения детьми всех основных вопросов, связанных с изучением нумерации. Для формирования прочных навыков в данном случае необходимо такие упражнения давать специально почти на каждом уроке, составляя упражнения по образцу данных в учебнике и включая их небольшими порциями на уроках, следующих за изучением данной темы (по 2-3 упражнения). Изучение нумерации, как известно, является основой работы над арифметическими действиями. Здесь применяются все знания, умения и навыки, которые дети получают, знакомясь с десятичной системой счисления и нумерацией. Поэтому в ходе изучения действий происходит естественное закрепление и совершенствование приобретенных знаний. Таким образом, сделаем вывод, что при теоретическом исследование проблемы развития логического мышления детей на уроках математики в начальной школе приведенное в главе I, позволило сформулировать следующие выводы: Мышление – это процесс познавательной деятельности индивида, характеризующийся обобщенным и опосредствованным отражением действительности. Логическое мышление определяется как «вид мышления, сущность которого заключается в оперировании понятиями, суждениями и умозаключениями с использованием законов логики». Логика мышления не дана человеку от рождения. Ею он овладевает в процессе жизни, в обучении. Поэтому необходимо создавать такие условия, которые способствовали бы наиболее эффективному развитию логического мышления у детей младшего школьного возраста. Анализ научной литературы по проблеме исследования позволил нам уточнить условия, способствующие, на наш взгляд, развитию логического мышления младших школьников: организационные, психолого-педагогические, методические. Возникает необходимость подобрать специальный комплекс заданий по математике, направленный на развитие логического мышления младших школьников. Изобретение десятичной системы счисления относится к главным достижениям человеческой мысли. Без нее вряд ли могла существовать, а тем более возникнуть современная техника и наука вообще. Одним из важных моментов в работе над нумерацией является закрепление последовательности и свойств натурального ряда чисел (если к числу прибавим 1, то получим следующее за ним число, а если вычтем 1, то - предшествующее. Уроки математики могут и должны быть использованы в целях формирования у детей начатков научного мировоззрения. Этому способствует укрепление связи обучения с жизнью, нужно довести до сознания детей связь математики с практикой. Для этого необходимо, прежде всего, систематически развивать у детей самостоятельность, постепенно усиливая в процессе обучения требования к их самостоятельной работе, но, соблюдая при этом такую меру трудности, при которой предлагаемые вопросы и задания, хотя и требовали бы определенных усилий от ребенка, оставались бы посильными для него. Основой для изучения нумерации многозначных чисел является хорошее знание нумерации чисел в пределах 1000. Выполняя конкретные упражнения, учащиеся вспоминают, как образуется число, непосредственно следующее при счете за данным, а также число, предшествующее данному при счете; повторяют образование чисел из сотен, десятков и единиц и учатся откладывать на счетах однозначные, двузначные и трехзначные числа. На этом знакомом детям материале вводится новые понятия - понятия разряда и класса. Чтобы дети быстрее запомнили новые термины, полезно вывесить в классе нумерационную таблицу и пользоваться этим пособием на всех уроках повторения. ГЛАВА 2. ОПЫТНО-ЭКСПЕРИМЕНТАЛЬНАЯ РАБОТА ПО ФОРМИРОВАНИЮ ЛОГИЧЕСКОГО МЫШЛЕНИЯ МЛАДШИХ ШКОЛЬНИКОВ ПРИ ИЗУЧЕНИИ МНОГОЗНАЧНЫХ ЧИСЕЛ. Опытно-экспериментальная работа по развитию логического мышления младших школьников при изучении многозначных чисел проводилась в 3«В» классе МБОУ «СОШ №1» Гудермеский район п. Нижний Нойбер. В эксперименте принимали 10 учащихся, в целом класс со средней успеваемостью. I этап - констатирующий. II этап - формирующий. III этап - контрольный. Цель эксперимента: выявить, знают ли дети нумерацию многозначных числел и могут ли их применять. Задачи: 1) выбрать исследовательские методы для экспериментального класса; 2) провести исследование и апробировать результаты. Рассмотрим уровень развития логического мышления учащихся на констатирующем этапе исследования в котором была проведена самостоятельная работа. Карточка №1 Логические задачи. Примеры логических задач связанных с математикой способствующих развитию логического мышления: 1.На веревке завязали пять узлов. На сколько частей эти узлы разделили веревку? 2.Чтобы распилить доску на несколько частей, ученик сделал на ней шесть отметок. На сколько частей ученик распилит доску? 3. По улице идут два сына и два отца. Всего три человека. Может ли так быть? 4. Коля ростом выше Андрея, но ниже Сережи. Кто выше Андрей или Сережа? 5.Чтобы сварить 1 кг мяса требуется 1 час. За сколько часов сварится 2 кг мяса? Карточка №2 2. Сравни числа, поставив знак < или >. 419 ... 42012 ... 399 5301 …5000…4379 4808…4798 Карточка №3 3. Реши примеры: 500000 - 290737 = 800000 – 605409= 737246 + 54337= 516739 + 175152= 893456+137863= Карточка №4 4. сравни числа и найди лишнее в каждом ряду (зачеркни его) 2,3,6,7,11,8 18,12,3,29,45,28 10,20,30,36,40,50 Карточка №5 5. Заполни пропуски. 1 дм 8 см = ___ см 16 см = __ дм __ см Качественная оценка решения задач Успешное решение ребёнком всех задач позволяет говорить об относительно высоком уровне теоретического и практического способа решения заданий. Низкий уровень. Ученик не способен самостоятельно проанализировать содержание задачи. Он может выделить условия, вопрос задачи только при помощи наводящих вопросов учителя. Соответственно, он не может самостоятельно наметить и составить план решения, а значит, не способен самостоятельно решить задачу и найти ответ. Средний уровень. Ученик может самостоятельно выделить условия и вопрос задачи, определить, что в задаче известно и что нужно найти. Намечает, не всегда правильно, план решения задачи. Далеко не всегда доводит его до конца. Высокий уровень. Ученик быстро и правильно анализирует задачу, составляет план решения, записывает решение и ответ. Проводит проверку ответа задачи, тем самым проявляя самоконтроль. Высокий уровень - «В»- (1-25 заданий) Средний уровень – «С»-(1-20 заданий) Низкий уровень - «Н»-(1-15 заданий) Таблица 1. Диагностика уровня развития логического мышления учащихся 3 «В»
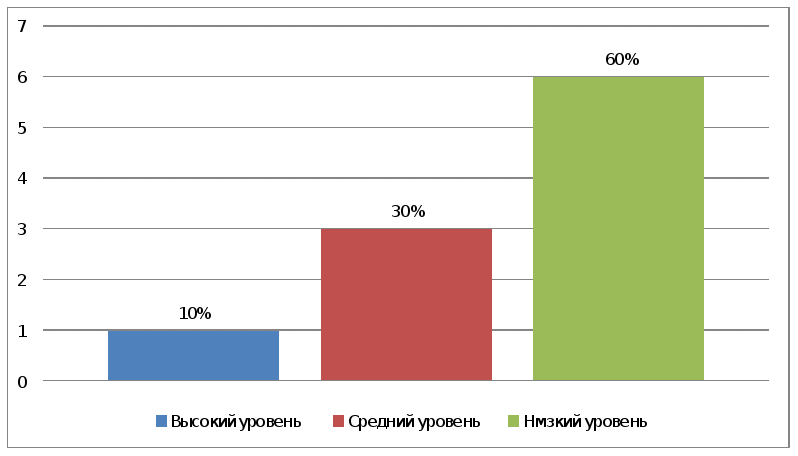 Результаты констатирующего эксперимента наглядно представлено на рис.1 Таким образом, на основе проведенной самостоятельной работы можно сделать вывод о том, что высокий уровень – выполнены 1-25 заданий, количество - 1ч, качество выполненного задания в процентах - 10%, средний уровень – выполнено от 1-20 заданий, количество - 3ч, качество выполненного задания(количество учащихся) в процентах - 30%, низкий уровень – выполнено 15 заданий, количество - 6ч, качество выполненного задания (количество учащихся) в процентах 60% Проанализировав результаты самостоятельной работы и определив уровень развития ученики в основной своей массе не умеют решать задачи на логическое мышлении, допускают ошибки в арифметических вычислениях. Для подтверждения гипотезы на втором этапе мы подобрали логические задания на выяснение закономерности, сходства и различия примеров, которые будут способствовать эффективному развитию логического мышления младших школьников при изучении многозначных чисел. И разработали проект, где включает конспекты уроков по математике с логическими заданиями при изучении нумерации многозначных чисел . | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
