математическая грамотность. Математическая грамотность. Формрование функциональной грамотности математическая грамотность
 Скачать 2.14 Mb. Скачать 2.14 Mb.
|
|
ФОРМРОВАНИЕ ФУНКЦИОНАЛЬНОЙ ГРАМОТНОСТИ МАТЕМАТИЧЕСКАЯ ГРАМОТНОСТЬ Математическая грамотность – это способность человека мыслить математически, формулировать, применять и интерпретировать математику для решения задач в разнообразных практических контекстах. Она включает в себя понятия, процедуры и факты, а также инструменты для описания, объяснения и предсказания явлений. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые должны принимать конструктивные, активные и размышляющие граждане в 21 веке. В определении математической грамотности особое внимание уделяется использованию математики для решения практических задач в различных контекстах. Учителя математики наряду с формированием предметных знаний и умений обеспечивают развитие у обучающихся математической грамотности. В дальнейшем это умение будет способствовать успешной социализации выпускника школы во взрослой жизни. Модель математической грамотности  Мониторинг формирования математической грамотности Обучающимся предлагаются не типичные учебные задачи, а близкие к реальным проблемные ситуации, представленные в некотором контексте и разрешаемые доступными учащемуся средствами математики Основа организации исследования математической грамотности включает три структурных компонента: − контекст, в котором представлена проблема; − содержание математического образования, которое используется в заданиях; − мыслительная деятельность, необходимая для того, чтобы связать контекст, в котором представлена проблема, с математическим содержанием, необходимым для её решения Контексты заданий личная жизнь образование/профессиональная деятельность общественная жизнь научная деятельность Математическое содержание заданий пространство и форма – задания, относящиеся к пространственным и плоским геометрическим формам и отношениям, т.е. к геометрическому материалу; изменение и зависимости – задания, связанные с математическим описанием зависимости между переменными в различных процессах, т.е. с алгебраическим материалом; количество – задания, связанные с числами и отношениями между ними, в программах по математике этот материал чаще всего относится к курсу арифметики; неопределённость и данные – задания охватывают вероятностные и статистические явления и зависимости, которые являются предметом изучения разделов статистики и вероятности Мыслительная деятельность направлена на то, чтобы ученик мог: формулировать ситуацию на языке математики; применять математические понятия, факты, процедуры размышления; интерпретировать, использовать и оценивать математические результаты. Очевидно, что каждый из этих мыслительных процессов опирается на математические рассуждения PISA выделяет 6 уровней функциональной грамотности Уровень 6 (нижняя граница в баллах – 669,30) Уровень 5 (границы в баллах: 606,99 – 669,30) Уровень 4 (границы в баллах: 544,68 – 606,99) Уровень 3 (границы в баллах: 482,38 – 544,68) Уровень 2 (границы в баллах: 420,07 – 482,38) Уровень 1 (границы в баллах: 357,77 – 420,07) Уровень ниже 1 (верхняя граница в баллах 357,77  Развивать математическую грамотность надо постепенно, начиная с 5 класса. Регулярно включать в ход урока задания на «изменение и зависимости», «пространство и форма», «неопределенность», «количественные рассуждения» Эти задания можно использовать по усмотрению учителя: Как игровой момент на уроке; Как проблемный элемент в начале урока; Как задание – «толчок» к созданию гипотезы для исследовательского проекта; Как задание для смены деятельности на уроке; Как модель реальной жизненной ситуации, иллюстрирующей необходимость изучения какого либо понятия на уроке; Как задание, устанавливающее межпредметные связи в процессе обучения; Некоторые задания заставят сформулировать свою точку зрения и найти аргументы для её защиты; Можно собрать задания одного типа и провести урок в соответствии с какой то образовательной технологией; Можно все задачи объединить в группы и создать свой элективный курс по развитию математического мышления; Задания такого типа можно включать в школьные олимпиады, математические викторины Поэтапное развитие различных умений, составляющих основу математической грамотности 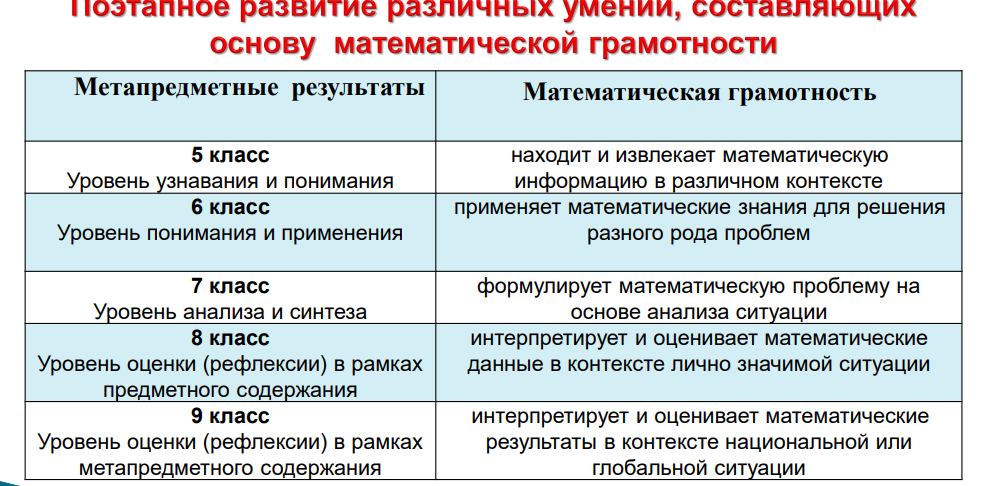 Концептуальные рамки оценки математической грамотности Принятое определение математической грамотности повлекло за собой разработку особого инструментария исследования: учащимся предлагаются не типичные учебные задачи, характерные для традиционных систем обучения и мониторинговых исследований математической подготовки, а близкие к реальным проблемные ситуации, представленные в некотором контексте и разрешаемые доступными учащемуся средствами математики.       С 2019 – 2020 года в ОГЭ включена практико-ориентированная задача, что повлекло большие затраты времени при подготовке к ОГЭ. Каждый год типов таких задач становится все больше. Наличие объемного текста негативно сказывается на выполнении математической задачи.   Учащиеся, овладевшие математической грамотностью, способны: - распознавать проблемы, которые возникают в окружающей действительности и могут быть решены средствами математики; - формулировать эти проблемы на языке математики; - решать проблемы, используя математические факты и методы; - анализировать использованные методы решения; - интерпретировать полученные результаты с учетом поставленной проблемы; - формулировать и записывать результаты решения. |
